В.Н. Дурова М.И. Зайцева В.Н. Макаров
ТЕОРИЯ МНОЖЕСТВ.
МАТЕМАТИЧЕСКАЯ ЛОГИКА
Учебное пособие
Воронеж 2006
Воронежский государственный технический
университет
В.Н. Дурова М.И. Зайцева В.Н. Макаров
ТЕОРИЯ МНОЖЕСТВ.
МАТЕМАТИЧЕСКАЯ ЛОГИКА
Утверждено Редакционно-издательским советом
университета в качестве учебного пособия
Воронеж 2006
Введение
Пособие написано в соответствии с образовательным стандартом специальностей 160201 «Самолето-и вертолетостроение,130501 «Проектирование, сооружение и эксплуатация газонефтепроводов и газонефтехранилищ», 220501 «Управление качеством». Понятия и методы теории множеств и математической логики в связи с компьютеризацией образования должны занимать существенное место в математической подготовке инженера. Большинство вопросов указанных разделов предназначено для самостоятельного изучения студентами. С целью облегчения самостоятельной работы студентов изложение материала сопровождается большим количеством подробно решенных примеров. Приводятся примеры для самостоятельного решения.
1. Элементы теории множеств
1.1 Множества. Основные понятия
Различают аксиоматическую теорию множеств и элементарную теорию множеств. В дальнейшем рассматривается элементарная теория множеств.
Понятие множества и элемента множества принадлежат к числу неопределяемых явно понятий математики, таких, как, например, число, точка и прямая.
Под множеством понимают набор, совокупность каких-либо объектов, обладающих общим характеристическим свойством.
Объекты, из которых составлено множество, называются его элементами.
Понятие множества часто употребляется в повседневной жизни и для него имеется много общеизвестных синонимов (класс, совокупность, толпа, стая), некоторые, из которых имеют специфический оттенок.
Множества обозначаются заглавными буквами латинского алфавита, его элементы – малыми буквами.
Примеры.
1. Множество натуральных чисел (N): 1, 2, 3, …
2. Множество простых чисел (P): 2, 3, 5, 7, 11, …
3. Множество целых чисел (Z): … -2, -1, 0, 1, 2, …
4. Множество действительных чисел (R).
5. Множество комплексных чисел (С).
6. Множество матриц размера m x n;
7. Множество векторов в
и
т. д.
Принадлежность элемента x множеству М обозначается xМ. В противном случае xМ.
Как правило, считается, что все элементы множества различны. Множество с повторяющимися элементами называется мультимножеством. Мультимножества играют важную роль в комбинаторике. В данном разделе будем рассматривать только множества с различными элементами.
, как объекты, могут быть элементами других множеств. Множество, элементами которого являются множества, обычно называются классом или семейством.
Например, множество групп студентов состоит из элементов (групп), которые, в свою очередь, состоят из студентов.
С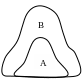
емейства
множеств обычно обозначаются заглавными
«рукописными» буквами латинского
алфавита.
Множество, не содержащее ни одного элемента, называется пустым и обозначается .
Множество, состоящее из конечного числа элементов, называется конечным, в.противном случае Рис.1
– беcконечным.
Например, множества N, R – бесконечные множества.
Число элементов в конечном множестве М называется его мощностью и обозначается М= n, если множество М содержит n элементов.
Мощность пустого множества равна 0: = 0.
Для произвольных множеств А и В определяются два типа отношений – отношение включения и отношения равенства.
Множество А называется подмножеством множества В, если каждый элемент из А является элементом В.
Обозначаются
(А включено в В). В частности, А
и В могут совпадать, поэтому
называется также отношением не строгого
включения.
Очевидные свойства операции включения:
.
Если
и
, то говорят, что А есть собственное
подмножество В и обозначают
.
Отношение между множествами в этом
случае называется отношением строгого
включения. В этом случае
и
.
Обычно элементы всех множеств берутся из некоторого одного, достаточно широкого множества U (, Е) (своего для каждого случая), которое называется универсальным (основным) множеством (или универсумом).
Пустое множество, по определению, является подмножеством всякого множества.
Пустое множество и само множество U называются несобственными подмножествами. Все остальные подмножества множества U называются собственными.
Два определения равенства множеств:
1. Множества А и В равны (А=В), если их элементы совпадают.
2. Множества А и В равны, если
и
.
Очевидно, что для любых множеств А, В и С справедливы соотношения:
Совокупность всех подмножеств множества
А называется его булеаном или
множеством-степенью и обозначается
P(А)
или
.
Пример. Пусть А={1,2,3}.
Тогда P(А)={,{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}}.