Учебное пособие 1699

Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

где якобиан преобразования равен

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

1.81 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 225 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

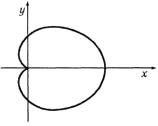
в) Поскольку кардиоида симметрична относительно полярной оси (рис. 1.30), то yc = 0 .

Рис. 1.30

Масса пластинки и статический момент относительно оси Оу находятся по формулам

m = ∫∫dxdy; my = ∫∫xdxdy.

													S										S
Переходя к полярным координатам
									x = ρ cosϕ; y = ρsinϕ ,
будем иметь															a(1+cosϕ)
											π				a(1+cosϕ)												π	(1+cosϕ)2 dϕ =
m = ∫∫ρd ρdϕ = 2∫dϕ																		∫			ρd ρ = a2 ∫							(1+cosϕ)2 dϕ =
		S								0								0									0
	2										1						1				2			π			3			2
	2										1						1				2			π			3			2
= a		1+			2sinϕ			+					ϕ		+				sin			ϕ		=				πa				.
= a		1+			2sinϕ			+					ϕ		+		2		sin			ϕ		=			2	πa				.
											2						2							0			2
																				π				0	a(1+cosϕ)
																				π					a(1+cosϕ)
my			= ∫∫ρ cosϕρd ρdϕ = 2∫cosϕdϕ																								∫				ρ2d ρ =
					S															0							0
=		2 a2			π∫(cosϕ +3cos2 ϕ +3cos3 ϕ +cos4 ϕ)dϕ =
		3			0
=		2	a	3				+		3				+		1															1		sin	3	ϕ	+
=		3	a		sinϕ			+		2		ϕ		+		2		sin 2ϕ +3 sinϕ −													3		sin		ϕ	+
		3								2						2															3
+		1											1	ϕ +					1							π	=		5			3
		1											1						1							π			5			3
		4	ϕ +sin 2ϕ +																4	sin 4ϕ									4	a π.
		4											2						4							0			4
Отсюда x			=		my	=	5	a .																		0
					my		5

		c			m		6
					m		6

5.3. Найти момент инерции относительно оси Оу площади треугольника с вершинами

А(0, 2a), B (a,0) и С(a, a).

Решение. Покажем треугольник на рис. 1.31.

Рис. 1.31
Уравнение прямой AB :	x	+	y	=1 или	y = 2(a − x);
	a		2a

прямой AC : x−−aa = y a−a или y = 2a − x .

Момент инерции по формуле (4)

Iy = ∫∫x2dxdy = ∫a		x2dx	2a∫−x	dy = ∫a	x3dx = a4 .
S	0		2(a−x)	0	4

5.4.Определить моменты инерции Ix , Iy , I0

прямоугольной пластинки, ограниченной линиями х = 0, х = а, у = 0 и у = b, если плотность ее в каждой точке равна квадрату расстояния точки от начала координат.

Решение. Учитывая, что поверхностная плотность пластинки в точке δ (x, y)= x2 + y2 , по формулам (4) будем

иметь

Ix = ∫∫(x2 + y2 )y2dxdy = ∫a dx∫b (x2 y2 + y4 )dy =

		S							0	0
=	a		2 b3	+	b5		3	a2		+	b2
=	∫0	x	3	+	5	dx = ab			9	+	5	.
	∫0		3		5				9		5

Iy = ∫∫(x2 + y2 )x2dxdy = ∫a dx∫b (x4 + y2 x2 )dy =

			S							0		0
=	a		4	b +	b3	x	2		3	a2		+	b2
=	∫0	x		b +	3	x		dx = a		b	5	+	9	.
	∫0				3						5		9

I0 = ∫∫(x2 + y2 )2 dxdy = ∫a dx∫b (x4 + 2x2 y2 + y4 )dy =

		S									0	0
	a		4		2	2		3		b5		a4			2	2		2		b4
=		x		b +		x	b		+		dx	= ab		+		a	b		+		.
=		x		b +	3	x	b		+	5	dx	= ab	5	+	9	a	b		+	5	.
	∫0				3					5			5		9					5

5.5. Найти полярный момент инерции площади, ограниченной линиями: а) y = 4 − x2 и у = 0; б) ρ2 = a2 cos 2ϕ .

Решение. а) Покажем пластинку на рис. 1.32.

Рис. 1.32

По последней из формул (4) имеем

							2				2						2		4−x2					2				2					2		2					y3		4−x2
							2				2						2		4−x2					2				2					2		2					y3		4−x2
I0 = ∫∫(x								+ y					)dxdy = ∫dx							∫		(x			+ y				)dy = ∫					x			y +						dx =
I0 = ∫∫(x								+ y					)dxdy = ∫dx							∫		(x			+ y				)dy = ∫					x			y +		3				dx =
		S														−2				0													−2						3			0
2		S											1			−2				0			4x3					x5				1	−2					3 16				0
2				2					4				1	(4 − x		2	)	3					4x3					x5				1						3 16				3
=		4x				− x				+									dx		=					−				+			64x −								x		+
=		4x				− x				+			3						dx		=			3		−			5	+		3	64x −						3		x		+
−∫2													3											3					5			3							3
+3	4		x5		−			x7				2		=	4 16		−		64	+		64				4	−4 +				12		−	4		−47,54.
			x5					x7				2			4 16				64			64									12			4


		5						7				−2			3				5				3									5		7
												−2

б) Кривая представляет лемнискату Бернулли (рис. 1.33)

Рис. 1.33

Переходя в последней из формул (4) к полярной системе координат, будем иметь

cos 2ϕ

∫∫(

)

∫∫

+ y2

ρ3d ρdϕ =

∫

dϕ

∫

ρ3d ρ =

dxdy

= a

2ϕdϕ =

πa4

∫cos

sin 4ϕ

5.6. Найти координаты центра тяжести цилиндрического тела, ограниченного поверхностями: х2 + у2 = a2, z = у, z = 0.

Решение. Цилиндрическое тело показано на рис. 1.34. По формулам (5) находим статические моменты

Рис. 1.34

∫a

1 π∫dϕ∫a ρ3 sin2 ϕdϕ =

mxy

∫∫z2dxdy =

dx a

∫−x

y2dy =

−a

2 0

∫(1−cos 2ϕ)dϕ = a π

;

myz

= π∫dϕ∫a

ρ3 sinϕ cosϕd ρ = a4 π∫sinϕd sinϕ = 0.

Масса тела

m = ∫∫zdxdy = π∫dϕ∫a ρ2 sinϕd ρ = a3 π∫sinϕdϕ =

2 a3 .

3 0

Таким образом, по формулам (6) будем иметь

= 0, y

3aπ , z

= 3aπ .

5.7.

Найти

координаты центра

тяжести

момент

инерции

для

части

эллипсоида

=1,

расположенной в первом октанте.

Решение. Рассматривая часть эллипсоида, как

цилиндрическое

тело,

ограниченное

поверхностью

z = c 1−

−

проекция

которой

на

плоскость

Оху

y = b

представляет область: x = 0, y = 0,

a2 − x2

по формулам

(5) находим статические моменты

x2 2

b 1−

−x

cb2

y2 2

mxz = c∫dx

∫

y 1 −

−

dy =−

∫ 1

−

dx =

= cb

∫(a2 − x2 )2 dx

a2bc.

				b	a2 −x2
mxy	=	1	c2	∫a dxa	∫
mxy	=	2	c2	∫a dxa	∫
		2		0	0

		x	2		2		bc	2	a	3			π
1	−			−	y	dy =			∫(a2 − x2 )2		dx =			abc2 .
		a	2		2		3a	3				16
					b				0

По аналогии находим, что myz =

a2bc .

Поскольку тело однородно δ =1 , то масса тела численно

равна объему и находится из решения (4.2.в) V =

π abc .

Таким образом, по формулам (6) имеем

x =

3 a, y

3 b, z

= 3 c .

При вычислении момента инерции

по формуле (8)

воспользуемся интегралами (7)

1−

c b

Ixz = ∫∫y

zdxdy =

∫y

∫

1−

− x

dx =

a 0

= 2πac

−

dy =

πab

∫0

Аналогично

Iyz = ∫∫S x2 zdxdy = 15 πa3bc .

Таким образом

Iz = Ixz + Iyz = 154 πabc (a2 +b2 ).

1.6. Тройной интеграл

1°. Тройной интеграл является обобщением понятия двойного интеграла на случай функции трех переменных f(x,y,z) и представляет конечный предел трехмерной интегральной суммы в области V

∫∫∫ f (x, y, z)dxdydz = maxlimx →0 ∑∑∑ f (xi , yj , zk )				xi y j zk , (1)
(V )		i	i j k
(V )	max	y j →0	i j k
	max	zk →0
где xi yj zk = (xi+1 − xi )(y j+1 − y j )(zk +1 − zk ) -				объем элемен-

тарных областей, на которые разбивается пространственная область V.

Для непрерывной в области V функции f(x,y,z) предел (1) существует и не зависит от способа разбиения области Кна элементарные области объемом xi y j zk , от выбора точки в

каждом элементарном объеме, в которой вычисляется f(x,y,z), и от способа стремления наибольшего диаметра элементарной области к нулю.

Основные свойства тройных интегралов аналогичны свойствам двойных интегралов.

2°. Вычисление тройного интеграла сводится к последовательному вычислению трех обыкновенных определенных интегралов

	x		y (x)		z	(x, y)
∫∫∫ f (x, y, z)dxdydz = ∫2		dx	2∫	dy	2	∫ f (x, y, z)dz .	(2)
V	x1		y1 (x)		z1 (x, y)

Если внутренний интеграл берется по переменной z, то переменные (х, у) при интегрировании его рассматриваются как постоянные величины. Пределы интегрирования во внутреннем интеграле, как правило, являются переменными и зависят от (х, у). Таким образом, задача сводится к вычислению двойного интеграла, у которого пределы интегрирования внутреннего интеграла в общем случае зависят от переменной х, а пределы интегрирования внешнего интеграла постоянны.

3°. Пусть в тройном интеграле требуется от переменных х, у, z перейти к переменным u, v, w, связанным соотношениями

x = x (u, v, w), y = y (u, v, w), z = z (u, v, w).

(3)

Функции (3) осуществляют взаимно-однозначное и непрерывно дифференцируемое отображение области G

пространства Ouvw на область V пространства Oxyz. Если якобиан этого отображения

	∂x	∂x	∂x
	∂x	∂x	∂x
	∂u	∂v	∂w
I =	∂y	∂y	∂y	≠ 0
I =	∂u	∂v	∂w	≠ 0
	∂u	∂v	∂w
	∂z	∂z	∂z
	∂u	∂v	∂w

не обращается в нуль на G и функция f(x,y,z) непрерывна в области V, то справедлива формула

∫∫∫ f (x, y, z)dxdydz =

V			(4)
= ∫∫∫ f (x (u, v, w), y (u, v, w), z (u, v, w))	I	dudvdw.


G

Производить замену переменных по формулам (3) следует в том случае, если область интегрирования G в интеграле (4) значительно проще области V.

Если при вычислении тройного интеграла целесообразнее перейти от переменных х, у, z к цилиндрическим координатам ρ,ϕ, z (рис. 1.35), связанным с

декартовыми координатами соотношениями x = ρ cosϕ, y = ρsinϕ, z = z

(0 ≤ ρ < +∞, 0 ≤ϕ ≤ 2π, −∞ < z < +∞),

то формула преобразования имеет вид

∫∫∫ f (x, y, z)dxdydz = ∫∫∫ f (ρ cosϕ, ρsinϕ, z)ρd ρdϕdz . (5)

V G

Рис. 1.35

В случае перехода от декартовых координат х, у, z к сферическим координатам ρ,ϕ,θ (рис. 1.36), связанным с x,y,z

соотношениями x = ρsinθ cosϕ, y = ρ sinθ sinϕ, z = ρ cosθ

(0 ≤ ρ < +∞, 0 ≤ϕ ≤ 2π, 0 ≤θ ≤π ),			где якобиан преобразо-
вания равен
I =	sinθ cosϕ	−ρsinθ sinϕ	ρ cosθ cosϕ	= ρ2 sinθ ,
	sinθ cosϕ	−ρsinθ sinϕ	ρ cosθ cosϕ
	sinθ sinϕ	ρ sinθ sinϕ	ρ cosθ sinϕ
	cosθ	0	−ρ sinθ
формула преобразования тройного интеграла имеет вид
∫∫∫ f (x, y, z)dxdydz =
V					(6)
= ∫∫∫ f (ρ sinθ cosϕ, ρ sinθ sinϕ, ρ cosθ )ρ2 sinθdpdϕdθ.					(6)

Рис. 1.36

							1	x	y
	6.1. Вычислить следующие интегралы: а) ∫dx∫dy∫xyzdz ;
							0	0	0
б) ∫2 dx 2 x∫−x		2	z x2 + y2 dz ; в) ∫1	dx 1∫−x	2	1−x2 −y2
б) ∫2 dx 2 x∫−x		dy∫a	z x2 + y2 dz ; в) ∫1	dx 1∫−x		dy ∫	x2 + y2 + z2 dz .
0	0	0	0	0		0

Решение. а) Вычисление тройного интеграла начинается с вычисления внутреннего интеграла. Полагая х и у постоянными, интегрируем по z, тогда получим

I = ∫1 dx∫x xy		z2	y dy =	1	∫1	dx∫x xy3dy .

		2		2
0	0		0		0	0

Таким образом, тройной интеграл свелся к двойному. Вычисляем теперь двойной интеграл

I =	1	∫1	x	y4	xdx =	1	∫1 x5dx =	1	.

	2					8		48
		0	4		0		0

б) Данный интеграл следует вычислять в цилиндрической системе координат. Однако, целесообразнее сначала найти внутренний интеграл по z, а затем перейти к полярной системе координат

I = ∫2 dx	2 x∫−x2		z2	a	dy = a2	∫2 dx 2 x∫−x2
		x2 + y2						x2 + y2 dy .

0	0	2		0	2	0	0

Область интегрирования последнего интеграла показана на рис. 1.37. Переходя к полярным координатам x = ρ cosϕ ,

y = ρsinϕ , будем иметь

		π		2cosϕ							π									π
	a2 2			2cosϕ						8a2 2							4			2			)
	a2 2			∫		2				8a2 2			3				4		2	2		2
I =		∫	dϕ	∫	ρ		d ρ =				∫	cos		ϕdϕ =				a		∫(	−sin
I =	2		dϕ		ρ		d ρ =			6		cos		ϕdϕ =			3	a		1	−sin		ϕ d sinϕ =
	2	0		0						6	0						3			0
					4						1				π		8
				=	4	a		2			1	sin	3		2	=	8		2	.
				=	3	a			sinϕ −		3	sin		ϕ		=	9	a		.
															0
															0

<<< < Предыдущая 1 2 3 45 / 225 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20221.79 Mб9Учебное пособие 1694.pdf
#
30.04.20221.79 Mб25Учебное пособие 1695.pdf
#
30.04.20221.8 Mб6Учебное пособие 1696.pdf
#
30.04.20221.8 Mб2Учебное пособие 1697.pdf
#
30.04.20221.8 Mб2Учебное пособие 1698.pdf
#
30.04.20221.81 Mб7Учебное пособие 1699.pdf
#
30.04.2022207.49 Кб6Учебное пособие 17.pdf
#
30.04.2022310.52 Кб19Учебное пособие 170.pdf
#
30.04.20221.81 Mб4Учебное пособие 1700.pdf
#
30.04.20221.81 Mб9Учебное пособие 1701.pdf
#
30.04.20221.81 Mб5Учебное пособие 1702.pdf