
Учебное пособие 1692
.pdf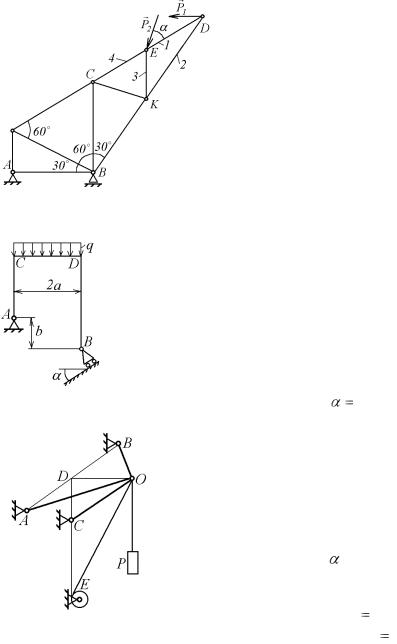
ние реакции ZA противоположно направлению, указанному на рис. 8.20.
§ 8.6. Задачи для само-
|
|
стоятельного решения |
|
||
|
|
8.1. Груз |
массой |
m = |
|
|
|
6000 кг подвешен при помо- |
|||
Рис. 8.22 |
щи каната, перекинутого че- |
||||
|
|
рез небольшой блок А и иду- |
|||
щего к лебедке D. Определить силы в стержнях АС и ВА крана. |
|||||
|
Углы, определяющие положения осей стерж- |
||||
|
ней показаны на рис. 8.21. |
|
|
|
|
|
|
8.2. Плоская ферма (рис. 8.22.), состоя- |
|||
|
щая из невесомых стержней, соединенных |
||||
|
между собой по концам шарнирами, находит- |
||||
|
|
|
|
|
|
|
ся в равновесии под действием сил P |
и P , |
|||
|
|
|
1 |
2 |
|
|
причем сила P1 горизонтальна, сила P2 со- |
||||
Рис. 8.23 |
ставляет со стержнем ED угол |
45 . Оп- |
|||
|
ределить силы в стержнях 1, 2, 3 и 4 если |
||||
|
|
P1 =30 кН, P2 = 20 кН. |
|
|
|
|
|
8.3. Жесткая рама (рис. 8.23) за- |
|||
|
|
креплена в точке А при помощи под- |
|||
|
|
вижного цилиндрического шарнира, а в |
|||
|
|
точке В опирается катками на гладкую |
|||
|
|
наклонную поверхность, составляю- |
|||
|
|
щий с горизонтом угол |
= 30 . На го- |
||
|
|
ризонтальном участке CD рама нагру- |
|||
|
|
жена равномерно распределенной на- |
|||
Рис. 8.24 |
|
грузкой интенсивностью |
q |
5 |
кН/м. |
Определить реакции опор в точках А и В, если CD= 2a |
1,2 м, |
||||
|
|
176 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ОК= b ( |
|
3 1)a . |
|
|
||||
|
|
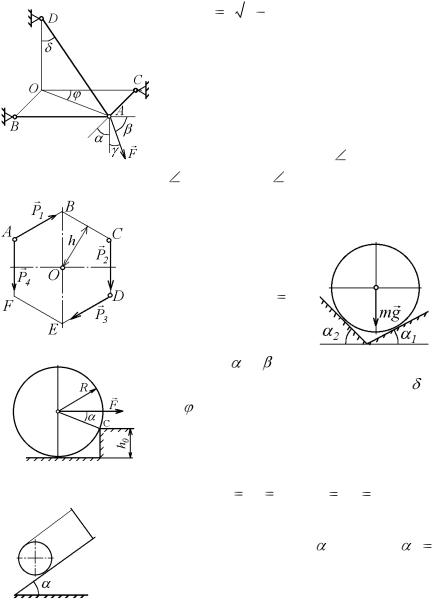
8.4. Груз |
массой |
m = 1000 |
кг |
||||
|
поддерживается при помощи каната, |
||||||||
|
перекинутого через блок О и идущего |
||||||||
|
к лебедке Е (рис. 8.24.). Определить |
||||||||
|
силы в стержнях АО, ОВ, ОС крана, |
||||||||
|
если поверхность ОАВ горизонтальна, |
||||||||
Рис. 8.25 |
AD= DB, ОА= ОВ, |
DCO= 60 , |
|||||||
|
СОЕ= 30 и |
АОВ= 90 . |
|
||||||
|
|
|
|||||||
|
8.5. Невесомые стержни АС, АВ и AD |
||||||||
|
соединены шарнирно между собой в точке |
||||||||
|
А и |
с неподвижными |
|
|
|||||
|
опорами в точках С, D и |
|
|
||||||
|
В (рис. 8.25.). К узлу А |
|
|
||||||
|
приложена сила F |
8 |
|
|
|||||
Рис. 8.26 |
кН, |
составляющая с |
Рис. 8.27 |
|
|||||
|
координатными осями |
|
|||||||
|
|
|
|||||||
|
х и у углы |
= |
= 60 . Определить ре- |
||||||
|
акции стержней АС, АВ, и AD, если |
= |
|||||||
|
60 , |
= 45 . |
|
|
|
|
|
|
|
Рис. 8.28 |
|
8.6. Найти равнодействующую че- |
|||||||
тырех сил, |
действующих по сторонам |
||||||||
|
|||||||||
правильного шестиугольника, направление которых указано на
|
рис. 8.26, если P1 |
P3 2P , P2 |
P4 |
P . |
|
|
8.7. Две наклонные поверхности, обра- |
||||
Рис. 8.29 |
зующие с горизонтом углы |
1 = 25 |
и |
2 |
|
45 (рис. 8.27.), |
сдвинуты так, что образуют |
||||
двугранный угол. На этих поверхностях лежит шар массой m = 2 кг. С какой силой давит шар
на эти поверхности?
177
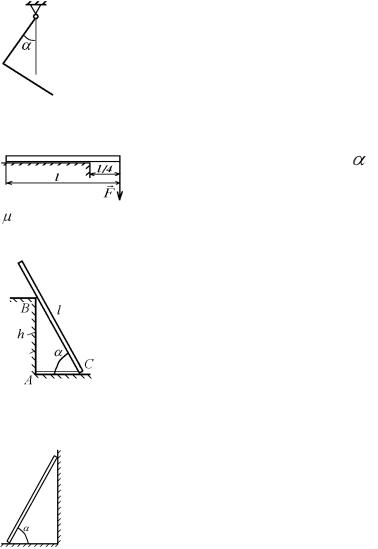
8.8. Тяжелый цилиндрический каток массой m необходимо поднять на ступеньку высотой h . Найти
минимальную силу F , которую нужно приложить к центру масс катка в горизонтальном направлении,
если радиус катка R больше высоты h (рис.
8.28).
8.9. На цилиндр намотана нить, один конец которой креплен на стержне в верхней точке наклонной плоскости. При
каком угле наклона плоскости цилиндр не будет скатываться с нее, если коэффициент трения цилиндра о плоскость равен
.
8.10. Тяжелый стержень (рис. 8.30) согнут по середине под прямым углом и подвешен свободно за один из концов. Какой угол с вертикалью разует верхняя половина стержня?
8.11. Однородная балка лежит на плат-
Рис. 8.32 форме так, что ее один конец свешивается с платформы (рис. 8.31). Длина свешивающегося
конца балки равна четверти длины балки. К
свешивающемуся концу балки прикладывают силу F , ленную вертикально в низ и равную 2000 Н. При этом противоположный конец балки начинает подниматься.
Чему равен вес балки?
8.12. Однородная балка массой m, такой, что mg 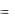 1200 Н, и длиной l
1200 Н, и длиной l 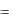 2 м опирается на гладкий пол и гладкий выступ В, расположенный на высоте h
2 м опирается на гладкий пол и гладкий выступ В, расположенный на высоте h 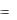 1,5 м над полом (рис. 8.32). Балка состав-
1,5 м над полом (рис. 8.32). Балка состав-
ляет с вертикалью угол и удерживается веревкой Рис. 8.33 АС, натянутой у пола. Найти силу натяжения ве-
ревки и реакции пола и выступа.
178
8.13. Лестница длиной l = 2 м, центр тяжести которой находится в ее середине, приложена к стене и находится в равновесии (рис. 8.33). Угол, образованный лестницей с горизонта-
лью равен 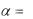 53 . Найти силы действующие на лестницу со стороны стены и земли, если сила тяжести, действующая на лестницу равна P
53 . Найти силы действующие на лестницу со стороны стены и земли, если сила тяжести, действующая на лестницу равна P 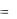 80 Н, а трение между лестницей и стеной отсутствует.
80 Н, а трение между лестницей и стеной отсутствует.
8.14. Однородная балка АВ =
l массой m 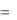 600 кг, закреплена в точке А шарнирно, наклонена к горизонтали
600 кг, закреплена в точке А шарнирно, наклонена к горизонтали
под углом = 30 (рис. 8.34). Балка удерживается в равновесии при помо-
щи прикрепленной к ней в точке В веревке ВDЕ, перекинутой через неподвижный блок D, к свободному концу которой подвешен груз Е весом P . Балка находится под действием перпендикулярной к ней равномерно распределенной нагрузки интенсивностью q = 2 кН/м и вертикальной силы F = 1 кН,
приложенной в точке С, такой что AC / CB |
1/ 3 . Веревка BD |
|
составляет с вертикалью угол |
||
= 30 . Определить вес груза P , |
||
если АВ= 3м. |
|
|
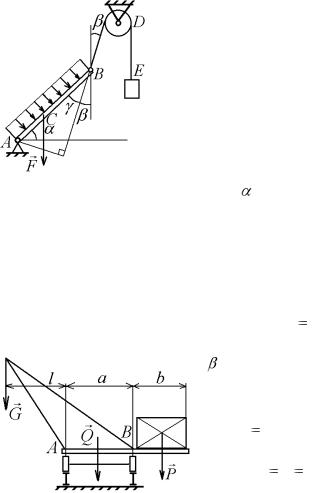
8.15. Подъемный кран ве- |
||
сом Q |
20 кН имеет вылет |
|
стрелы l = 5 м и ширину основа- |
||
ния AB |
a |
4 м. Вес противо- |
веса, имеющего форму куба с ребром b 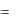 2 м, равен P
2 м, равен P 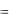 5 кН и приложен в центре куба. Сила тяжести крана приложена в точке, находящейся на пря-
5 кН и приложен в центре куба. Сила тяжести крана приложена в точке, находящейся на пря-
мой, проходящей через середину отрезка АВ. Найти наиболь-
ший вес груза G , который может поднять кран без опрокидывания вокруг точки А (рис. 8.35).
179
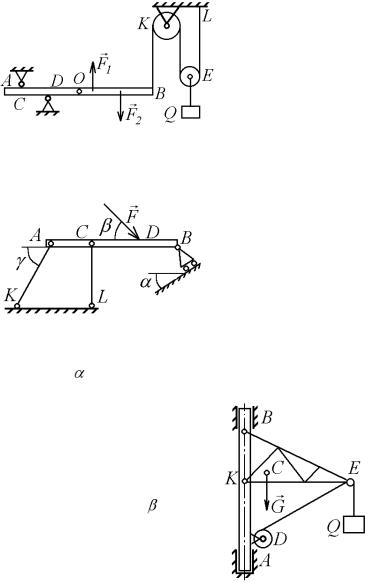
8.16. Однородная горизонтальная балка АВ= 1,5 м и весом P = 1500 Н, заложенная между двумя опорами С и D, находится под действи-
|
|
|
ем пары сил ( F1 |
и |
F2 ) с мо- |
ментом m = 100Н*м (рис. Рис. 8.36 8.36). К конце балки В при-
креплена веревка, переброшенная через блоки К и Е, другой конец которой закреплен неподвижно в точке L. К центру под-
вижного блока Е подвешен груз весом Q = 400 Н. Опреде-
|
лить реакции опор С и D, если |
|
АС= 25 см. Трение в блоках не |
|
учитывать. |
Рис. 8.37 |
8.17. Однородная гори- |
|
|
|
зонтальная балка (рис. 8.37) |
АВ= 1,5 м весом P = 120 Н концом В опирается при помощи катков на гладкую поверхность, наклоненную к горизонтали
под углом = 30 , а в точках А и С балка соединена шарнирно с невесомым стержнями АК и СL, шарнирно закрепленными в
неподвиж- ных точках
К и L.
В точке D под углом = 45 |
к |
Рис. 8.38 |
|
|
балке приложена сила F = 60
Н. Определить
реакции опор А, С и В, если АD= 5 DB, ВС= 2 СА, стержень CL вертикален, а стержень АК составляет с осью балки угол 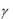 =
=
60 .
180
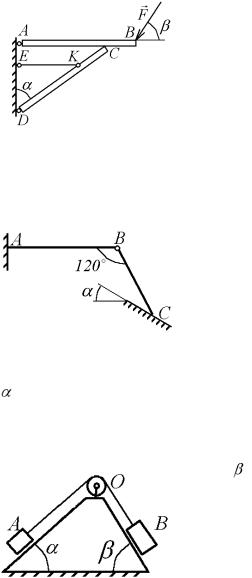
8.18. Вертикальная ось АВ подъемного крана (рис.8.38), вес которого равен G = 15 кН, может вращаться в подпятнике А и подшипнике В. Груз весом Q = 8,4 кН
поднимается при помощи веревки, перекинутой через блок Е и идущий к лебедке D, закрепленной на оси
крана (рис. 8.). Определить реакции подшипника и подпятника, если
центр тяжести С отстоит от оси вращения на расстояние, рав-
ное 0,9 м, АВ= 12 м, КЕ= 4 м.
|
8.19. Однородная горизон- |
|
тальная балка (рис. 8.39) АВ длиной |
|
6 м и весом P1 = 2400 Н, закреплен- |
|
ная в неподвижной точке А шар- |
|
нирно, свободно опирается в точке |
|
С на подпорную балку СВ длиной 5 |
Рис. 8.40 |
м и весом P2 = 3200 Н. Балка CD , |
|
составляющая с вертикалью угол |
= 60 , закреплена в точке D при помощи неподвижного цилиндрического шарнира и удерживается в равновесии при помощи горизонтальной веревки ЕК, причем DE= 2 м. В точке В к балке приложена сила F =1200 Н, наклоненная к балке под
углом = 60 . Определить реакции шарниров А и D, силу натяжения веревки T и силу RC давления балки АВ на балку CD, если точки А и
Dлежат на одной вертикали.
8.20.Две однородные балки
Рис. 8.41 АВ= 4 м и весом P1 = 60 Н и ВС= 3 м и весом P2 = 40 Н соединены в
точке В шарнирно. Первая балка горизонтальна и концом А
181
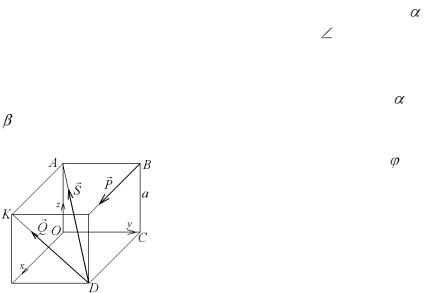
заделана жестко, а вторая концом С свободно опирается на |
|
|
гладкую поверхность, наклоненную к горизонту под углом |
= |
|
30 . Определить реакции в точках А и С, если |
АВС= 120 |
|
(рис. 8.40). |
|
|
8.21. Два груза А и В (рис. 8.41), массы которых равны |
|
|
m1 и m2 , лежащие на наклонных поверхностях с углами |
и |
|
, связаны веревкой, перекинутой через блок О. Найти соотношение масс грузов при равновесии системы, если углы тре-
ния грузов о поверхности равен .
8.22. К вершинам C, B и D куба со стороной a приложены равные по
модулю силы P , S и Q , направлен-
ные соответственно по стороне ВЕ и по диагоналям DA и DK. Найти моменты каждой из из этих сил относи-
тельно координатных осей х, у, z (рис.
Рис. 8.42 8.42).
182
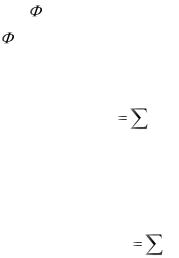
Глава 9. УСЛОВИЯ ЭКВИВАЛЕНТНОСТИ СИСТЕМ СИЛ
§9.1. Условие эквивалентности систем сил
Внастоящей главе рассмотрены некоторые свойства систем сил и теоремы, которые позволяют существенно упростить исследование систем сил и решение задач.
Совокупность нескольких сил называют системой сил. Для сокращения записи систему сил, состоящую из n
~
сил P1 , P2 , ,Pn , будем обозначать символом Pn .
Если на тело одновременно действуют две системы сил, |
||||
|
~ |
|
~ |
|
например Pn |
и |
m , то полная система сил обозначается сим- |
||
~ |
~ |
m ). |
|
|
волом ( Pn , |
|
|
||
|
|
|
~ |
|
Главным вектором произвольной системы сил Pn |
назы- |
|||
вается вектор, равный векторной сумме всех сил системы
V |
Pk . |
(9.1) |
~
Главным вектором моментом произвольной системы сил
Pn относительно некоторой точки О называется вектор, рав-
ный векторной сумме моментов всех сил системы относительно этой точки
|
|
|
|
MO |
MO ( Pk ) . |
(9.2) |
|
Две системы сил называют эквивалентными, если они, будучи приложенными поочередно, каждая в отдельности к одному и тому же абсолютно твердому телу окажут одинаковое действие на тело.
183

Теорема 9.1. Для эквивалентности двух систем сил необходимо и достаточно, чтобы были равны их главные векторы и главные моменты относительно произвольной точки
Доказательство необходимости. Дано:
|
|
|
|
|
|
( P1 ,P2 , ,Pn ) |
( Ф1 ,Ф2 , ,Фm ) |
(9.3) |
|||
|
|
~ |
|
~ |
|
или в сокращенной записи: |
Pn |
|
Фm . Надо доказать, равенст- |
||
во главных векторов и главных моментов этих систем сил.
|
|
|
|
|
|
|
|
Рассмотрим систему сил - P1 , |
- P2 , …, |
Pn где сила |
Pk |
|
|||
приложена в той же точке, что и |
|
(k = 1, 2, ..., n). Главные |
|||||
Pk |
|||||||
|
|
|
|
|
|
|
|
векторы систем сил P и - |
P обозначим символами VP |
и V |
P |
, |
|||
|
|
|
|
|
|
|
|
а главные моменты- M0( P ) |
и M0( |
P ) |
. Тогда |
|
|
|
|
|
|
|
V P |
P1 |
P2 |
M0( P )
( rk
Отсюда
|
|
|
Pn |
( P1 |
P2 |
|
|
|
M0 ( |
Pk ) |
[ rk |
|
|
|
Pk ) |
M0 ( Pk ) |
|
|
|
Pn ) |
VP , |
( Pk )]
M0( P ) .
|
|
|
|
|
|
|
V P |
VP |
0, M0( P ) |
M0( P ) |
0 , |
(9.4) |
|
|
|
|
|
|
|
|
т. е. главный вектор и главный момент системы сил ( P , - |
P ) |
|||||
равны нулю. Следовательно, в соответствии с теоремой о рав-
новесии произвольной системы сил рассматриваемая система |
|||||
|
|
|
|
|
~ |
является уравновешенной. Согласно условию (9.3) систему Pn |
|||||
заменим эквивалентной системой |
~m . Тогда снова получаем |
||||
|
|
|
|
|
|
уравновешенную систему сил |
( Ф1 ,Ф2 , ,Фm , |
P1 , |
P2 , |
||
|
|
|
|
|
|
..., Pn ) 0 . По теореме о равновесии сил, |
главный вектор и |
||||
главный момент последней системы должны быть равны нулю. Тогда, используя (9.4), получаем
184

|
|
|
|
|
|
|
|
|
|
M0( P ) |
M0( ) |
M0( P ) |
M0( ) |
M0( P ) |
0 , |
||
|
|
|
|
|
|
|
|
|
|
VФ, P |
|
VФ |
V P |
VФ |
VP |
0 . |
|
|
Отсюда следует то, что и требовалось доказать: VФ |
VP , |
||||||
|
|
|
|
|
|
|
|
|
M0( |
) M0( P ) . |
|
|
|
|
|
|
|
|
Доказательство достаточности. Даны главные векторы и |
|||||||
главные моменты двух систем сил |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
VФ |
VP , |
M 0( Ф ) |
M 0( P ) |
(9.5) |
|||
Надо доказать, что системы сил эквивалентны. Учитывая
(9.4) и (9.5), получим, что главный вектор и главный момент |
||||||||
|
|
|
|
|
|
|
|
|
системы ( P1 , |
P2 , , Pn ,Ф1 |
,Ф2 , ,Фm ) |
равны нулю, т. е. эта |
|||||
система сил находится в равновесии. Тогда |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
V |
P,Ф |
V |
P VФ |
VP |
VФ |
0 , |
|
|
|
|
|
|
|
|
|
|
M0( P,Ф ) |
M0( P ) |
M0( Ф ) |
M0( P ) |
M0( Ф ) |
0 . |
|||
Согласно третьей аксиоме, уравновешенную систему сил
можно присоединять и исключать, не изменяя действие других |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
сил на тело. Присоединим к системе Pn |
уравновешенную сис- |
|||||||||||||
~ |
|
~ |
m ) |
|
|
|
|
|
|
|
|
|
|
|
тему сил (- Pn , |
|
|
0, а затем исключим уравновешенную |
|||||||||||
~ |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
систему (- Pn , Pn ) |
|
0: |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( P1 |
,P2 |
, ,Pn ) |
( P1 |
,P2 |
, ,Pn , P1 |
, P2 , |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
..., |
|
Pn ,Ф1 |
,Ф2 |
, ,Фm ) |
(Ф1 ,Ф2 |
, ,Фm ) . |
|||||||
|
|
|
|
|
~ |
|
~ |
|
|
|
|
|
|
|
Итак, системы Pn |
и |
|
m |
эквивалентны, что и требовалось |
||||||||||
доказать.
Примечание. Если система сил плоская, то главные момент системы относительно данного центра, расположенного в
185
