Учебное пособие 1692

но пропорциональные модулям этих сил. Две неравные по модулю и противоположно направленные параллельные силы имеют равнодействующую, параллельную этим силам, направленную в сторону большей силы, равную по модулю абсолютному значению алгебраической суммы модулей слагаемых сил и делящей внешним образом отрезок между точками приложения данных сил на части, обратно пропорциональные модулям этих сил.

Центром параллельных сил, приложенных к твердому телу, называют точку, через которую проходит линия действия равнодействующей параллельных сил при любом их направлении в пространстве, если величины и точки приложения сил остаются постоян-

Рис. 10.2 ными. Пусть в точках A1 (x1, y1, z1); A2 (х2, у2, z2); A3(x3, y 3, z 3)

приложены параллельные силы P1 , P2 , P3 (рис. 10.2), а в точ-

В аналитической геометрии рассматривается формула для координаты точки, делящей отрезок в заданном отношении, определяемом величиной

действующую R1,2,3=R1,2+ P3 = P1 + P2 + P3, приложенную в точке C2(xC2, yC2, zC2). Для трех сил

196

Координаты yC и zC определяются аналогично.

В сокращенной записи эти формулы имеют вид

Если поворачивать силы вокруг своих точек приложения, оставляя их параллельными и сохраняя их модули, то ничто в приведенном выводе и полученных выражениях не изменится. Таким образом, формулы (10.2) определяют центр параллельных сил.

которые, учитывая большой радиус Земли, можно считать параллельными с большой точностью. Центром тяжести системы материальных точек называют центр параллельных сил, являющихся силами тяжести всех точек системы. Таким образом, формулы (10.2) одновременно определяют центр тяжести тела или системы.

Оси координат, проходящие через центр тяжести тела или системы тел называются центральными осями тела или

197

системы тел. Соответствующая система координат называется центральной системой координат.

Следует отличать центр масс тела от его центра тяжести. Для тел малых размеров эти центры совпадают. Для больших по размерам систем тел ускорения силы тяжести в окрестностях разных тел системы различны и центр тяжести системы не совпадает с ее центром масс.

10.1.3. Центры тяжести однородных тел Если материальные точки расположены не изолированно

(дискретно), а распределение массы сплошное, например как в твердом теле, то для определения центра тяжести такое тело

g V2, ... , Gn = g 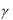Vn, где - плотность материала тела; g - ускорение свободного падения.

Преобразуем формулы (10.2)

Для определения центра тяжести плоского тела, вместо элементов объема в (10.3) используются элементы площади и соответствующие формулы принимают вид

198

Для определения центров тяжести тел, у которых поперечные размеры значительно меньше продольного размера (длины) и постоянны, например, для стержней или проволоки, в формулах (10.3) вместо элементов объема используют элементы длины lk.

Величина , характеризующая материал тела, в формулы (10.3), (10.4) не входит. Координаты центра масс однородного тела зависят от формы и размеров тела, но не зависят от характеристик материала тела. Это значит, что если один и тот же объем (или плоскую фигуру) заполнить поочередно однородным материалом - медью, железом, цинком и т. д., то положение центра тяжести не изменится.

Для того чтобы суммы в числителях и знаменателях формул (10.3) и (10.4) не зависели от числа слагаемых и от форм элементов, на которые разбивается тело, тело нужно разбить на бесконечно большое количество бесконечно малых элементов объема или площади, т. е. получить определенные интегралы по объемной или плоской области, занимаемой телом.

При приближенном определении координат центра тяжести тела или системы тел, а также некоторых тел простых форм, можно разбивать тела на конечное число элементов, и тогда получаются суммы с конечным числом слагаемых. Если плоская фигура расположена в плоскости (ху), то координата хk будет расстоянием от элемента площади Fk до оси у, a yk - расстоянием от этого элемента до оси х.

10.1.4. Статические моменты плоских фигур Статическим моментом плоской фигуры относительно

данной оси называют сумму произведений всех элементарных площадей фигуры на расстояния от их центров тяжести до данной оси.

Статические моменты Sy и Sz фигуры относительно осей х и у определяются по формулам

199

В формулах (10.5) интегралы по способу вычисления являются двойными интегралами по плоской области, занятой телом.

Если плоская фигура расположена в плоскости ху, то все zk = 0, и тогда (10.4) можно записать в виде

Ось, проходящая через центр тяжести фигуры, называется центральной осью фигуры.

Система координат, оси которой являются центральными осями фигуры, называется центральной системой координат.

При решении задач по определению центров тяжести используются методы группировки, симметрии и отрицательных масс.

Первый метод применяют в тех случаях, когда можно так сгруппировать элементы тела, что центры тяжести и размеры выделенных элементов или известны, или их легко определить. Далее используют формулы (10.3), (10.4).

Метод симметрии основан на следующей теореме (примем без доказательства): если однородное тело имеет плоскость, ось или центр симметрии, то центр тяжести такого тела находится соответственно в плоскости, на оси или в центре симметрии.

Метод отрицательных масс заключается в том, что если в теле имеется отверстие, то площадь и статический момент отверстия во всех вычислениях считают отрицательными.

200

Пример 10.1. Определить координаты центра тяжести пластины, изображенной на рис. 10.3; размеры даны в см.

Решение. Разбиваем пластину на четыре фигуры: два прямоугольника 1 и 2, треугольник 3 и круг 4, причем площадь круга, как площадь отверстия, считаем отрицательной, а площадь прямоугольника 2 вычисляем, считая, что отверстие отсутствует:

F1 = 20 30 = 600 см2, F2 = 30 30 = 900 см2, F3 = 0,5 30 30 = 450 см2, F4 = - r2 = -314 см2.

Рис. 10.3

Выбираем систему координат с таким расположением осей координат, чтобы было удобно определять координаты центров тяжести составных элементов фигуры. Определяем координаты центров тяжести всех элементов фигуры. Центр тяжести треугольника находится в точке пересечения его медиан, т. е. на расстоянии одной трети длины каждой медианы от соответствующей стороны треугольника. Тогда

х1 = -15 см; y1 = 10 см; х3 = 20 см; у3 = 40 см; х2 = 15 см; у2 = 15 см; х1 = 15 см; y1 = 15 см.

201

По формулам (10.5) и (10.6) находим координаты центра тяжести пластины

Пример 10.2. Определить положение центра тяжести симметричного сечения, показанного на рис. 10.4, состоящего из полосы размером 120 х 10 мм, двутавра № 12 (ГОСТ 823972) и швеллера № 14 (ГОСТ 8240-72).

Решение. Разбиваем сечение на три фигуры: 1 - полоса, 2 - двутавр и 3 - швеллер. Находим площади каждой части, выражая их в см2. При этом площади двутавра и швеллера берем из таблиц ГОСТа: F1 = 12 1 = 12 см2; F2 = 14,7 см2; F3 = 15,6 см2.

Выбираем оси координат так, чтобы ось y совпала с осью симметрии, а ось х прошла через центр тя-

жести двутавра. Определяем рас- Рис. 10.4 стояния от центров фигур до оси х2,

проходящей через центр тяжести двутавра: у1 = - (h/2 + 0,5) = - (12/2 + 0,5) = - 6.5 см (где h - высота двутавра); у2 = 0; у3 = h/2

202

+ х0 = 12/2 + 1.67 = 7.67 см (где х0 - координата центра C3 масс швеллера, определяемая по таблице ГОСТа).

По (10.4) находим координаты центра масс всего сечения

§ 10.2. Геометрические характеристики поперечных сечений стержня

При решении различных задач по со-

F dF .

F

Статические моменты сечения, как было указано в предыдущем параграфе, определяются выражениями

Осевые моменты инерции сечения относительно осей х1

и y1

Здесь dF – элемент площади сечения, а F – площадь сечения.

203

Осевые моменты инерции всегда положительны и не могут быть равны нулю.

Они измеряются в единицах длины в четвертой степени, например, в см4.

10.2.1. Зависимость между моментами инерции относительно параллельных осей

Пусть точка С является цен-

Первый интеграл равен моменту инерции J, относительно оси х, второй интеграл обращается в нуль, поскольку ось х проходит через центр тяжести (см. (10.6)), а третий интеграл есть площадь сечения. Следовательно,

т. е. момент инерции сечения относительно произвольной оси, лежащей в его плоскости, равен моменту инерции относительно центральной оси, параллельной этой оси, плюс произведение площади сечения на квадрат расстояния между осями.

Соотношения (10.8) выражают теорему Штейнера. Радиусы инерции сечения относительно осей х и у

Радиусы инерции измеряются в единицах длины, например в см.

204

10.2.2. Полярный момент инерции Полярный момент инерции есть момент инерции сечения

относительно оси, перпендикулярной плоскости сечения. Его определяют выражением

F

где каждый элемент площадью dF умножается на квадрат расстояния до точки О пересечения оси с плоскостью сечения.

Следовательно, полярный момент инерции относительно произвольной точки О равен сумме моментов инерции относительно взаимно перпендикулярных осей, проходящих через ту же точку.

При повороте осей вокруг точки, являющейся началом системы координат, сумма осевых моментов инерции остается неизменной, т. е.

Это выражение удобно использовать для вычисления неизвестного осевого момента инерции по известным полярному и осевому моментам инерции.

10.2.3. Центробежный момент инерции Центробежный момент инерции сечения относительно

осей х1 и y1 (см. рис. 10.5) определяется как интеграл:

J x1 y1 x1 y1dF , (10.13)

F

205