
Учебное пособие 1431
.pdfL |
10y2 x 10 |
|
0 |
||||||||||||
|
|
|
|||||||||||||
|
|
||||||||||||||
x |
|
L |
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
20xy |
0 |
|
||||||||||
|
|
|
|
|
|
||||||||||
|
y |
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
L |
|
x |
|
|
y |
1 0 |
|
||||||
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
7 2 |
|
|
|
|
|
|||||||
Первое уравнение умножим на 7, второе на 2 и сложим |
|||||||||||||||
их. Этим исключим параметр из системы: |
|
||||||||||||||
70y2 40xy 14x 70 0 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
7y |
7 |
|
|
|
||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|||||
Непосредственной подстановкой приходим к уравнению,
которое после сокращений имеет вид 30y2 47y 4 0. Отсю-
да находим y1 1,5, y2 0,1 |
и из системы получаем точки |
|
M1 1,75;1,5 ,M2 6,65;0,1 , |
принадлежащие отрезку AB |
|
.Вычисляем значения функции в стационарных точках |
||
z M1 z 1,75;1,5 25,9, |
||
z M2 z 6,65;0,1 22,9 |
||
и на концах отрезка |
|
|
z A z 7;0 20, |
z B z 0;2 1. |
|
Сравнивая все полученные величины, приходим к выводу: наибольшее значение функции на отрезке достигается в точке A, а наименьшее в точке M1.
Пример 2.Найти наибольшее и наименьшее значения функции z 2x3 6xy 3y2 в замкнутой области, ограниченной осью
Oy , прямой y 2 и параболой y x2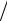 2 при x 0 (рис. 13).
2 при x 0 (рис. 13).
71

y |
|
|
|
2 A |
Q |
|
B |
1 |
H |
|
|
|
P |
|
|
O |
|
|
x |
0 |
1 2 |
2 |
Рис. 13
Решение.
1) Находим стационарные точки функции.
|
z |
6x2 6y; |
z |
6x 6y . |
|||
|
|
|
|||||
|
x |
|
|
|
y |
||
|
|
|
6x |
2 |
6y 0 |
||
|
|
|
|
||||
Решив систему уравнений |
|
|
|
, |
|
||
6x 6y 0
получим две стационарные точки O 0,0 и H 1,1 . Первая из них принадлежит границе области. Следовательно, если функция z принимает наибольшее (наименьшее) значение во внутренней точке области, то это может быть только в точке H 1,1 .
Найдем z(H) z(1;1) 1.
2) Исследуем функцию на границе области
а) на отрезке OA имеем x 0, поэтому z 3y2 0 y 2 - возрастающая функция одной переменой y ; наибольшее и наименьшее значения она принимает на концах отрезка OA.
Найдем z O z 0;0 0; |
z A z 0;2 12; |
б) на отрезке AB имеем y 2 , следовательно,
z 2x3 12x 12 0 x 2 представляет функцию одной переменной x; ее наибольшее и наименьшее значения находятся среди ее значений в критических точках и на концах отрезка. Решая уравнение z 6x2 12 0, находим x1,2 
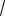 2. Внутри
2. Внутри
72

отрезка 0 x 2 имеется лишь одна критическая точка x 
 2
2
; соответствующей точкой отрезка AB является точка Q 
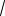 2;2 . Итак, наибольшее и наименьшее значения функции z на отрезке AB находятся среди ее значений в точках A, Q и B. Най-
2;2 . Итак, наибольшее и наименьшее значения функции z на отрезке AB находятся среди ее значений в точках A, Q и B. Най-
дем z Q z |
|
2;2 12 8 |
|
|
|
z B z 2;2 4; |
|
|||
|
2; |
|
||||||||
|
|
|
|
в) |
на дуге |
|
|
OB |
параболы y x2 2 |
имеем |
z |
3 |
x4 x3 |
0 x 2 . Решая уравнение z 3x3 3x2 |
0, по- |
||||||
|
||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
лучим x1 0 |
|
и |
x2 1; соответствующими точками параболы |
|||||||
являются точки O 0,0 и |
P1;1 2 . Таким образом, наибольшее |
|||||||||
и наименьшее значения функции z на дуге OB находятся среди ее значений в точках O, P и B. Найдемz P z 1;1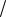 2 1
2 1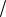 4
4
.
3) |
Сравнивая значения функции z 2x3 6xy 3y2 в точ- |
|
ках H , |
O, A, Q, B и P, получим решение задачи |
|
|
zнаиб z A 12, |
zнаим z H 1. |
Задачи и упражнения для самостоятельного решения
Решить задачи: [6], 3.25, 3.26, 3.27, 3.28, 3.35, 3.36, 3.37, 3.38.
Форма отчетности: устный опрос, контрольная работа.
ЗАНЯТИЕ № 19
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, ПРИВОДЯЩИЕСЯ К ОДНОРОДНЫМ
Литература: [12], c. 25-30; [13], c. 113-114; [20], c. 190-192; [33], c. 7-11.
73
Контрольные вопросы и задания
1.Какие уравнения первого порядка называются однородными?
2.Как решаются такие уравнения?
3.Укажите вид уравнений, приводящихся к однородным.
4.Какие два случая различают при решении таких уравнений? Каков алгоритм решения в каждом из этих случаев?
Пример решения задачи Пример. Решить дифференциальное уравнение
y 2 dx 2x y 6 dy 0.
Решение. Приведем уравнение к виду y |
y 2 |
. Это урав- |
|
||
|
2x y 6 |
|
нение можно привести к однородному. Сделаем подстановку
|
x u x0 , |
y v y0 . |
Подберем x0 |
и |
y0 |
так, чтобы |
|||||||||||||||||||
|
y 2 0 |
|
|
. Решая систему, находим x0 2, |
y0 2. То- |
||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|||||||||||||||||
2x0 y0 6 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
гда исходное уравнение принимает вид |
dv |
|
|
v |
, т.е. являет- |
||||||||||||||||||||
|
2u v |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du |
|
|
|||
ся |
однородным. Совершая |
подстановку v ut u , получим |
|||||||||||||||||||||||
t u |
dt |
|
|
|
ut |
. Далее, разделив переменные, получим урав- |
|||||||||||||||||||
du |
|
2u ut |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
t 2 |
|
du |
|
|
|
|
|
|
|
|
|
|
|
|||||
нение |
|
|
|
dt |
|
|
|
, проинтегрировав которое будем иметь |
|||||||||||||||||
|
t t 1 |
u |
|||||||||||||||||||||||
|
t |
2 |
|
|
C |
|
|
|
|
|
|
v |
y 2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
. Учитывая, что t |
|
|
|
записываем общий инте- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
t 1 |
u |
|
|
|
|
|
|
u |
x 2 |
|
|
|
y 2 2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
грал исходного дифференциального уравнения |
|
|
C . |
||||||||||||||||||||||
|
|
||||||||||||||||||||||||
x y 4 Разберите также решения примеров № 552, 553 [3].
74
Задачи и упражнения для самостоятельного решения
|
dy |
2 |
|
y 1 |
2 |
2) x y 2 dx 3x y 2 dy 0; |
||||
1) |
|
; |
||||||||
dx |
|
|||||||||
|
|
x y 2 |
|
|
|
3x 4y 2 |
|
|||
|
|
3) x y 1 dx 2x 2y 1 dy 0; |
4) y |
. |
||||||
|
|
|
||||||||
|
|
|
|
|
|
|
|
3x 4y 3 |
||
5) Определить кривые, у которых отрезок касательной от точки касания M до пересечения с осью Ox равен отрезку, отсекаемому касательной от оси Ox.
Форма отчетности: устный опрос, типовой расчет.
ЗАНЯТИЕ № 20
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ БЕРНУЛЛИ
Литература: [12], c. 30-35; [20], c. 192-194; [33], c. 11.
Контрольные вопросы и задания
1.Какие уравнения первого порядка называются линейными?
2.Какими методами решаются линейные дифференциальные уравнения?
3.В чем состоит метод Бернулли?
4.В чем состоит метод Лагранжа?
5.Какой вид имеет уравнение Бернулли?
6.Приведение уравнения Бернулли к линейным уравнениям?
7.Можно ли решать уравнение Бернулли, не приводя его к линейному виду?
Пример решения задачи Пример. Решить дифференциальное уравнение
75
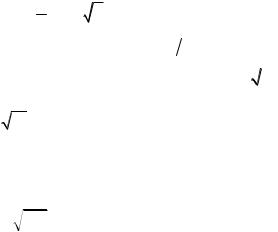
y 4 y x y . x
Решение.Это |
уравнение |
Бернулли с |
|
n 1 2. |
|
Полагаем |
||||||||
y x u x v x . |
|
|
|
|
|
|
|
4 |
|
|
|
|||
Получаем |
уравнение |
|
uv x uv |
|||||||||||
|
||||||||||||||
u v uv |
|
|||||||||||||
|
|
4 |
|
|
|
|
|
|
|
x |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||||
|
v x uv . Подберем такую функцию v x , |
|||||||||||||
или u v u v |
x |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
чтобы выражение в скобках было равно нулю, т.е. решим диф-
ференциальное уравнение v |
4 |
v 0. Находим |
v x4. Решаем |
|
|||
|
x |
|
|
затем уравнение u x4 x
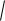 ux4 и получаем его общее решение
ux4 и получаем его общее решение
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
u |
|
ln |
|
|
Cx |
. Следовательно, общее решение исходного урав- |
|||||||||
|
|
||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
4 |
|
2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||
нения |
y |
uv |
|
x |
|
ln |
|
Cx |
. Нетрудно заметить, что y 0 |
явля- |
|||||
|
|
|
|||||||||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
ется особым решение исходного уравнения.
Задачи и упражнения для самостоятельного решения
Решить задачи: №№ 4038, 4039, 4041, 4043, 4044 [17].
Форма отчетности: устный опрос, типовой расчет.
ЗАНЯТИЕ № 21
УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА, НЕ РАЗРЕШЕННЫЕ ОТНОСИТЕЛЬНО ПРОИЗВОДНОЙ (КЛЕРО, ЛАГРАНЖА)
Литература: [12], c. 47-50; [33].
.
76

Контрольные вопросы и задания
1.Какие уравнения называются уравнениями Клеро?
2.Какая вспомогательная замена вводится при решении уравнений Клеро?
3.Что такое особое решение уравнения Клеро и каким свойством оно обладает?
4.Каков общий вид уравнений Лагранжа?
5.Какой вид уравнений более общий Клеро или Лагран-
жа?
6.Какой заменой решается уравнение Лагранжа?
7.Что такое особое решение уравнения Лагранжа?
8.Как ищется общее решение уравнения Лагранжа?
Примеры решения задач Пример 1. Решить уравнение y xy y 2.
Решение. Уравнение имеет вид (5.2), т.е. это уравнение Клеро. Положим y p. Тогда заданное уравнение принимает вид
y px p2. |
Продифференцировав |
его |
по x, |
имеем |
|
y p x p 2pp , |
или p x 2p 0с |
учетом y p. |
Если |
||
p 0, то |
p C |
и общее решение данного уравнения есть |
|||
y Cx C2 . Если |
x 2p 0, то получаем y p 2p p2 . Осо- |
||||
x 2p
бое решение данного уравнения .
y p2
Исключая параметр p, находим особое решение в явном виде
y x2 .
4
Пример 2. Решить уравнение y x 1 y y 2 .
Решение. Уравнение имеет вид (5.1), т.е. это уравнение Лагранжа. Положим y p. Тогда заданное уравнение принимает
77
вид |
|
|
y x 1 p p2. |
Продифференцировав его поx, |
имеем |
|||||||||||||||||||
y 1 p xp 2pp , |
|
откуда |
x 2p |
dp |
1 0. Из |
|
этого |
|||||||||||||||||
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
dx |
|
|
|
|
|||
уравнения получаем |
|
x 2p – линейное относительное x |
||||||||||||||||||||||
|
|
|||||||||||||||||||||||
|
|
|
|
dx |
|
|
|
|
|
|
dp |
|
|
|
|
|
|
|
|
|
||||
и |
|
уравнение. |
|
Решим |
его |
методом |
Бернулли. |
Полагая |
||||||||||||||||
dp |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x p u p v p , |
|
|
получаем |
u v uv uv 2p |
|
или |
||||||||||||||||||
|
|
|
|
|
|
|
|
Находим v, |
приравнивая скобку к нулю, |
|||||||||||||||
uv u v |
v 2p. |
|||||||||||||||||||||||
разделяя |
переменные |
|
и |
интегрируя: |
|
dv |
dp , |
|||||||||||||||||
|
|
|
||||||||||||||||||||||
|
v v 0, |
v |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ln |
|
v |
|
p, v e |
p |
. |
|
|
|
|
|
|
|
|
|
p |
2p. |
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
Тогда уравнение примет вид ue |
|
|
|||||||||||||||||||
Отсюда |
|
u 2 pepdp 2ep p 1 C. |
Учитывая, |
что |
y |
|||||||||||||||||||
x 1 p p2 , |
получим y 2 2p Ce p 1 p p2. |
Таким |
||||||||||||||||||||||
образом, общее решение уравнения имеет вид (в параметрической форме)
x 2 2p Ce p |
|
|
. |
|
|
y 2 2p Ce p 1 p p2 |
|
|
|
Особого решения данное уравнение не имеет.
Задачи и упражнения для самостоятельного решения
1) |
y xy y y 2; |
2) y xy 3 y 3; |
3) |
y x y 2 y 2; |
4) y x 1 y y 2 . |
|
|
78 |
Форма отчетности: устный опрос, самостоятельная работа.
ЗАНЯТИЕ № 22
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, ДОПУСКАЮЩИЕ ПОНИЖЕНИЕ ПОРЯДКА
Литература: [12], c. 56-66; [29], c. 196-198; [33], c. 12.
Указание. Перед изучением этой темы повторите все виды уравнений первого порядка и способы их решения.
Контрольные вопросы и задания
1.Какие уравнения второго порядка приводятся к уравнениям первого порядка?
2.Как решаются уравнения вида y f x ?
3. Как решаются уравнения вида y n f x ?
4.Как решаются уравнения видаF x,y ,y 0?
5.Как решаются уравнения вида F x, y n 1 , y n 0?
6.Как решаются уравнения видаF y,y ,y 0?
7.Можно ли понизить порядок дифференциального уравнения вида F y, y , y , , y n 0?
Примеры решения задач Пример 1. Найти частное решение дифференциального уравне-
ния y xe2x , удовлетворяющее заданным начальным услови-
ям y 0 1, y 0 2.
Решение. Интегрируя левую |
и правую |
части, находим |
||
y xe2xdx |
1 |
e2x 2x 1 C1. |
Повторное |
интегрирование |
|
||||
4 |
|
|
|
|
79 |
|
|
||

приводит к общему решению y 1e2x x 1 C1x C2. Учиты-
4
вая начальные условия, записываем систему уравнений для определения постоянных C1 и C2:
y 0 |
|
1 |
1 C |
2 |
1 |
|
C |
5 |
|
||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
4 . |
|||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
1 |
|
|
|
|
|
|
|
9 |
|
|
||
y 0 |
4 |
1 C1 |
2 |
|
C1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
4 |
|
|
|||||
Подставляя найденные значения постоянных в общее решение уравнения, получаем искомое частное решение
y |
1 |
e2x x 1 |
9 |
x |
5 |
. |
|
|
|
|
||
4 |
|
|
|
|
|
|
||||||
ч |
|
|
4 4 |
|
|
|
|
|
||||
Пример 2. Решить уравнение y |
|
|
|
|
|
|
||||||
|
y ctg x 2xsin x. |
|
0. |
|
||||||||
|
|
|
|
|
|
|
|
|
|
Поло- |
||
Решение. Данное уравнение имеет вид F x,y |
,y |
|
||||||||||
жим y p x . Тогда y |
p x . Получаем дифференциальное |
уравнение первого порядка |
p pctg x 2xsin x – линейное от- |
носительно неизвестной функции p x . Его общее решение p x2 C1 sinx, т.е. y x2 C1 sinx. Интегрируя это равен-
ство, найдем общее решение исходного уравнения y x2 C1 cosx 2xsin 2cosx C2 .
Пример 3. Найти частное решение дифференциального уравне-
ния 1 yy y 1 y 2 y , удовлетворяющее начальным ус-
ловиям y 0 y 0 1. |
|
|
|
|
|||
|
|
|
|
|
|
0. |
Подста- |
Решение. Данное уравнение имеет видF y,y ,y |
|
||||||
новка y p y , |
y |
dp |
p приводит |
его к |
виду |
||
|
|||||||
|
|
dy |
|
|
|
|
|
|
80 |
|
|
|
|
||
