
Учебное пособие 1431
.pdf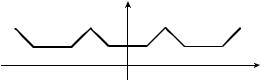
|
sink x |
|
1 |
|
sink x |
cosk x |
|
2 |
1 1 k |
|
|||
|
|
|
|
||||||||||
|
|
|
|||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
, |
|
|
k2 2 |
k2 2 |
||||||||||
|
k |
|
0 |
|
k |
|
|
1 |
|
||||
|
|
|
|||||||||||
|
|
|
|
||||||||||
2 |
|
|
|
|
1 |
|
|
|
2 |
|
|
||
bk f x sink xdx sink xdx xsink xdx
0 |
|
|
|
|
|
|
0 |
|
1 |
|
|
|
|
|
|
cosk x |
|
1 |
|
x |
cosk x |
sink x |
|
2 |
1 |
||||
|
|
|
||||||||||||
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k2 2 |
|
|
|
|||||||||
|
k |
|
0 |
|
|
k |
|
|
1 |
|
k |
|||
|
|
|
||||||||||||
|
|
|
|
|||||||||||
Подставляя найденные значения коэффициентов в ряд , окончательно получим
|
5 |
|
1 |
|
1 |
|
1 1 |
k |
f x |
|
|
|
|
||||
|
|
|
|
|
||||
4 |
k 1 k |
|
k |
|
||||
|
|
|||||||
cosk x sink x .
Пример 2. Функцию из примера 1 разложить в ряд Фурье по косинусам.
Решение. Продолжим данную функцию на отрезок 2,0 чет-
ным образом, а получившуюся функцию, в свою очередь, продолжим периодически (период T 2l 4) на всю числовую ось
(рис.15).
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
|
|
|
|
- |
|
- |
|
0 |
|
|
|
|
|
1 2 |
6 x |
||||||||
6 |
2 |
||||||||
Рис. 15
Вычисляем коэффициенты ряда Фурье по формулам
|
2 |
2 |
1 |
2 |
5 |
|
a0 |
|
|
f x dx dx xdx |
|
, |
|
2 |
2 |
|||||
|
|
0 |
0 |
1 |
|
|
|
|
|
101 |
|
|
|
a |
2 |
f x |
cos |
k x |
dx |
1 cos |
k x |
dx |
2 xcos |
k x |
dx |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
k |
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
k x |
|
1 |
|
2x |
|
|
k x |
4 |
|
|
k x |
|
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
sin |
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
2 2 |
|
|
|
|
||||||||||||||||
|
k |
|
2 |
|
0 k |
|
|
|
2 k |
|
2 |
|
1 |
||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
1 |
k |
|
|
|
|
|
k |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
. |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
k |
2 2 |
|
2 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Подставляя найденные значения коэффициентов в ряд , окончательно получим
|
5 |
|
4 |
|
1 |
|
|
k |
|
k |
k x |
||
f x |
|
|
|
|
|
|
1 |
|
cos |
|
cos |
|
. |
4 |
2 |
|
|
2 |
2 |
||||||||
|
|
k 1k2 |
|
|
|
|
|
|
|||||
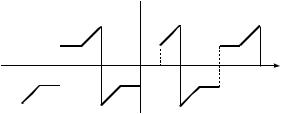
Пример 3. Функцию из примера 1 разложить в ряд Фурье по синусам.
Решение. Продолжим данную функцию на отрезок 2,0 не-
четным образом, а получившуюся функцию, в свою очередь, продолжим периодически (период T 2l 4) на всю числовую
ось (рис. 16).
y
2



1
-6 |
-2 |
0 |
1 2 |
6 x |
|
|
|
|
|
Рис. 16 Вычисляем коэффициенты ряда Фурье по формулам
b |
2 |
f x sin |
k x |
dx |
1 sin |
k x |
dx |
2 xsin |
k x |
dx |
|
|
2 |
2 |
|||||||
k |
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
1 |
|
|
|
|
102 |
|
|
|
|
|
|||
2 |
|
k x |
|
1 |
|
|
|
|
2x |
k x |
4 |
|
|
|
k x |
|
2 |
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
cos |
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|||
|
|
|
|
|
|
|
|
k2 2 |
|
|||||||||||||||||||
|
k |
2 |
|
0 |
|
|
|
|
k |
2 |
|
|
|
|
2 |
|
|
1 |
||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
2 |
|
|
4 |
|
1 k |
|
4 |
|
sin |
k |
. |
|
|
|
|
|||||||||
|
|
|
k |
k |
k |
2 2 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||
Подставляя найденные значения коэффициентов в ряд (10.5), окончательно получим
2 |
|
1 |
|
|
k |
|
2 |
|
k |
k x |
|||
f x |
|
|
|
1 2 |
1 |
|
|
|
sin |
|
sin |
|
. |
|
|
|
|
2 |
2 |
||||||||
k 1 k |
|
|
|
|
k |
|
|
||||||
Задачи и упражнения для самостоятельного решения
Решить задачи:№№ 12.495, 12.497, 12.500 [19].
Форма отчетности: устный опрос, контрольна
ЗАНЯТИЕ № 29
ПРИЛОЖЕНИЯ КРАТНЫХ ИНТЕГРАЛОВ
Литература: [12], c. 166-168, 179-189, 194-195, 199-200; [35].
Основные понятия
Приложения двойных интегралов
Пусть G - материальная бесконечно тонкая пластинка с поверхностной плотностью x, y . Тогда справедливы сле-
дующие формулы:
а) S dxdy - площадь плоской областиG ;
G
б) m x, y dxdy - масса пластинки;
G
103

в) Mx y x, y dxdy , |
My x x, y dxdy - стати- |
G |
G |
ческие моменты пластинки относительно осейOx и Oy ;
г) x |
My |
, |
y |
Mx |
- координаты центра тяжести |
|
|
||||
c |
m |
c |
m |
||
пластинки;
д) Ix y2 x, y dxdy , Iy x2 x, y dxdy - моменты
G G
инерции пластинки относительно осейOx и Oy ;
е) I0 Ix Iy x2 y2 x, y dxdy - момент инерции
G
пластинки относительно начала координат;
ж) если гладкая поверхность имеет уравнение z f x,y , то площадь части поверхности, проектирующей-
ся в областьG плоскости xOy, равна
|
|
|
z 2 |
|
z 2 |
|
||
Q |
1 |
|
|
|
|
|
dxdy; |
|
|
|
|||||||
|
|
x |
|
|
|
|
||
|
G |
|
y |
|
||||
|
|
|
|
|
|
|
|
|
з) объемV цилиндра, ограниченного сверху непрерывной поверхностью z f x,y , снизу плоскостью z 0 и
с боков прямой цилиндрической поверхностью, вырезающей на плоскости xOy область G , выражается интегралом
V f x, y dxdy.
G
Приложения тройных интегралов
Пусть T - материальное тело с объемной плотностью
x, y,z . Тогда справедливы следующие формулы:
а) V dxdydz - объем тела;
T
104
б) m x, y,z dxdydz - масса тела;
T
в) Myz x x, y,z dxdydz,
T
Mxz y x, y,z dxdydz, |
Mxy z x, y,z dxdydz - ста- |
|||||||||
T |
|
|
|
T |
|
|
|
|
|
|
тические моменты тела относительно координатных |
||||||||||
плоскостей yOz , xOz, xOy; |
|
|
|
|
|
|
|
|||
г) x |
Myz |
, |
y |
Mxz |
, |
z |
c |
|
Mxy |
- координаты |
|
|
|||||||||
c |
m |
c |
m |
|
|
m |
||||
центра тяжести тела; |
|
|
|
|
|
|
|
|
||
д) Iyz x2 x, y,z dxdydz, |
||||||||||
|
T |
|
|
|
|
|
|
|
|
|
Ixz y2 x, y,z dxdydz, |
Ixy z2 x, y,z dxdydz - мо- |
|||||||||
T |
|
|
|
T |
|
|
|
|
|
|
менты инерции тела относительно координатных плоско-
стей yOz , xOz, xOy;
е) Ix Ixz Ixy , Iy Iyz Ixy , Iz Iyz Ixz - мо-
менты инерции тела относительно осей координатOx, Oy ,
Oz; I0 Iyz Ixz Ixy x2 y2 z2 x, y,z dxdydz - мо-
T
мент инерции тела относительно начала координат.
Контрольные вопросы и задания
1.Как вычисляется площадь плоской области с помощью двойного интеграла?
2.Как вычисляется объем тела с помощью двойного интеграла?
3.Выведите формулу для вычисления площади гладкой по-
верхности z z x,y .
105
4.Как вычисляются площади поверхностей, заданных уравне-
ниями x x y,z y y x,z ?
5.Что такое поверхностная плотность вещества?
6.Как определить общее количество вещества в плоской области D (массу пластинки) с помощью двойного интеграла?
7.Как находятся моменты инерции плоской фигуры относительно координатных осей?
8.Как находится момент инерции плоской фигуры относительно начала координат? Покажите его связь с моментами инерции относительно координатных осей.
9.Как определяются координаты центра масс плоской фигуры?
10.Что такое статические моменты плоской фигуры? Как они вычисляются?
11.Как вычисляется объем тела тройным интегралом?
12.Как вычисляется масса пространственного тела?
13.Как найти моменты инерции пространственного тела отсительно координатных плоскостей?
14.Как найти моменты инерции пространственного тела относительно осей координат?
15.Как найти момент инерции пространственного тела отностельно начала координат?
16.Как определить статические моменты пространственного тела относительно координатных плоскостей?
17.Как определить координаты центра масс пространственного тела?
Примеры решения задач Пример1. Найти массу пластинки, ограниченной линией
x2 y2 2x, если ее плотность в любой точке пропорциональна квадрату расстояния от начала координат.
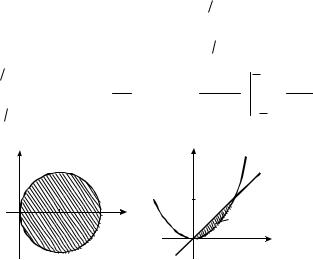
Решение. Линия x2 y2 2x или x 1 2 y2 1 является ок-
ружностью с центром в точке 1, 0 и радиусом 1 (рис. 17). По-
этому при вычислении интеграла удобно перейти к полярным
106
координатам. Подставляя в уравнение окружности полярные координаты, получим r 2cos . Плотность пластинки в по-
лярных координатах kr2 , где k - коэффициент пропорциональности. Таким образом, получаем
m x, y dxdy kr2rdrd k |
2 |
|
2cos |
|
||||||||
|
d |
|
r3dr |
|||||||||
D |
|
D |
|
|
2 |
|
|
0 |
|
|
||
|
2 |
|
3 |
|
sin4 |
|
|
|
|
3 k |
||
|
|
|
2 |
|
||||||||
|
cos4 |
|
|
|
||||||||
4k |
d k |
2 |
sin2 |
8 |
|
|
|
|
|
. |
||
|
2 |
|
|
|
|
|
2 |
|
2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
y |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
1 |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
1 |
2 |
x |
|
|
D |
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
x |
|
|
|
|
Рис. 17 |
|
|
Рис. 18 |
|
|
|
|
|
|||
Пример 2. Найти координаты центра масс однородной плоской фигуры, ограниченной кривыми y x и y x2 .
Решение. Построим область D, ограниченную данными кривыми (рис. 18). Вычислим массу пластинки, учитывая, что ее плотность x, y const
|
1 |
|
x |
|
1 |
|
|
x2 |
|
x3 |
1 |
|
|||
|
|
|
|
|
|
x x2 |
|
|
|
||||||
m |
dx |
dy |
dx |
|
|
|
|
|
|
. |
|||||
|
|
|
|||||||||||||
|
|
|
|
|
2 |
3 |
|
6 |
|
||||||
|
0 |
|
x2 |
|
0 |
|
|
|
0 |
|
|||||
Вычислим статические моменты пластинки относительно координатных осей Ox и Oy
107
|
|
|
|
|
|
|
|
1 |
x |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
Mx y x, y dxdy dx |
ydy |
|
dx x2 x4 |
|
|
, |
||||||||||||||||
|
15 |
|||||||||||||||||||||
D |
|
|
|
|
0 |
x2 |
|
2 |
0 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
1 |
|
x |
|
|
|
1 |
|
|
|
|
|
|
|
|
My x x, y dxdy xdx dy |
|
xdx x x2 |
|
|
||||||||||||||||||
12 |
|
|||||||||||||||||||||
|
D |
|
|
|
|
0 |
|
x2 |
|
|
|
0 |
|
|
|
|
||||||
Окончательно имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x |
My |
|
|
12 |
0,5; |
|
y |
Mx |
|
|
|
15 |
0,4. |
|
|
|
|
|||||
|
|
6 |
|
m |
|
|
6 |
|
|
|
|
|||||||||||
c |
|
m |
|
|
|
|
c |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
G |
0 |
|
1 y |
|
G |
0 |
|
|
|
|
y |
|
|
|
|
|||
|
|
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 19 |
|
|
|
Рис. 20 |
|
|
|
|
|
|
||||||||
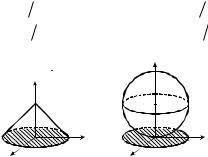
Пример3. Вычислить массу тела T , ограниченного по- |
||||||||||||||||||||||
верхностями |
z 0, |
z 12 x2 y2, |
если плотность |
тела |
||||||||||||||||||
x, y,z x y 2 z. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Решение. Область T |
|
представляет собой конус с основанием |
||||||||||||||||||||
G - круг радиуса 1 с центром в начале координат (рис. 19). При вычислении интеграла удобнее перейти к цилиндрическим ко-
ординатам r, ,z , в которых уравнение нижней половины ко-
нуса имеет вид z 1 r. Получаем
|
2 |
1 |
1 r |
r2 1 sin2 z dz |
m x, y,z dxdydz |
d rdr |
|||
T |
0 |
0 |
0 |
|
108

2 |
|
1 |
|
|
|
|
|
1 |
|
|
2 |
||
|
d r |
r2 1 r 1 sin2 |
|
1 r |
|
dr |
|||||||
2 |
|||||||||||||
0 |
|
0 |
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
1 |
1 sin2 |
1 |
|
|
|
11 |
|
|
|
|
|
|
|
|
|
d |
|
|
. |
||||
|
20 |
24 |
60 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
Пример 4. Вычислить момент инерции относительно оси Ox
однородного |
тела |
T |
плотности , |
ограниченного |
по- |
|||
верхностью x2 y2 |
z2 z. |
|
|
|
|
|||
Решение. |
Область |
T |
представляет собой шар, ограниченный |
|||||
сферой, |
уравнение |
которой |
удобно |
записать |
в |
виде |
||
x2 y2 z 1 2 2 1 4 (рис. 20), |
G - проекция шара на плос- |
|||||||
кость X,Y . |
При вычислении интеграла |
удобнее |
перейти к |
|||||
сферическим координатам r, , , в которых уравнение сферы
принимает вид r cos . Получаем |
x rcos sin |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
Ix y2 |
z2 dxdydz |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
y rsin sin |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
z rcos |
|
|
|
|
|
|
||||||
|
2 |
|
|
2 |
|
|
|
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
d |
sin d r2 sin2 sin2 cos2 r2dr |
||||||||||||||||||||||||||
|
0 |
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
d |
sin2 sin3 cos5 sin cos7 d |
|
||||||||||||||||||||||
5 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
sin2 |
|
|
cos3 2 |
|
sin4 |
2 |
|
cos8 |
|
|
|
2 |
|
||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
d |
|
|
|
|
|
|
cos2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
32 |
|
|
3 |
|
4 |
|
8 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
||
|
|
|
|
|
|
|
2 |
|
|
7 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
sin2 3 d |
|
. |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
120 |
120 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
109 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Пример 5. Найти моменты инерции Ix и Iy относительно осей
Ox и Oy пластинки с плотностью 1, ограниченной кривы-
ми xy 1, |
xy 2 , y 2x, |
x 2y и расположенной в первом |
||
квадранте. |
|
|
Ix y2dxdy |
|
Решение. |
Необходимо |
вычислить |
и |
|
|
|
|
G |
|
Iy x2dxdy . В декартовой системе координат, чтобы свести
G
каждый из этих двойных интегралов к повторному нужно область G (рис. 21) разбить на три части, поэтому удобнее перей-
ти к полярным координатам |
x rcos , y rsin . Тогда |
|||||||
изменяется от |
arctg |
1 |
до |
|
2 |
arctg2, а при каждом значе- |
||
|
||||||||
1 |
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
||
нии переменная r изменяется от r1 1 |
cos sin |
(зна- |
||||||
чения r |
на кривой xy 1, уравнение которой в полярных коор- |
||||||||||||||||||||||||||||||||
динатах в первом квадранте имеет вид |
r 1 |
|
|
|
|
|
|
) до |
|||||||||||||||||||||||||
|
|
|
cos sin |
||||||||||||||||||||||||||||||
r2 |
|
|
|
|
|
|
|
(значения r |
на кривой |
|
xy 2 ). Следо- |
||||||||||||||||||||||
|
2 |
cos sin |
|
|
|||||||||||||||||||||||||||||
вательно |
|
|
|
|
r2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
|
|
|
|
|
1 |
2 |
|
|
|
r24 r14 d |
|||||||||||||||||
Ix d |
r3 sin2 dr |
|
sin2 |
||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
|
|
|
1 |
r1 |
|
|
|
|
|
4 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
3 |
2 |
d |
|
|
|
3 |
|
|
arctg2 |
9 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
tg |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
4 |
|
cos |
|
|
4 |
|
|
arctg |
|
8 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2 |
r2 |
r3 cos2 dr |
3 |
|
|
|
arctg2 |
9 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
Iy d |
|
|
|
ctg |
|
|
|
|
|
|
. |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
8 |
|
||||||||||||||||||||
|
|
|
|
|
1 |
r1 |
|
|
|
|
|
|
|
|
4 |
|
|
|
arctg |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
110 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
