Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 1431

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

1.15 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1613 14 15 16 > Следующая >>>

1 n 1 2n 1

то

. Отсюда следует:а) в круге

z 2

z 1

n 1

f z

zn .

Это ряд Тейлора;б) в кольце

n 0 3

n 1

1 n zn

f z

. Ряд Лорана содержит

n 1

n 0

3 2n 1

как положительные, так и отрицательные степени z ;

1 n 1 2n 1 1

в) в кольце

f z

. Ряд Лорана содер-

3zn

n 1

жит только отрицательные степени z .

Пример 3. Определить характер особой точки z0 0 для функ-

ций: а) f z

, б) f z

cos

, в)

f z

1 e z

Решение. а)

sin z z

Используя

разложение

ряд

Тейлора

sin z z

, получим, что функция,

стоящая в зна-

z0 0

менателе дроби, имеет в точке

нуль третьего порядка.

Отсюда следует,

что функция

f z

имеет в точке

sin z z

z0 0 полюс третьего порядка.

б) Разложим

cos

в ряд

Лорана:

cos

2!z2

4!z4

1 n

. Отсюда видно, что главная часть ряда

2n !z2n

121

Лорана содержит бесконечно много членов. Поэтому для функ-

ции cos 1 точка z0 0 является существенно особой. z

в) Используя разложение в ряд Тейлора для функции e z в ок-

рестности

точки

z0 0,

получим

f z

1 e z

Лорановское

1 1 z

разложение функции в окрестности точки z0 0 не содержит

главной части, поэтому эта точка является устранимой особой точкой.

Задачи и упражнения для самостоятельного решения

1)Используя разложение основных элементарных функций, разложить в ряд по степеням z и указать области сходимости полученных рядов:

а) e z

sin2 z

z3e1 z

1 cosz

; б)

; в)

; г)

2) Доказать, что справедливы формулы:

z a

а)

при

z a

b a

;

b z

b a n 1

n 0

б)

при

z a

b a

b z

z a n 1

n 0

где a и b - заданные комплексные числа.

Указание: использовать при доказательстве разложение

функции 1 в ряд (геометрическую прогрессию). b z

3)Разложить в ряд Лорана следующие функции в указанных областях:

122

а)

f z

в кольце

и в кольце 1

;

z2 z

б)

f z

2z 3

в кольцах 0

z 1

1 и

z 2

z2 3z 2

f z

z i

в)

в кольце

2 1

г)

f z

в кольцах 2

3 и

z 2 z 3

Найти особые точки функции и определить их тип:

а) f z

; б) f

;

1 2

1 cosz

в)

f z z2 cos

;г) f

1 cosz

;

д) f z

z3 1

z 1

Форма отчетности: устный опрос,типовой расчет, коллоквиум.

ЗАНЯТИЕ № 36-37

ВЫЧЕТЫ И ИХ ВЫЧИСЛЕНИЕ. ОСНОВНАЯ ТЕОРЕМА О ВЫЧЕТАХ. ПРИМЕНЕНИЕ ВЫЧЕТОВ К ВЫЧИСЛЕНИЮ ИНТЕГРАЛОВ

Литература:[21], с. 132-137; [23], с. 70-81; [12], с. 172-179; [34], c. 66-75.

Контрольные вопросы и задания

1) Что называется вычетом функции f z относительно осо-

бой точки?

2) Чему равен вычет в устранимой особой точке и почему?

123

3)Как вычисляется вычет в простом и кратном полюсах?

4)Как находится вычет в существенно особой точке?

5)Сформулируйте основную теорему о вычетах. Как применяется теория вычетов к вычислению интегралов по замкнутым контурам?

6)Сформулируйте лемму Жордана. Как применяются вычеты при вычислении несобственных интегралов?

Примеры решения задач Пример 1. Найт и вычеты функции в ее особых точках.

f z z 1 z 2 2

Решение. Функция имеет две особые точки: z1 1 - простой полюс и z2 2 - полюс кратности 2. В случае простого полюса

вычет

вычисляется

по

формуле

Res f

z , z

lim f z z z

Для

z 1

получаем

Res f

z ,1

z z

lim

В случае полюса кратности

n 1

вычет вы-

z 1 z 2 2

числяется

по

формуле

Res f z , z

n 1 !

lim

dn 1

z z z

Для

n 2

получаем

z z0 dzn 1

Res f z ,

2 lim

z 2

z 1

Пример

2. Вычислить

вычет

f z e1 z

в точке z0 0

.Решение. Для функции e1 z

точка z0 0 является существенно

e1 z

особой,

так

как

Поэтому

2!z2

3!z3

124

Res f z , 0 c

где c

коэффициент ряда Лорана при

z 1.

Пример 3. Вычислить интеграл

z 2i

Решение. Подынтегральная функция

f z

имеет внут-

z 2i

ez 1

ри круга

одну особую точку z0 i

- полюс первого

порядка (рис.25). Воспользуемся формулой

f1 z

f1 z0 .

Получим

Res f

z , i

Res

, z0

f2 z0

f2 z

Далее воспользуемся основной теоре-

cos

z i

мой о вычетах.

Откуда получим

2 iRes f

z , i 2 i.

ez 1

z 2i

	\|
	z
	-
	2
		i
		\|
	z0=i	=
	z0=i	2
		2
	2

Рис. 25

Пример 4. Вычислить интеграл

		\|
			z
		\|
		=
		2
		z0=1 2		x
		Рис. 26
		2z 1 cos	z	dz .
		2z 1 cos	z 1	dz .
z	2		z 1
z	2

125

Решение. Подынтегральная функция f z 2z 1 cos z

	z		z 1
имеет внутри круга		2 одну особую точку	z0 1, которая

является существенно особой (рис. 26). Поэтому для вычисле-

ния вычета

точке

z0 1

применим

формулу

Res f z

,1 c

где

- коэффициент ряда Лорана при

z 1

Имеем

cos

cos 1

cos1 cos

sin1

z 1

sin

cos1 1

sin1

z 1

2! z 1

3! z

z 1

Так как 2z 1 2 z 1 1, то c 1 cos1 sin1 . Следователь-

но 2z 1 cos

dz 2 i cos1 sin1 .

z 1

Пример 5. Вычислить интеграл I

Решение. Введем функцию f z

которая на дейст-

1 4

вительной оси (z x) совпадает с подынтегральной функцией, которая является дробно-рациональной. Функция f z имеет в

верхней полуплоскости (Imz 0)								единственный полюс четве-
того	порядка	z	0	i. Поэтому				I 2 i Res f		z , i , где
			0
Res f z , i		1		1				5			5


									i. Отсюда I			.
		3!		z i	4			32		16
				z i			z i
							z i
						126

Задачи и упражнения для самостоятельной работы

Найти вычеты функции

f z

в ее особых точках:

а)

f z

;

б)

f z

sinz2

; в)

f z z3 sin

z 1 3 z 2

Вычислить интегралы: а)

dz, где C :

z2 1 z 2 2

tgzdz, где

z3 sin

б)

C :

в)

dz,

где

C :

1;г)

sin

dz , где C :

z 1

Вычислить несобственные интегралы:

cosxdx

xsin xdx

а)

x 1

dx ;

б)

;

в)

;

г)

x 1

x2 1

1 x2

4x 20

Форма отчетности:устный опрос, типовой расчет, коллоквиум.

ЗАНЯТИЕ № 38-39

ГРАФИЧЕСКОЕ ЗАДАНИЕ ФУНКЦИИ-ОРИГИНАЛА, НАХОЖДЕНИЕ ЕЕ ИЗОБРАЖЕНИЯ

Литература: [21], с. 251-259; [12], с. 413-422; 439-442; [28], с. 74-98, 142-150.

Контрольные вопросы и задания

1. Что такое единичная функция Хевисайда? Как она используется при построении функции-оригинала?

127

2.Как осуществляется переход к аналитическому выражению для функций-оригиналов, заданных графически?

3.Как находится изображение кусочно-аналитической функции-оригинала? Какие теоремы операционного исчисления при этом используются?

4.Как осуществляется изображение периодического оригинала?

5.Какие теоремы операционного исчисления при этом используются?

6.Какая функция называется полигональной функции?

7.В каких инженерных приложениях используется графическое задание функции-оригинала?

		Примеры решения задач
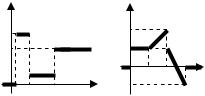
Пример 1. Найти изображение F(p)						функции				f (t), за-
данной графически (рис. 27).
Решение. Найдем аналитическое выражение для										f (t):
0,	t t1				0,			t t1
	t1 t t2
A,	t1 t t2		или	f (t)	A (t t1), t1 t t2						.
f (t)	t2 t t3		или	f (t)							.
B,	t2 t t3				B (t t2 ), t2 t t3
C, t t		3			C (t t		3	), t t	3
		3					3		3
Для всех t	0 получим

f(t) A (t t1) A (t t2) B (t t2) B (t t3) C (t t3)

A (t t1) (A B) (t t2) (C B) (t t3).

Пользуясь свойством линейности и теоремой запаздывания , находим искомое изображение:

F(p) Ae t1 p A B e t2 p C B e t3 p. p p p

128

				Рис. 27	Рис. 28
Пример 2. Найти изображение F(p) функции						f (t), за-
данной графически (рис. 28).
Решение. Найдем аналитическое выражение для						f (t):
b (t),					0 t a

	b	t (t a),			a t 2a


f (t) a			b
2				(t 2,5a) (t 2a),	2a t 3a

			a
					t 3a
0,

Для всех t 0 получим

129

f (t) b (t) b (t a) b t (t a) b t (t 2a)

		a		a
2	b	(t 2,5a) (t 2a) 2	b	(t 2,5a) (t 3a)

b (t) b (t a) (t a) b (3t 5a) (t 2a)

2 b (t 2,5a) (t 3a) b (t) b (t a) (t a)

3 b (t 2a) (t 2a) b (t 2a) a

2 b (t 3a) (t 3a) b (t 3a). a

Пользуясь свойством линейности и теоремой запаздывания , находим искомое изображение:

F(p)

e ap

e 2ap

e 3ap

ap2

e ap 1

e 2ap 1

e 3ap.

Пример 3. Найти изображение F(p) периодической функции f (t), заданной графически (рис. 29).

Рис. 29

Решение. Из рисунка видно, что период функции T 3. Найдем аналитическое выражение для f (t) на отрезке [0,T]:

130

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1613 14 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20221.15 Mб1Учебное пособие 1427.pdf
#
30.04.20221.15 Mб2Учебное пособие 1428.pdf
#
30.04.20221.15 Mб5Учебное пособие 1429.pdf
#
30.04.2022300.56 Кб1Учебное пособие 143.pdf
#
30.04.20221.15 Mб2Учебное пособие 1430.pdf
#
30.04.20221.15 Mб6Учебное пособие 1431.pdf
#
30.04.20221.15 Mб6Учебное пособие 1432.pdf
#
30.04.20221.15 Mб2Учебное пособие 1433.pdf
#
30.04.20221.16 Mб3Учебное пособие 1434.pdf
#
30.04.20221.16 Mб16Учебное пособие 1435.pdf
#
30.04.20221.16 Mб4Учебное пособие 1436.pdf