
Учебное пособие 334
.pdfМИНИСТЕРСТВО НАУКИ И ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Воронежский государственный технический университет»
Кафедра прикладной математики и механики
МАТЕМАТИКА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к практическим работам для студентов направления подготовки
54.03.01 «Дизайн» (профиль «Промышленный дизайн») заочной формы обучения
Воронеж 2021
1
УДК 51(07) ББК 22.1я7
Составители
канд. техн. наук О. А. Соколова, канд. физ.-мат. наук В. В. Горбунов
Математика: методические указания к практическим работам для студентов направления подготовки 54.03.01 «Дизайн» (профиль «Промышленный дизайн») заочной формы
обучения / |
ФГБОУ ВО «Воронежский государственный |
технический |
университет»; cост.: О. А. Соколова, В. В. Горбунов. |
– Воронеж: Изд-во ВГТУ, 2021. 27 с.
Приводится последовательность проведения практических занятий по дисциплине «Математика», разбираются опорные задачи, усвоение материала контролируется задачами для самостоятельного решения.
Предназначены для студентов направления подготовки 54.03.01 «Дизайн» (профиль «Промышленный дизайн») заочной формы обучения.
Методические указания подготовлены в электронном виде и содержатся в файле МУ_ПР_математика_54.03.01.pdf.
Ил. 4. Библиогр.: 2 назв.
УДК 51(07) ББК 22.1я7
Рецензент – А. В. Келлер, д-р физ.-мат. наук, доц. кафедры прикладной математики и механики ВГТУ
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
2
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1
Пример 1. Найти матричный многочлен AB 5C-3E , где
1 |
5 |
|
|
7 |
1 3 6 |
, В = |
4 |
1 |
|
, |
4 |
2 |
|||||
А = |
|
|
|
|
|
|
|
C |
|
|
. |
||
|
9 |
4 7 7 |
|
|
0 -8 |
|
|
1 |
2 |
|
|||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение.
Число столбцов матрицы А равно числу строк матрицы B , поэтому можно умножать матрицу А на матрицу B . По формуле перемножения матриц находим:
c11 a11b11 a12b21 a13b31 a14b41 7 1 1 4 3 0 6 2 23; c12 a11b12 a12b22 a13b32 a14b42 7 5 1 1 3 ( 8) 6 4 36; c21 a21b11 a22b21 a23b31 a24b41 9 1 4 4 7 0 7 2 39;
c |
|
9 5 4 1 7 ( 8) 7 4 21. |
23 |
36 |
||
22 |
Следовательно: АВ = |
|
|
. |
||
|
|
|
39 |
21 |
|
|
|
|
|
|
|
||
Матрица 5C |
4 |
2 |
|
20 |
|
10 |
, |
|
|
|
|
|||||
5 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
10 |
|
|
|
|
|
|
1 |
0 |
|
3 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
3E 3 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
3 |
|
|
|
|
|
|
|
|
|
|
|
||
Получаем матричный многочлен |
|
|
|
|
|
|
|
|
||||||||
AB 5C-3E |
|
23 36 |
|
20 |
|
10 |
|
|
3 |
0 |
0 |
46 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
44 |
8 |
|
|
39 |
21 |
|
5 |
10 |
|
|
0 3 |
|
|
||||||
|
Задачи для самостоятельного решения |
|
|
|
||||||||||||
|
|
|
|
|
|
|
3 |
5 |
|
|
|
2 |
3 |
|
|
|
1. Найти матрицу 2А+5В, |
если А |
|
|
|
, |
В |
|
|
|
|
|
|||||
|
1 |
|
|
|
. |
|
|
|||||||||
|
|
|
|
|
|
|
4 |
|
|
|
1 |
2 |
|
|
||
16 |
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ. |
8 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, В= |
1 . |
2. Найти матрицу АВ, если А |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ. АВ= |
. |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
Пример 2. Вычислить определитель третьего порядка |
|||||||||
|
|
4 |
1 |
3 |
|
, используя правило треугольников. |
|
|
|||||||
|
|
|
|
||||||||||||
|
|
1 |
2 |
1 |
|
|
|
||||||||
|
|
1 |
1 |
3 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Решение. |
|
|
|
|
|
||||
|
|
|
|
|
4 |
1 |
3 |
|
a11a22a33 a31a12a23 a13a21a32 (a31a22a13 a11a23a32 |
||||||
|
|
|
|
|
|||||||||||
|
|
1 |
2 |
1 |
|
||||||||||
|
|
|
|
|
1 |
1 |
3 |
|
|
|
|
|
|
|
|
a33a12a21) 4 2 3 1 1 1 3 1 1 (1 2 3 4 1 1 3 1 1) 24 1 3 (6 4 3) 15.
Задачи для самостоятельного решения
Вычислить определители третьего порядка
|
|
2 |
3 |
7 |
|
|
|
1. |
|
1 |
2 |
3 |
|
. Ответ: –73. |
|
|
|
2 |
1 |
4 |
|
|
|
2. |
|
1 |
17 |
7 |
|
. Ответ. 180. |
|
|
|
||||||
|
1 |
13 |
1 |
|
|
||
|
|
1 |
7 |
1 |
|
|
|
Пример 3. Решить систему уравнений:
x 2y z 4
3x 5y 3z 1.
2x 7y z 8
Решение. Расширенная матрица системы
4

1 |
2 |
1 |
|
4 |
|
|
|
|
-5 |
3 |
|
1 |
|
3 |
|
. |
||||
|
2 |
7 |
-1 |
|
8 |
|
|
|
|
||||
|
||||||
Умножаем каждый элемент 1-й строки на (-3) и складываем со 2-й строкой. Умножаем каждый элемент 1-й строки на (-2) и складываем
1 |
2 |
1 |
4 |
||
|
|
-11 |
0 |
|
|
с 3-й строкой. Получаем 0 |
-11 . |
||||
|
0 |
3 |
-3 |
0 |
|
|
|
||||
Умножаем каждый элемент 2-й строки на ( 3 ) и складываем с 3-й
строкой. Получаем |
|
|
|
11 |
|
|
|
|
|
|
|
1 |
2 |
1 |
4 |
|
|
|
-11 |
0 |
|
|
|
0 |
-11 . |
|
|||
|
0 |
-3 |
-3 |
|
|
0 |
|
|
|||
Тогда r(A) = r(A/B) =3 – система совместна. |
x 2y z 4 |
||||
|
|
|
|
||
Полученной матрице соответствует система |
|
-11y -11 , |
|||
|
|||||
|
|
|
|
|
-3z -3 |
|
|
|
|
|
|
откуда z = 1; y=1; x=1.
Задачи для самостоятельного решения
Решить системы уравнений методом Гаусса
x 3y 6z 10
1.2x y 2z 7 . Ответ: (1;1;2).
x y z 2
x 3y 4z 9
2.2x y z 1 . Ответ. (1;-2;1).
4x y 3z 5
Пример 4. Вершины пирамиды находятся в точках A(2,3,4),
B(4,7,3), С(1, 2,2), D( 2,0, 1). Вычислить:
5

а) площадь грани АВС; б) объем пирамиды ABCD; в) угол АВС;
г) Проверить, что векторы AB , AC, BC компланарны. Решение.
а) Площадь треугольника АВС находится как половина модуля
векторного |
произведения |
|
|
|
векторов |
|
|
AB 2,4, 1 |
и |
||||||||||||||||||
AC 1, 1, 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
AB AC |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
SABC |
|
1 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Находим векторное произведение векторов в координатном |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
k |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
представлении AB AC |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2 |
4 |
|
|
1 |
|
9i 5j 2k . |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Найдем длину векторного произведения |
|
|
|
|
|
||||||||||||||||||||||
|
AB AC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
( 9)2 (5)2 (2)2 |
110 |
. |
|
|||||||||||||||||||||
|
|
1 |
|
|
AB AC |
|
|
|
|
|
|
. |
|
|
|
|
|
||||||||||
Тогда SABC |
|
|
|
|
|
110 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
б) Сначала находим объем параллелепипеда, построенного на векторах AB 2,4, 1 , AC 1, 1, 2 и AD 4, 3, 5 , ко-
торый равен модулю смешанного произведения этих векторов. Смешанное произведение находим по формуле
AB,AC, AD AB AC ,AD |
2 |
4 |
1 |
|
1 |
1 |
2 |
|
|
|
4 |
3 |
5 |
|
10 3 32 4 12 20 11.
VABCD соответствует шестой части модуля смешанного про-
11
изведения трех векторов AB , ACи AD : VABCD 6 .
в) Косинус угла АВС находится по формуле
6

cos(ABC) BA,BC . BA BC
Имеем
cos(ABC) |
|
2 ( 3) 4 ( 5) 1 ( 1) |
|
|
|
|
25 |
|
0,92. |
|||
|
|
|
|
|
|
|
|
|
||||
( 2)2 ( 4)2 (1)2 ( 3)2 ( 5)2 ( 1)2 |
21 |
35 |
||||||||||
|
|
|
|
|
|
|||||||
По таблицам находим угол arccos(0,92) 230 .
г) Проверим выполнение условия компланарности векторов
AB , AC, BC
AB AC ,BC 0.
Вычисляем смешанное произведение AB,AC, AD
AB AC ,BC |
2 |
4 |
1 |
|
1 |
1 |
2 |
2 24 5 3 20 4 0. |
|
|
3 |
5 |
1 |
|
Следовательно, векторы компланарны.
Задача для самостоятельного решения. Вершины пирамиды находятся в точках A(3,5,4) , B(5,8,6) , С(1,9,9), D(6,4,8). Вычислить:
а) площадь грани АВС; б) объем пирамиды ABCD; в) угол АВС;
г) Проверить, что векторы AB , AC, BC компланарны.
Пример 5. Вершины пирамиды находятся в точках А(4,7,8),
B( 1,13,0) , С(2,4,9) и D(1,8,9).
Составить:
а) уравнения ребра АВ; б) уравнение грани АВС; в) уравнения высоты DE;
г) уравнения прямой, проходящей через точку D параллельно ребру АВ;
д) уравнение плоскости, проходящей через точку D перпендикулярно ребру АВ.
7

Вычислить:
е) длину ребра ВС;
ж) угол между ребром CD и плоскостью АВС; Решение.
Рис. 1
а) Уравнения ребра АВ могут быть получены как уравнения прямой, проходящей через две заданные точки А(4,7,8) и В(-1,13,0)
x 4 |
|
y 7 |
|
z 8 |
или |
x 4 |
|
y 7 |
|
z 8 |
. |
1 4 |
13 7 |
0 8 |
|
6 |
|
||||||
|
|
|
5 |
|
8 |
||||||
б) уравнение грани АВС получается как уравнение плоскости, проходящей через три заданные точки А(4,7,8), В(-1,13,0) и С(2,4,9)
x 4 |
y 7 |
z 8 |
0 или |
x 4 |
y 7 |
z 8 |
0. |
1 4 |
13 7 |
0 8 |
5 |
6 |
8 |
||
2 4 |
4 7 |
9 8 |
|
2 |
3 |
1 |
|
Раскрыв определитель, получим 6x 7y 9z 97 0 – уравнение
грани АВС.
в) Для получения уравнений высоты DE воспользуемся координатами точки D(1,8,9). В качестве направляющего вектора для DE
используем вектор нормали N 6, 7, 9 для плоскости АВС. Уравнения высоты DE запишутся в виде:
x 1 y 8 z 9
6 |
7 |
9 |
г) Для получения уравнений прямой, проходящей через точку D параллельно ребру АВ воспользуемся направляющим вектором q 5,6, 8 для прямой АВ:
8

x 1 y 8 z 9
5 |
6 |
8 |
д) Уравнение плоскости, проходящей через точку D(1,8,9) перпендикулярно ребру АВ записывается при использовании вектора
AB 5,6, 8 , как вектора нормали
5(x 1) 6(y 8) 8(z 9) 0 или 5x 6y 8 29 0.
е) Длину ребра BC находим как расстояние между точками
B(-1,13,0) и С(2,4,9):
BC 
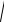 (2 ( 1))2 (4 13)2 (9 0)2
(2 ( 1))2 (4 13)2 (9 0)2 
 171.
171.
ж) Для нахождения угла между ребром CD и плоскостью осно-
вания АВС найдем sinφ (φ – угол между вектором CD 1,4,0 ) и
нормалью N 6, 7, 9 к плоскости АВС)
sin |
|
|
1 6 4 ( 7) 0 ( 9) |
|
|
|
|
|
34 |
|
|
0,64. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(6)2 ( 7)2 ( 9)2 |
|
( 1)2 (4)2 (0)2 |
17 |
166 |
||||||||||||||
|
|
|
|
|
|
|||||||||||||
arcsin(0,64) 390.
Задача для самостоятельного решения. Вершины пирамиды находятся в точках А(6,1,1), B(4,6,6) , С(4,2,0) и D(1,2,6).
Составить:
а) уравнения ребра АВ; б) уравнение грани АВС; в) уравнения высоты DE;
г) уравнения прямой, проходящей через точку D параллельно ребру АВ;
д) уравнение плоскости, проходящей через точку D перпендикулярно ребру АВ.
Вычислить:
е) длину ребра ВС;
ж) угол между ребром CD и плоскостью АВС;
Пример 6. Привести уравнение кривой к каноническому виду и построить линию, определяемую уравнением
x2 4y2 4x 8y 4 0 .
Решение. Выделяя полные квадраты, преобразуем левую часть уравнения. Имеем
9
(x2 2 2x 4 4) 4(y2 2y 1 1) 4 0 ; (x 2)2 4(y 1)2 4;
|
(x 2)2 |
|
(y 1)2 |
|
1. Вводя новые координаты X x 2,Y y 1, |
|||||||
4 |
1 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||||
получаем |
|
X 2 |
|
|
Y 2 |
1. |
|
|
||||
4 |
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
y |
Y |
|
|
|
|
|
|
|
|
|
|
|
1 |
O1 |
X |
|
|
|
|
|
|
|
|
|
|
O |
2 |
x |
|
|
|
|
|
|
|
|
|
|
|
Рис.2 |
|
|
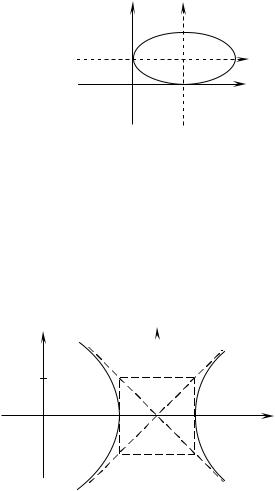
Пример 7. Привести уравнение кривой к каноническому виду и |
|||||||||||
построить линию, определяемую уравнением |
x2 y2 6x 8 0. |
|||||||||||
Решение. Выделяя полные квадраты, преобразуем левую часть уравнения. Имеем (x2 2 3x 9 9) y2 8 0; (x 3)2 y2 1.
Вводя новые координаты X x 3,Y y , получаем X 2 Y2 1 - уравнение гиперболы, для которой действительной осью является ось OX , а центр расположен в точке O1 3;0 .
y
Y
1
O1
O |
2 3 |
x X |
Рис. 3
10
