Методическое пособие 692

3

2

Рис. 2.21

Если силовой расчет механизма необходимо провести с учетом трения в кинематических парах, тогда расчет без учета трения является только первым приближением, по результатам которого определяются нормальные давления в парах, а затем

– приближенные значения сил трения на основании известных законов трения.

_

R03

_

R03

_

R03n

Рис. 2.22

59

3. МЕХАНИЗМЫ С ВЫСШИМИ ПАРАМИ. ЗУБЧАТЫЕ МЕХАНИЗМЫ

3.1.Зубчатые передачи

3.1.1.Общие сведения. Основная теорема зацепления.

Для того чтобы исключить проскальзывание и увеличить передаваемую мощность, используют зубчатые передачи. Они очень широко применяются в технике, их изучает наука, называемая теорией зубчатого зацепления.

Для того, чтобы передаточное отношение было постоянным, необходимо, чтобы профили зубьев удовлетворяли некоторым условиям.

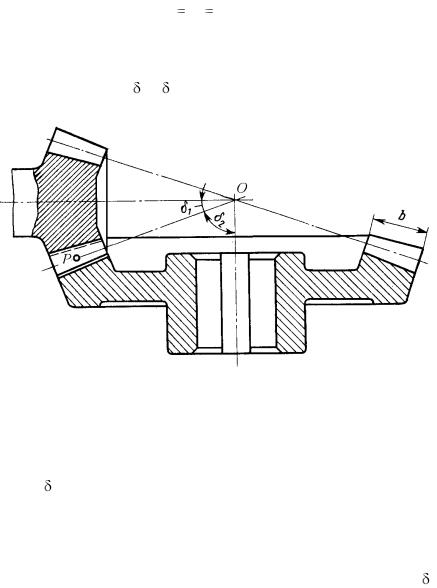
Пусть два звена, вращающихся вокруг осей О1 и О2, образуют в точке К высшую кинематическую пару (рис. 3.1).

n

K

q

P

n

Рис. 3.1

Очевидно, что относительная скорость должна лежать на касательной - к сопряженным профилям, т.к. в противном случае нормальная составляющая относительной скорости привела бы либо к отрыву звеньев друг от друга, либо к внедрению одного звена в другое. Из этого следует, что мгновенный центр скоростей в относительном движении лежит на нормали n-n, проведенной в точке контакта к сопряженным профилям. В то же время мгновенный центр скоростей должен лежать на пря-

60

мой О1О2, соединяющей оси вращения звеньев 1 и 2. Следовательно, мгновенным центром скоростей в относительном движении является точка Р, лежащая на пересечении нормали n-n и линии О1О2. В теории зубчатого зацепления эту точку называют

полюсом зацепления.

Из определения мгновенного центра скоростей следует, что относительная скорость в точке Р равна нулю, т.е.

VP1 = VP2.

Следовательно:

Отсюда передаточное отношение i12:

Иными словами, нормаль, проведенная в точке контакта к сопряженным профилям, делит межосевое расстояние в отношении, обратно пропорциональном отношению угловых скоро-

стей. Это – основная теорема зацепления. Для того, чтобы пере-

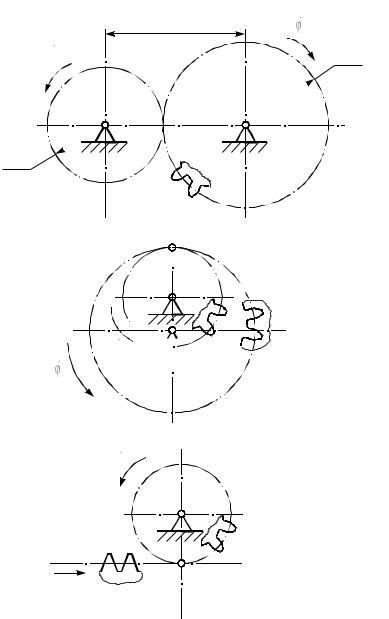
даточное отношение i12 было постоянным, необходимо, чтобы полюс зацепления занимал постоянное положение. В этом случае центроидами в относительном движении будут являться окружности, которые в теории зубчатого зацепления называются начальными окружностями. Все размеры, относящиеся к начальным окружностям, помечают индексом w, например: rw1, rw2

– радиусы начальных окружностей (рис. 3.2, а).

Радиусу начальной окружности rw пропорциональна длина начальной окружности и, следовательно, число зубьев z, которое может на ней разместиться. Поэтому для передаточного отношения справедливо выражение:

61

a)

P

O1

q O2

б)

q

O1

в)

Рис. 3.2

62

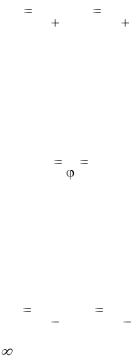
Знак «минус», стоящий перед отношением чисел зубьев ведомого и ведущего колеса, показывает, что в передаче внешнего зацепления ведущее и ведомое колеса вращаются в противоположные стороны, а передаточное отношение – отрицательное.

Расстояние между осями вращения зубчатых колес называют межосевым расстоянием и обозначают аw. В случае внешнего зацепления

Учитывая, что rw1 = O1P, rw2 = O2P, из (3.2) и (3.4) полу-

чим:

Для того чтобы уменьшить габариты передачи, используют колеса внутреннего зацепления: одно колесо вставляется внутрь другого (рис. 3.2, б). В этом случае направление вращения ведущего и ведомого колес совпадает, поэтому передаточное отношение – положительное:

Межосевое расстояние равно разности радиусов начальных окружностей:

Если rw2 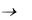, то начальная окружность превращается в начальную прямую, а зубчатое колесо – в зубчатую рейку. В

этом случае получают зубчато-реечную передачу (рис. 3.2, в).

63

Поскольку в полюсе зацепления относительная скорость равна 0, то VP1 = VP2, тогда

Для передачи вращения между валами с пересекающимися осями используют конические колеса (рис. 3.3). Чаще всего угол между осями 1 + 2 = 900 (такие передачи называют ортогональными), но возможны и другие углы.

Рис. 3.3

В передачах с коническими колесами существует мгновенная ось (OP) – геометрическое место точек тел, имеющих в данный момент нулевую относительную скорость. Если мгновенную ось ОР, наклоненную к оси вращения шестерни под углом 1, вращать вокруг оси 1, получится коническая поверхность – подвижная аксоида (поверхность, образованная мгновенной осью в локальной системе координат, связанной со звеном 1 или 2, называют подвижной аксоидой). Аналогично при вращении мгновенной оси ОР вокруг оси II получим коническую поверхность с половиной угла при вершине, равной 2 (вторая подвижная аксоида). Подвижные аксоиды в теории

64

зубчатых зацеплений называются начальными конусами. Зубья колес располагают вблизи начальных конусов, а поверхности вершин и впадин имеют ту же форму, что и начальные конусы.

В качестве главного профиля зубьев цилиндрических зубчатых колес, применяемых в машиностроении, наибольшее распространение получил эвольвентный профиль. Плоская эвольвента окружности представляет собой траекторию любой точки прямой линии, перекатываемой без скольжения по эволюте, т.е. по основной окружности радиуса rb (рис. 3.4).

Прямая линия, перекатываемая по основной окружности, называется производящей прямой. Рассмотрим свойства эвольвенты окружности.

1.Нормаль к эвольвентам (прямая КС) касается основной окружности, причем точка касания (С) является центром кривизны эвольвент.

2.Все эвольвенты одной основной окружности эквидистантны, и расстояние KD между ними равно длине дуги К0D0.

3.Каждая ветвь эвольвенты вполне определяется радиусом основной окружности и положением начала отсчета эвольвентного угла.

D0

O

C

rb

Рис. 3.4

При эвольвентном зацеплении изменение межосевого расстояния не влияет на значение передаточного отношения вследствие неизменности радиусов основных окружностей.

65

3.1.2. Геометрические элементы зубчатых колес

Геометрия зубчатого колеса зависит в первую очередь от размеров и формы инструмента. Поэтому стандартизация параметров инструмента, воспроизводящего эвольвентный профиль зубчатого колеса, необходима с технической и экономической точек зрения. За основу стандарта форм и размеров зубчатого колеса принят теоретический исходный контур

(ТИК, рис. 3.5).

Рис. 3.5

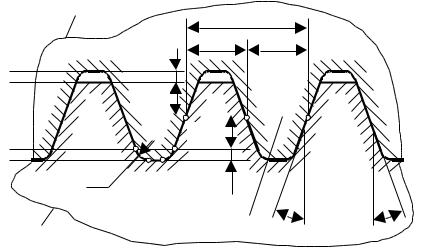
Размеры теоретического исходного контура установлены государственным стандартом. Базовая линия теоретического исходного контура, по которой толщина зуба равна ширине впадины, называется его делительной прямой. Расстояние между одноименными профилями соседних зубьев по делительной или по любой другой параллельной ей прямой называют шагом зубьев р исходного контура.

Если форма инструмента повторяет форму ТИК, а делительная прямая является начальной прямой, то начальная окружность нарезаемого колеса касается делительной прямой ТИК. Как уже отмечалось ранее, подвижные центроиды катят-

66

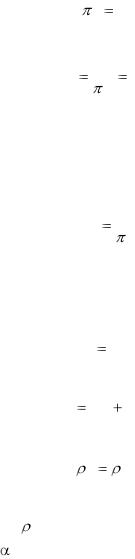
ся друг по другу без скольжения, поэтому шаг зубьев по начальной окружности колеса должен быть равен шагу зубьев ТИК. Если z – число зубьев нарезаемого колеса, то длина окружности – подвижной центроиды колеса равна:

где d – диаметр подвижной центроиды колеса:

Подвижную центроиду колеса при его зацеплении с рейкой называют делительной окружностью. Делительная ок-

ружность делит зуб на делительную головку и делительную ножку. В выражении (3.11) введен основной параметр зубчатого зацепления – модуль m:

Модуль измеряется в миллиметрах и может принимать только значения, оговоренные государственным стандартом. В долях модуля задаются все линейные размеры контура: высо-

та делительной головки

бокового профиля зуба является вырожденной эвольвентой ок-

67

ружности при rb 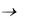) и осью симметрии зуба называется уг-

лом профиля исходного контура. Государственный стандарт устанавливает следующие значения параметров исходного контура:

Исходным производящим контуром называется такой,

который заполняет впадины теоретического исходного контура, как отливка заполняет форму (рис. 3.5, ИПК). При этом между прямой вершин теоретического исходного контура и прямой впадин исходного производящего контура сохраняется радиальный зазор с*m. Это делается для того, чтобы поверхность впадин инструмента, образованного на базе исходного производящего контура, не участвовала в процессе нарезания зубьев.

3.1.3.Кинематика зубчатых механизмов

снеподвижными осями

Передаточное отношение одной пары цилиндрических колес

где для внешнего зацепления берется отрицательный знак (колеса вращаются в разные стороны).

Рис. 3.6

68