Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Методическое пособие 503

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

1.94 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 159 10 11 12 13 14 15 > Следующая >>>

3.18. Метод подбора построения частного решения неоднородного уравнения

Рассмотрим линейное неоднородное дифференциальное уравнение

y(n) + a		y(n −1)	+ ... + a y′ + a y = f (x).		(3.27)
n −1			1	0
Коэффициенты an −1,..., a1, a0 −	постоянные действительные числа,				f (x) −
непрерывная на отрезке [a,b] правая часть.
Общее решение этого уравнения имеет вид
y(x) = C1 y1 (x) + C2 y2 (x) + ... + Cn yn (x) + y (x),					(3.28)

где C1 , C2 ,...,Cn − произвольные постоянные, y1 (x), y2 (x),..., yn (x) − фундамен- тальная система решений однородного уравнения, y (x) − частное решение

неоднородного уравнения.

Частное решение y (x) можно найти методом подбора, если правая часть

уравнения (3.27) −	квазимногочлен −		функция вида
	f (x) = eα x (M	m	(x) cos(β x) + N	n	(x)sin(β x)).	(3.29)
		m		n
Здесь M m (x)	− многочлен степени m , Nn (x) − многочлен степени n, α и β −

действительные числа.

Метод подбора вычисления частного решения линейного неоднородного уравнения с квазимногочленом в правой части состоит в том, что частное решение уравнения отыскивают в виде

y (x) = eα x (P (x)cos(β x) + Q (x)sin(β x))xr ,		(3.30)
k	k

где Pk (x) и		Qk (x) − многочлены				степени		k = max(n, m) с неизвестными
коэффициентами,
P (x) = p xk + p		k −1	xk −1	+ ... + p x + p , Q (x) = q			k	xk + q	k −1	xk −1 + ... + q x + q .
k	k			1	0	k				1	0
	Для того чтобы найти неизвестные коэффициенты многочленов										Pk (x) и

Qk (x) , подставляем (3.30) в уравнение и приравниваем в правой и левой части полученного равенства коэффициенты при одинаковых функциях:

eα x cos(β x), eα x sin(β x), xeα x cos(β x), xeα x sin(β x),

(3.31)

x2eα x cos(β x), x2eα x sin(β x),..., xk eα x cos(β x), xk eα x sin(β x).

Полученная таким образом система 2k + 2 уравнений относительно 2k + 2 неизвестных имеет единственное решение.

Метод подбора применяется к ограниченному, но достаточно широкому классу правых частей, поскольку квазимногочленами являются функции вида

M k (x), M k (x)eα x ,			M k (x)cos(β x), M k (x)s in(β x),
eα x (M	m	(x)cos(β x) + N		n	(x)sin(β x)).

Метод подбора вычисления частного решения линейного неоднородного уравнения с квазимногочленом в правой части состоит в следующем. Рассмотрим правую часть уравнения и записываем число α + β i . Затем составим характеристическое уравнение однородного уравнения и найдем его корни. Возможны два случая: среди корней характеристического многочлена нет корня, равного числу α + β i (нерезонансный случай) и среди корней характеристического многочлена есть r корней, равных числу α + β i (резонансный случай).

Рассмотрим нерезонансный случай (среди корней характеристического многочлена нет корня, равного числу α + β i ). Тогда частное решение уравнения найдем в виде

y (x) = eα x (Pk (x)cos(β x) + Qk (x)sin(β x)),

где Pk (x) и Qk (x) − многочлены степени

k = max(n, m)

неизвестными

коэффициентами,

P (x) = p xk + p

k −1

xk −1 + ... + p x + p ,

Q (x) = q

xk + q

k −1

xk −1 + ... + q x + q .

Для того чтобы найти неизвестные коэффициенты многочленов

Pk (x)

Q (x) ,

подставим

y (x) = eα x (P (x)cos(β x) + Q (x)sin(β x))

уравнение

приравняем коэффициенты при функциях (3.31). Доказано, что полученная таким образом система 2k + 2 уравнений относительно 2k + 2 неизвестных имеет единственное решение.

Рассмотрим резонансный случай (среди корней характеристического многочлена есть r корней, равных числу α + β i ). Тогда частное решение уравнения будем искать в виде (3.30). Для того чтобы найти неизвестные коэффициенты многочленов Pk (x) и Qk (x) , подставляем (3.30) в уравнение и приравниваем коэффициенты при одинаковых функциях (3.31).

Пример № 3.20. Уравнением колебаний называют линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами:

y′′ + ω02 y = F cosω x.

Однородное уравнение y′′ + ω02 y = 0 описывает свободные колебания материальной точки с частотой ω02 . Неоднородное уравнение – колебания материальной точки под действием внешней периодической силы F cosω x, частота которой равна ω.

Найдём общее решение уравнения колебаний в случае, когда частота свободных колебаний не совпадает с частотой внешней вынуждающей силы.

Характеристическое уравнение однородного уравнения λ 2 +ω02 = 0 имеет пару комплексно сопряжённых корней λ1,2 = ±iω0 .

Фундаментальную систему решений однородного уравнения образуют функции cosω0 x, sinω0 x. Общее решение однородного уравнения имеет вид

y(x,C1,C2 ) = C1 cosω0 x + C2 sinω0 x.

Правая часть уравнения –	имеет	вид	eα x (M	m	(x)cos(β x) +
+Nn (x)sin(β x)) = F cosω x, у которого	α = 0,	β = ω,		m
+Nn (x)sin(β x)) = F cosω x, у которого	α = 0,	β = ω,	M m (x) = M 0 = F,
Nn (x) = 0, α + β i = iω.

Поскольку ω ¹ ω0 , среди корней характеристического уравнения нет корня,

равного корню характеристического уравнения.

Будем искать частное решение неоднородного уравнения y (x) в виде

y (x) = Acosω x + B sinω x.

Продифференцируем дважды частное решение и подставим в уравнение:

y′ = − Aω sinω x + Bω cosω x, y′′ = − Aω 2 sinω x − Bω 2 sinω x,

y′′ + ω 2 y = − Aω 2 sinω x − Bω2 sinω x + ω 2 ( Acosω x + Bωsinω x) =
0					0
= A(−ω 2 + ω	2 )cosω x + B(−ω2 +			ω	2 )sinω x = F cosω x.
0				0
Приравняв коэффициенты в левой и правой части уравнения
A(−ω 2	+ ω 2 )cosω x + B(−ω2				+ ω 2 )sinω x = F cosω x ,
	0				0
получим систему линейных уравнений

	cosω x	A(−ω	2		2
	cosω x	A(−ω		+ ω0 ) = F ,
	sinω x			+	ω 2 ) = 0,
	sinω x	B(−ω 2		+	ω 2 ) = 0,
					0
					0

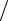
решение которой B = 0, A = F (−ω2 + ω		2 ) , и тогда частное решение неоднород-
		0
ного уравнения
	F
y (x) =			cosω x.
y (x) =	(−ω 2	+ ω 2 )	cosω x.
		0

Теперь можно записать общее решение неоднородного уравнения:

	F
y(x) = C1 sinω0 x + C2 cosω0 x +		cosω x.
	(−ω 2 + ω 2 )
	0

3.19. Уравнение Эйлера

Уравнением Эйлера называется однородное дифференциальное уравнение

вида

xn y	(n) + a	n −1	xn −1 y	(n −1) + ... + a xy′ + a xy = 0.		(3.32)
		n −1		1	0

Коэффициенты an −1,..., a1, a0 − постоянные действительные числа.

Если функция y(x) − решение уравнения Эйлера, то функция Cy(x) тоже является решением уравнения.

Уравнение Эйлера заменой x = et сводится к однородному линейному

уравнению с постоянными коэффициентами. Выполним замену x = et , перейдём к новой переменной t = ln x :

x = et , t = ln x,

= e−t y(x) = y(et ) = g(t),

xy¢ = x

= x

y¢¢ = x

2 d 2 y

= x

2 d

= x

2 d dg

= x

d 2 g

dx dx

dx dt

…

d k −1g

xk y(k ) = xk

d k y

d k g

+ αk , k −1

+ ...

+ αk ,1

dxk

dt k

dtk −1

xn y(n) = xn

d n y

d n g

+ αn, n −1

d n −1g

+ αn,1

+ ...

dxn

dtn

dtn −1

Здесь αij

− коэффициенты,

которые легко вычисляются при последователь-

ном дифференцировании.

После подстановки в уравнение имеем
	d n g	%		d n −1g	%	dg	%

	dtn + αn,n −1 dt n −1 +				... + αn,1	dt	+ α0 g = 0.
Решим это однородное линейное уравнение с постоянными коэффици-
ентами − его общее решение			g = g(t,C1,C2 ,...Cn ).			Вернувшись к переменной x ,
получим общее решение уравнения Эйлера (3.32):

y(x,C1,C2 ,...Cn ) = g(ln x,C1,C2 ,...Cn ).

Пример № 3.21. Найдём общее решение уравнения Эйлера

x2 y¢¢ + 3xy¢ + y = 0.

Выполним замену x = et , перейдём к новой переменной t = ln x :

x = et , t = ln x,

= e−t y(x) = y(et ) = g(t),

xy¢ = x

= x

y¢¢ = x

2 d 2 y

d dy

2 d

2 d 2 g 1

d 2 g

= x

dx dx

После подстановки в уравнение имеем: g′′ + 2g′ + g = 0. Составим и решим характеристическое уравнение

		2λ 2 + 2λ + 1 = 0, λ = λ = -1.
					1				2
Фундаментальную систему решений однородного уравнения образуют
функции e−t и te−t , а общее решение g = g(t,C ,C						2	) = C e−t						+ C			te−t .
				1		2			1				2
Вернувшись к переменной			x ,	t = ln x, получим общее решение уравнения
Эйлера:	y(x,C ,C ) = C e− ln x								ln xe− ln x ,
	y(x,C ,C ) = C e− ln x				+ C			2	ln xe− ln x ,
		1	2	1				2
y(x,C ,C		) = C x−1		+ C x−1 ln x = C						1	+ C			ln x	.
y(x,C ,C		) = C x−1		+ C x−1 ln x = C							+ C				.
1	2	1		2				1 x				2		x

Задачи и упражнения

3.1. Решить уравнения, допускающие понижения порядка:

1) yIV = sin 2x; 2) y′′′ = e4 x+1; 3) y′′ − y′ = 0; 4) y′′ − ( y′)2 + y′( y − 1) = 0. x

3.2. Решить линейные однородные дифференциальные уравнения:

1) y′′ − 5 y′ + 6 y = 0;	2) y′′ − 6 y′ + 25 y = 0;
3) y′′ − 9 y′ = 0;	4) y′′′ − 2 y′′ − y′ + 2 y = 0.

3.3. Решить линейные неоднородные дифференциальные уравнения:

1) y′′ − 3y′ + 2 y = 5 + ex ;	2) y′′ − 2 y′ + y = 2;
3) y′′ + 4 y = sin 2x + cos 2x;	4) y′′ − 3y′ = x2 − 2x + 4.

4.СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

4.1.Системы обыкновенных дифференциальных уравнений.

Основные понятия

Рассмотрим систему обыкновенных дифференциальных уравнений n-го порядка

Y '= F ( x ,Y )

	y			y '
	1			1
Y = y2		,	Y '= y2 '		,
K				K

yn			yn '


или	dY	= F ( x,Y ), где							(4.1)
или		= F ( x,Y ), где							(4.1)
	dx				( x ,y1 ,y2 ,K ,yn )
			f1		( x ,y1 ,y2 ,K ,yn )
F ( x) =			f		( x ,y ,y		,K ,y		)
F ( x) =				2	1	2		n	.
					K
			f		( x ,y ,y		,K ,y
			f	n	( x ,y ,y	2	,K ,y	n	)
				n	1	2		n

Задачей Коши для этой системы называется следующая задача:

найти такое решение Y = Y ( x) системы (4.1), что Y ( x0 ) = Y0 , где Y0 − некоторый постоянный вектор.

Вектор-функция Y = Y ( x,C ) , зависящая от произвольного вектора C , назы-

вается общим решением системы (4.1), если:

−при любом векторе C вектор-функция Y ( x,C ) является решением системы;

−какова бы ни была начальная точка ( x0 ,Y0 ) , существует такой вектор C(0) ,

что Y (x(0) ,C (0) ) = Y0 .

Пример № 4.1. Дана система обыкновенных дифференциальных уравнений 4-го порядка относительно двух неизвестных функций x = x (t ) и y = y (t ) :

x ''+ y +' x = 0
							0.
x '+ y ''=
Запишем эту систему в канонической форме: x ''= − y −' x
						y ''= −x '.
Обозначив x (t ) = z1 (t ) , y (t ) = z2 (t ) ,							x '(t ) = z3 (t ) , y '(t ) = z4 (t ) , можно
записать систему в нормальной форме:
dz					= z3 ,
		1

dt
	dz2				= z ,

dt			4

	dz3			= −z4 − z1 ,

dt

	dz4				= −z3 .

dt

И, безусловно, удобнее всего записывать систему в векторной форме:

Z '= F (t ,Z ), где

(t )

z '(t )

(t )

'(t )

(t )

Z = Z (t ) =

, Z '= Z '(t ) =

, F (t, Z ) =

−z

(t )

z '(t )

(t ) − z

(t )

(

3 (

)

z ' t

−z

4.2. Фазовое пространство. Фазовые траектории

Рассмотрим систему обыкновенных дифференциальных уравнений n-го

порядка (4.1),

и пусть

вектор-функция

Y = Φ ( x)

−

решение

системы,

определённое на промежутке [a,b].

Множество

точек

Φ ( x) , x [a;b] есть

кривая в

пространстве

R n . Эту

кривую называют фазовой траекторией системы (или просто траекторией, или

фазовой кривой), а пространство RY n , в котором расположены фазовые

траектории, называют фазовым пространством системы.

Интегральная кривая системы определяется уравнением Y = Φ ( x) , x [a,b] и изображается в (n +1) - мерном пространстве RY , xn+1 .

Фазовая траектория − это проекция интегральной кривой на пространство

RY n .

На рис. 4.1, а изображена интегральная кривая в пространстве RY , x2+1 и фазовая траектория в пространстве RY 2 изображена на рис. 4.1, б:

Рис. 4.1. а) - интегральная кривая; б) - фазовая траектория системы

Пример № 4.2. Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений 2-го порядка, записанную в нормальной и в векторной форме:

y1 '= 3y1 + 4y2 ,					y1 (0) = 1,				3y1 + 4y2				1
y	2	'= − 3y − 3y	2	,	y	2	(0) = 1,	Y =	− 3y	− 3y	2	;	Y (0) = 1 .
	2	1	2			2			1		2

Решение этой задачи можно также записать в обычной аналитической и в векторной форме:

	1	( x) = 3 sin	3x + cos 3x,
y		( x) = 3 sin	3x + cos 3x,

		( x) = − 3 sin
y2		( x) = − 3 sin		3x,

					x + cos
	3 sin			3	x + cos
Y =
		−	3 sin 3x
		−	3 sin 3x

3x .

На рис. 4.2, а приведено изображение соответствующей интегральной кривой, расположенной в пространстве RY , x2+1 , а на рис. 4.2, б - фазовая

траектория, расположенная в пространстве RY 2 .

Рис. 4.2. а) интегральная кривая; б) фазовая траектория для системы из примера 4.2

4.3. Существование и единственность решения задачи Коши

Рассмотрим систему обыкновенных дифференциальных уравнений n-го порядка (4.1).

Пусть задана задача Коши для этой системы

Y '= F ( x ,Y ) ,

Y ( x		) = Y ,	(4.2)
	0	0

где Y0 − некоторый постоянный вектор.

Справедлива следующая теорема о существовании и единственности решения задачи Коши.

Теорема 4.1. Пусть в области D из Rn+1 непрерывны все компоненты вектора правой части F ( x,Y ) и их частные производные по Y :

	f1		( x, y1 , y2 ,K, yn )
	f	2	( x, y , y	2	,K, y	n	)
F ( x,Y ) =		2	1	2		n		,
F ( x,Y ) =			K					,
	f		( x, y , y		,K, y
	f	n	( x, y , y	2	,K, y	n	)
		n	1	2		n

∂f j ( x, y1 , y2 ,K, yn ) , i = 1, 2,K, n; j = 1,2,K, n. ∂yi

Тогда, какова бы ни была начальная точка ( x0 ,Y0 ) ≡ ( x0 , y10 , y20 ,K, yn0 ) D , существует такой отрезок [ x0 - h; x0 + h] , что задача Коши (4.2) имеет

единственное решение.

Важно понимать, что эта теорема имеет локальный характер: существование решения Y = Y ( x) гарантируется лишь в достаточно малой окрестности точки x0

( h > 0 может оказаться достаточно малым).

Важно также понимать, что теорема содержит только достаточные условия существования и единственности решения − при нарушении условий теоремы задача Коши может иметь или не иметь решений, может иметь несколько решений.

Пример № 4.3. Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений второго порядка:

dy
dy		= y1			(0) = 0,
	1		,	y1
			,
dx
					(0) = 0.
dy2		= y1 y2 ,		y2	(0) = 0.
		= y1 y2 ,
dx

Легко проверить, что задача имеет два решения:

0		y		( x)			x2

						y1	( x) = 4	, x ³ 0,
Y =		и Y =	1		, где	y1	( x) = 4	, x ³ 0,
	0			0				x < 0.
							0,	x < 0.

Нарушение единственности объясняется тем, что нарушены условия теоремы существования и единственности решения задачи Коши. Действительно,

	¶f1 ( x, y1, y2 )			¶		=
			=		y1		1	.

	¶y			¶y			2 y
1				1			1
Частная производная функции f1 ( x, y1 , y2 )		по y1 разрывна в начальной точке (0,0,0) .

4.4. Интегрирование систем дифференциальных уравнений методом исключения

Системы дифференциальных уравнений n-го порядка можно решать сведением к уравнению n-го порядка. Такой метод решения систем называется

методом исключения.

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 159 10 11 12 13 14 15 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20227.69 Mб5Методическое пособие 50.doc
#
30.04.2022314.43 Кб6Методическое пособие 50.pdf
#
30.04.20221.93 Mб16Методическое пособие 500.pdf
#
30.04.20221.93 Mб2Методическое пособие 501.pdf
#
30.04.20221.93 Mб4Методическое пособие 502.pdf
#
30.04.20221.94 Mб6Методическое пособие 503.pdf
#
30.04.20221.94 Mб4Методическое пособие 504.pdf
#
30.04.20221.94 Mб3Методическое пособие 505.pdf
#
30.04.20221.95 Mб7Методическое пособие 506.pdf
#
30.04.20221.95 Mб12Методическое пособие 507.pdf
#
30.04.20221.95 Mб21Методическое пособие 508.pdf