
- •1. Система сил на площині
- •1.1.Короткі теоретичні відомості
- •1.2. Довільна система сил
- •1.3. Задачі для самоконтролю
- •2. Кінематичний аналіз плоских систем і визначення реакцій з’єднань
- •2.1.Короткі відомості про кінематичний аналіз
- •2.3. Схеми задач для самостійного розв’язування
- •3. Розрахунок плоских статично визначуваних ферм
- •3.1.Короткі теоретичні відомості
- •3.3. Схеми задач для самостійного розв’язування
- •4. Статично визначувані просторові ферми
- •4.1. Короткі теоретичні відомості
- •4.3. Задачі для самостійного розв’язування
- •5. Розрахунок шарнірно-консольної балки на нерухоме навантаження
- •5.1.Основні теоретичні відомості
- •5.3. Задачі для самостійного розв’язування
- •6. Розрахунок тришарнірних арок
- •6.1 Короткі теоретичні відомості
- •6.3. Схеми задач для самостійного розв’язування
- •7. Статично визначувані рами
- •7.1. Короткі теоретичні відомості
- •7.2.Розрахунок простої рами
- •7.3.Розрахунок складеної рами
- •7.4. Розрахунок рами із замкненим контуром
- •8. Розрахунок на рухоме навантаження
- •8.1. Короткі теоретичні відомості
- •8.2. Лінії впливу для двоопорної балки
- •8.3. Лінії впливу для консольної балки
- •8.4. Навантаження ліній впливу
- •8.5. Лінії впливу для шарнірно–консольної балки
- •8.6. Лінії впливу в фермах
- •8.7. Лінії впливу в шпренгельних фермах
- •8.9. Задачі для самостійного розв’язування
- •9. Обчислення переміщень у стержневих системах
- •9.1. Короткі теоретичні відомості
- •9.6. Задачі для самостійного розв’язування
- •10. Розрахунок статично невизначуваної рами методом сил
- •10.1. Короткі теоретичні відомості
- •10.2. Розрахунок рами методом сил
- •10.3. Розрахунок симетричної рами методом сил
- •10.4. Задачі для самостійного опрацювання
- •11. Статично невизначувані ферми
- •11.1.Короткі теоретичні відомості
- •11.3. Задачі для самостійного опрацювання
- •12. Нерозрізна балка
- •12.1.Основні теоретичні відомості
- •12.2. Розрахунок статично невизначуваної балки на постійне навантаження методом трьох моментів
- •12.3.Розрахунок нерозрізної балки на тимчасові навантаження методом моментних фокусів
- •12.5. Задачі для самостійного опрацювання
- •13. Метод переміщень
- •13.1.Короткі відомості про метод переміщень
- •13.2.Розрахунок несиметричної рами в канонічній формі
- •13.3. Розрахунок несиметричної рами в розгорнутій формі
- •13.4. Розрахунок симетричної рами на симетричне навантаження
- •13.6. Задачі для самостійного опрацювання
- •14. Метод скінченних елементів для стержневих систем
- •14.1.Основні положення методу скінченних елементів
- •14.3. Розрахунок шарнірно-стержневої системи методом скінченних елементів
- •14.4. Схеми для самостійного розв’язування
- •15.Розрахунок рам на стійкість
- •15.1. Короткі теоретичні відомості
- •15.3. Розрахунок на стійкість симетричної рами
- •15.4. Задачі для самостійного розв’язування
- •16. Динамічний розрахунок рам
- •16.1.Короткі відомості про розрахунок на динамічні дії
- •16.4. Задачі для самостійного опрацювання
- •17. Розрахунок стінової панелі методом скінченних елементів
- •17.1. Короткі відомості про розрахунок стінової панелі
- •17.3. Задачі для самостійного розв’язування
- •18. Навчальний програмний комплекс АСИСТЕНТ
- •18.1. Основні характеристики
- •18.2. Запуск комплексу АСИСТЕНТ
- •18.3. Керування роботою комплексу
- •18.4. иконання розрахункових робіт
- •19.1. Основні характеристики
- •19.3. Завантаження ОК SCAD і основні елементи керування
- •19.4. Основні етапи створення розрахункової схеми в ОК SCAD
ДО ЗМІСТУ ПОСІБНИКА
14. Метод скінченних елементів для стержневих систем
14.1.Основні положення методу скінченних елементів
14.2. Приклад розрахунку плоскої рами
14.3. Розрахунок шарнірно-стержневої системи методом скінченних елементів
14.4. Схеми для самостійного розв’язування
14. Метод скінченних елементів для стержневих систем
14.1.Основні положення методу скінченних елементів
Основна ідея методу скінченних елементів полягає в тім що конструкція представляється на бором окремих фрагментів – скінченних елементів які взаємодіють між собою в скінченній кіль кості точок – вузлах
Пружно-деформований стан скінченно-елементної дискретної моделі конструкції характери зується переміщеннями та реакціями визначеними у вузлах Зусилля і переміщення у будь-якій точці визначаються як функції вузлових переміщень
Скінченно-елементна модель стержневої системи
Перший етап розрахунку стержневої системи за методом скінченних елементів полягає в дис кретизації тобто в переході від її розрахункової схеми до дискретної моделі Вихідна розрахун кова схема розбивається на окремі стержні скінченні елементи і вузли Скінченні елементи по винні являти собою прямолінійні стержні постійної жорсткості на яких може бути розташоване рівномірно розподілене зовнішнє навантаження Криволінійні стержні апроксимуються декілько ма прямолінійними елементами Аналогічно апроксимуються стержні що мають змінну жорст кість або ті до яких прикладено нерівномірно розподілене навантаження Така схема споруди на зивається її дискретною або скінченно-елементною моделлю (СЕМ .
Вузлами дискретної моделі вважають точки поєднання двох або більше окремих стержнів ступінчатої зміни жорсткості стержнів
прикладення зосереджених зовнішніх сил або моментів ступінчатої зміни інтенсивності розподіленого навантаження опорні вузли
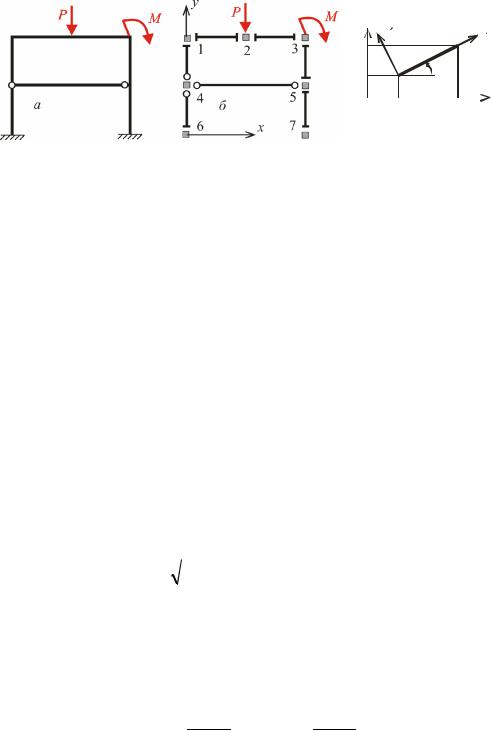
Перехід від розрахункової схеми до дискретної моделі показано на рис 14. Розрахункова схема рами рис 14.1.а перетворена на СЕМ рис 14.1,б Вузли дискретної моделі в даному прикладі пронумеровані в довільному порядку Для позначення будь-якого скінченного елемента до статньо вказати номери вузлів які він поєднує
2
|
|
y y |
j x |
|
|
yj |
|||
|
|
|
||
|
|
i |
|
|
|
yi |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
xi |
x j |
|
Рис 14.1 |
|
Рис 14.2 |
||
Для визначення взаємного розташування вузлів |
їх кінематичних і статичних характеристик |
|||
вводиться загальна для всього об’єкту система декартових координат xy |
яка називається загаль- |
|||
ною або глобальною.
езпосередньо з кожним стержнем пов’язується його власна система координат x’y’ якою зру чно користуватися для аналізу напружено-деформованого стану стержня Така система координат
називається місцевою або локальною Початок місцевої системи координат пов’язується з тим вузлом що має менший номер ю точку називають початком стержня а точку яка розташована на протилежному кінці стержня його кінцем Вісь x’ спрямовують вздовж стержня від його по чатку до кінця а вісь y’ перпендикулярно до стержня причому прямий кут відкладається від осі
x’ проти ходу годинникової стрілки рис 14. На рисунку початок стержня позначено літерою а кінець літерою j Такі позначення будуть застосовуватися і надалі
Довжина стержня обчислюється через координати вузлів на початку і на кінці за формулою
|
|
|
|
|
|
|
|
|
|
|
l |
|
(x |
j |
x )2 |
(y |
j |
y )2 , |
(14.1) |
||
|
|
|
i |
|
|
i |
|
|||
де xi , x j , yi , y j координати відповідних вузлів у глобальній системі координат |
|
|||||||||
Тригонометричні функції кута |
повороту локальної системи координат стержня відносно |
|||||||||
глобальної системи координат усієї дискретної моделі можуть бути обчислені за формулами |
|
|||||||||
sin |
yj |
yi ; |
cos |
xj xi . |
(14.2) |
|||||
|
|
|
|
l |
|
|
|
|
l |
|
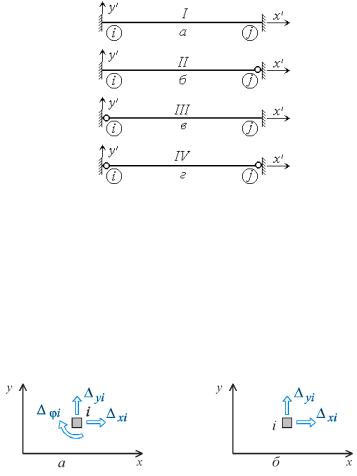
У плоскій дискретній моделі можна виділити чотири типи скінченних елементів які відрізня ються граничними умовами тобто способами примикання до вузлів
жорсткі вузли на початку і на кінці стержня рис 14.3,а);
жорсткий вузол на початку і шарнірний вузол на кінці стержня рис 14.3,б);
шарнірний вузол на початку і жорсткий вузол на кінці стержня рис 14.3,в);
шарнірні вузли на початку і на кінці стержня рис 14.3,г).
3
Рис 14.3
узлові характеристики дискретної моделі
Вузли дискретної моделі можуть бути характеризовані із статичного і кінематичного погляду Кінематичними характеристиками є вузлові переміщення а статичними вузлові навантаження і вузлові реакції
Рис 14.4
удь-який вільний жорсткий вузол i дискретної моделі має три ступеня вільності тобто мож |
|
|||
ливість двох поступальних xi , yi і одного кутового переміщення i цього вузла рис 14.4,а |
і |
|||
величини можуть бути записані у вигляді вектора |
|
|
|
|
i xi |
yi |
i |
T . |
|
Положення шарнірного вузла на площині характеризується тільки поступальними переміщен нями xi , yi рис 14.4,б Тому шарнірний вузол має два ступеня вільності і відповідно вектор пе реміщень такого вузла матиме дві компоненти
|
i |
|
T . |
|
|
xi yi |
Сукупність усіх вузлових переміщень дискретної моделі рис 14.5,а складає вектор вузлових переміщень
|
|
|
... |
i |
... |
T . |
|
1 |
2 |
|
|
7 |
або

4
|
x1 |
y1 |
1 |
x2 |
y2 |
2 , |
, |
x7 |
y7 |
7 .T . |
Рис
Для практичних розрахунків зручно використовувати наскрізну нумерацію компонентів вузло вих переміщень у межах всієї моделі рис 14. Тоді вектор вузлових переміщень матиме вигляд
1 2 3  4 5 6
4 5 6  , ,
, , 18 19 20 .T
18 19 20 .T
Деякі переміщення вузлів можуть бути відомі з граничних умов задачі Так у даному прикладі
15 |
|
16 |
|
17 |
|
18 |
|
19 |
20 0. |
Отже невідомими є переміщення |
|
1, |
2 , |
... , |
14 |
Вектор |
після вилучення нульових елемен |
||
тів набуває остаточного вигляду |
|
|
|
|
|
|
|
|
|
{ 1 2 3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 12 13 14}T |
|
Компоненти вектора вузлових переміщень становлять основні невідомі методу скінченних елементів у формі методу переміщень хня кількість характеризує кількість ступенів вільності дискретної (скінченно-елементної) моделі
Статичною характеристикою вузлів дискретної моделі є вузлові навантаження В кожному ву злі i припускається можливість дії трьох компонентів зовнішніх зосереджених силових дій Fxi
сила яка спрямована вздовж осі x загальної системи координат Fyi сила яка діє вздовж осі y;
F i зосереджений момент Сукупність зосереджених дій у жорсткому вузлі i може бути записа на у вигляді вектора
Fi Fxi Fyi F i T ,
а сукупність вузлових навантажень які можуть діяти на всі вузли дискретної схеми рис 14.5,б), вектором

|
|
|
|
|
|
|
|
5 |
|
|
|
|
T |
Fx1 |
Fy1 F 1 |
Fx2 Fy2 F 2 |
T |
F F1 |
F2 ... Fi |
... F7 |
|
, , Fx7 Fy7 F 7 . |
||||
Вектор F можна представити як суму двох векторів |
|
|||||||
|
|
|
|
|
|
F F Q, |
(14.3) |
|
де F вектор зовнішніх сил що безпосередньо діють на вузли його компоненти дорівнюють від |
||||||||
повідним зовнішнім силовим діям Q |
вектор реактивних сил що передаються на вузли з боку |
|||||||
тих стержнів на які діє |
розподілене навантаження |
Компоненти цього вектора необхідно попере |
||||||
дньо визначити звівши розподілене на стержнях навантаження до |
вузлових сил |
|||||||
При розв’язанні практичних задач компоненти зазначених векторів також мають наскрізну нумерацію яка відповідає нумерації вузлових переміщень
F {F1 |
F2 |
F3 |
F4 |
F5 |
F6 |
F7 |
F8 |
F9 |
F10 |
F11 |
F12 |
F13 |
F14}T ; |
F {F1 |
F2 |
F3 |
F4 |
F5 |
F6 |
F7 |
F8 |
F9 |
F10 |
F11 |
F12 |
F13 |
F14}T ; |
Q {Q1 |
Q2 |
Q3 |
Q4 |
Q5 |
Q6 |
Q7 |
Q8 |
Q9 |
Q10 |
Q11 |
Q12 |
Q13 Q14}T . |
|
На шарнірний вузол вузол ферми можуть діяти дві компоненти зовнішніх навантажень які дорівнюють проекціям зовнішніх сил прикладених до вузла Отже для шарнірного вузла сукуп ність зосереджених дій у вузлі i може бути записана у вигляді вектора
Fi |
Fxi Fyi |
T , |
е одна статична характеристика вузлів – вузлові реакції Під впливом зовнішніх дій вузли |
||
дискретної моделі переміщуються а стержні |
які їх поєднують деформуються Між вузлами і сте |
|
ржнями виникають реакції взаємодії що зумовлені тільки переміщеннями вузлів Сумарні реакції всіх стержнів які приєднуються до вузла i зобразимо у вигляді двох зосереджених сил що орієн товані вздовж осей глобальної системи координат всієї моделі і зосередженого моменту Позна
чимо ці реакції через Rxi , Ryi , R i . |
|
|
Реакції які передаються на вузол i з боку стержнів |
і на стержні що приєднуються до вузла |
|
однакові за величиною але спрямовані в протилежних напрямах |
Звичайно для реактивних сил з |
|
якими вузли діють на стержні за додатні приймають |
напрями |
які збігаються з додатними |
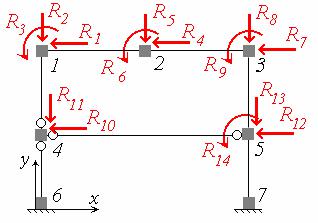
напрямами вузлових переміщень Тоді реакції які передаються на вузли з боку стержнів будуть спрямовані у протилежних напрямах рис 14.6).
6
Рис 14.6
Сукупність реакцій для жорсткого вузла i можна записати у вигляді вектора
Ri {Rxi Ryi R i}T .
кщо вузол шарнірний то вектор вузлових реакцій має дві компоненти
Ri Rxi Ryi T
Вузлові реакції всієї дискретної моделі утворюють вектор вузлових реакцій
R {R1 R2 ... Rn}T .
При розв’язанні практичних задач використовується наскрізна нумерація реакцій причому їх ні номери повинні збігатися з номерами відповідних переміщень
R {R1 R2 R3  R4 R5 R6
R4 R5 R6  R7 R8 R9
R7 R8 R9  R10 R11
R10 R11 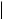 R12 R13 R14}T .
R12 R13 R14}T .
Матриця жорсткості дискретної моделі
У лінійно деформованих об’єктах між вузловими реакціями і вузловими переміщеннями що їх зумовлюють існує лінійна залежність Так для дискретної моделі з n ступенями свободи
R1 |
|
K1,1 |
1 |
|
K1,2 |
2 |
|
|
K1,n |
n ; |
|
R2 |
|
K2,1 |
1 |
|
K2,2 |
2 |
|
|
K2,n |
n ; |
(14.4) |
|
|
|
|
|
|
|
|
|
|
|
|
Rn |
Kn,1 1 |
Kn,2 2 |
|
Kn,n n |
|
||||||
або в матричній формі
R K . |
(14.5) |
|
|
|
|
7 |
Тут R – вектор вузлових реакцій |
– вектор вузлових переміщень |
K – матриця жорсткості |
||
дискретної моделі |
|
|
|
|
|
K1,1 |
K1,2 |
K1,n |
|
K |
K2,1 K2,2 |
K2,n |
(14.6) |
|
|
|
. |
||
|
Kn,1 |
Kn,2 |
Kn,n |
|
удь-який елемент Ki, j матриці – це вузлова реакція Ri яка зумовлюється вузловим перемі
щенням j 1 за умови що всі інші вузлові переміщення дорівнюють нулю Зазначимо що голо
вні елементи матриці жорсткості – це істотно додатні числа Ki,i |
0 а сторонні елементи симетри |
||||||||||
чні відносно головної діагоналі Ki, j K j,i при i |
j ). |
|
|
|
|
|
|||||
Рівняння рівноваги вузлів дискретної моделі |
|
|
|
|
|
|
|||||
З умов рівноваги вузлів дискретної моделі ( Fx |
0, |
Fy 0, |
|
M 0 одержимо систе |
|||||||
му рівнянь яка в матричній формі має вигляд |
|
|
|
|
|
|
|
|
|
||
|
|
|
R F 0 , |
|
|
|
|
(14.7) |
|||
де 0– нульовий вектор |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
0 |
0 T . |
|
|
|
|
|
З урахуванням співвідношення |
14. система рівнянь (14. |
набуває вигляду |
|||||||||
|
|
|
K |
F 0 |
|
|
|
|
(14.8) |
||
або в координатній формі |
|
|
|
|
|
|
|
|
|
|
|
K1,1 1 |
K1,2 |
2 |
|
K1,n |
n |
F1 |
0; |
|
|||
K2,1 |
1 |
K2,2 |
2 |
|
K2,n |
n |
F2 |
0; |
(14.9) |
||
|
|
|
|
|
|
|
|
|
|
|
|
Kn,1 1 Kn,2 |
2 |
Kn,n |
n Fn 0. |
|
|||||||
Невідомими в рівняннях 14. |
є переміщення вузлів |
коефіцієнти величини вузлових реак |
|||||||||
цій вільні члени вузлові навантаження |
|
|
|
|
|
|
|
|
|
||
к було зазначено будь-який коефіцієнт матриці жорсткості Ki, j |
дискретної моделі являє со |
||||||||||
бою вузлову реакцію Ri що обумовлена вузловим переміщенням |
j |
1 На цій підставі для обчи |
|||||||||
8
слення коефіцієнтів матриці жорсткості необхідно почергово надавати одиничні переміщення вуз лам дискретної моделі і знаходити сили які при цьому передаватимуться на вузли Величини цих сил визначаються елементами відповідних матриць жорсткості окремих стержнів
Кінцеві характеристики стержнів
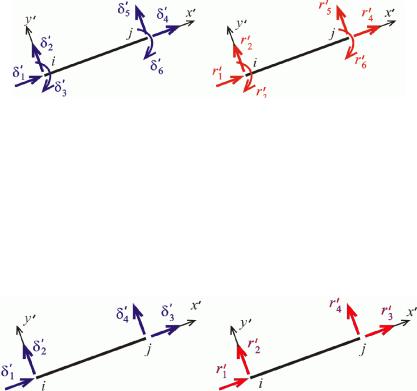
У процесі деформування споруди її вузли отже і кінці стержнів переміщуються внаслідок чо го на кінцях виникають реакції взаємодії стержнів з вузлами дискретної моделі і кінцеві реакції і кінцеві переміщення можуть бути визначені в локальній або в глобальній системі координат По значення і додатні напрями кінцевих переміщень і реакцій в локальній системі координат для сте ржня який жорстко примикає до вузлів зображено відповідно на рис 14.7,а і рис 14.7,б.
Рис 14.7
Необхідно звернути увагу на те що кінцеві переміщення і кінцеві реакції нумеруються в суво ро визначеному порядку
Аналогічно позначення і додатні напрями кінцевих переміщень і реакцій в локальній системі координат для стержня який примикає до вузлів шарнірно зображено відповідно на рис 14.8,а і
рис 14.8,б.
Рис 14.8
Таким чином кінцеві переміщення в локальній системі координат на початку i стержня який жор стко приєднується до вузлів можуть бути записані у вигляді матриці-стовпця вектора
|
|
1 |
|
|
T . |
|
2 |
|
1 2 |
||
i |
|
|
3 i |
||
|
|
3 |
i |
|
|
Аналогічно можна представити вектор кінцевих переміщень на кінці j стержня

9
4 |
|
j 5 |
{ 4 5 6}Tj . |
6 |
j |
Повний вектор переміщень скінченного елемента e в локальній системі координат матиме ви гляд
|
|
|
|
T |
T . |
e |
|
|
i |
j e |
1 2 3 4 5 6 e |
Так само можна записати вектор кінцевих реакцій стержня в локальній системі координат
|
|
|
T |
|
|
|
T |
re |
|
ri |
rj e |
r1 |
r2 |
r3 r4 |
r5 r6 e . |
Для стержня який приєднується до вузлів шарнірно стержень ферми вектори кінцевих пе реміщень і реакцій в локальній системі координат матимуть вигляд
|
|
|
|
T |
|
|
T |
e |
|
i |
j |
e |
1 |
2 |
3 4 e |
|
|
|
T |
|
|
|
T |
re |
|
ri |
rj e |
r1 |
r2 |
r3 |
r4 e |
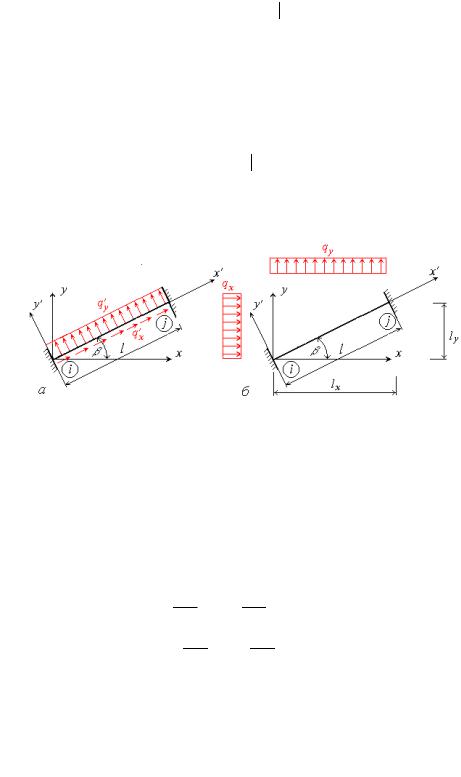
Кінцеві переміщення і реакції можуть бути представлені у вигляді компонентів які являють собою проекції відповідних величин на осі глобальної і локальної систем координат Позначення і додатні напрями зазначених компонентів для стержня жорстко прикріпленого до вузлів представ лено на рис 14.9,а,б а для стержня який приєднується до вузлів шарнірно на рис 14.9,в,г.
Нумерація цих величин також суворо фіксована і аналогічна нумерації в локальній системі ко ординат
Рис 14.9
10
Кінцеві переміщення і кінцеві реакції в глобальній системі координат можуть бути представ лені у вигляді векторів
для стержня жорстко прикріпленого до вузлів
|
e |
|
i |
|
j |
T |
1 |
2 |
3 |
4 |
T ; |
|
|
|
e |
6 e |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
T |
re |
|
|
ri |
rj e |
r1 |
r2 |
r3 |
r4 |
r5 |
r6 e . |
|
для стержня прикріпленого до вузлів шарнірно
|
|
|
|
|
T |
|
|
T |
e |
|
|
i |
j |
e |
1 |
2 |
4 4 e |
|
|
|
|
T |
|
|
|
T |
re |
|
ri |
rj e |
r1 |
r2 |
r3 |
r4 e |
|
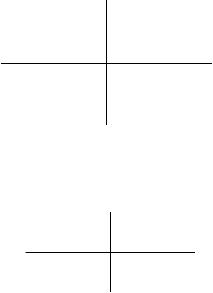
Рис 14.10
Крім кінцевих переміщень на стержневий скінченний елемент можуть діяти рівномірно роз поділені навантаження які орієнтуються за осями або локальної рис 14.10,а або глобальної рис 14.10,б системи координат Зв’язок між цими двома системами навантажень встановлюється співвідношеннями
q |
x |
qxly |
|
cos |
qylx |
sin |
; |
||||
|
|
|
l |
|
|
|
|
l |
|
(14.10) |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
qy |
qxly sin |
qylx cos |
|||||||||
|
|
|
|
l |
|
|
|
l |
|
|
|
або навпаки |
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
q |
l |
|
cos |
|
qyl |
sin |
; |
|
x |
x |
|
|
|
||||||
|
|
|
ly |
|
|
|
|
ly |
|
|
|
|
|
|
|
|
|
|
|
|
(14.11) |
||
|
|
|
|
q |
l |
|
|
qyly |
|
||
|
q |
|
|
sin |
|
cos . |
|||||
|
y |
x |
|
|
|
||||||
|
|
|
lx |
|
|
|
|
lx |
|
|
|
|
|
|
|
|
|
|
|
|
|
||

11
Так само за локальними рис 14.11,а або за глобальними координатними осями рис 14.11,б) орієнтуються вантажні реакції які зумовлюються розподіленими вздовж стержня навантаження ми
Рис 14.11
Нумерація вантажних реакцій також суворо визначена Вантажні реакції в локальній і в глобальній системі координат також можуть бути представле
ні у вигляді векторів
|
p1 |
p 2 |
p 3 |
p 4 |
p 5 |
|
T |
|
|
pe |
p |
6 e |
, |
||||||
|
|
p1 |
p2 |
p3 |
p4 |
p5 |
|
T |
|
pe |
p6 e . |
|
|||||||
Для стержня що має на кінцях шарніри
|
|
p1 |
p 2 |
p 3 |
|
T |
pe |
|
p |
4 e |
|||
|
|
p1 |
p2 |
p3 |
|
T |
pe |
|
p4 e |
||||
ілком очевидно що в разі відсутності розподілених навантажень ці вектори є нульовими При наявності розподілених навантажень значення елементів векторів вантажних реакцій зале жать від граничних умов по кінцям стержня Так для скінченного елементу першого типу рис 14.3,а тобто для елемента що має жорсткі вузли на обох кінцях
|
|
|
|
|
q |
x |
l |
|
|
|
qxly |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||
|
|
|
|
|
2 |
|
|
|
|
|
|
||
|
p1 |
|
|
qyl |
|
p1 |
|
qylx |
|
|
|||
|
|
2 |
|
|
2 |
|
|
||||||
|
p 2 |
|
|
q |
l2 |
|
p2 |
|
q l2 |
|
|
||
|
|
|
|
|
|
y |
|
|
|
|
y y |
|
(14.12) |
p 3 |
|
12 |
p3 |
12 |
. |
||||||||
pe |
p 4 |
|
|
qxl |
; pe |
p4 |
|
qxly |
|
||||
|
|
|
|
|
|
|
|||||||
|
p 5 |
|
2 |
|
|
p5 |
2 |
|
|
||||
|
p |
|
|
|
qyl |
|
p |
|
qylx |
|
|
||
|
|
6 |
e |
2 |
|
|
6 |
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
qyl2 |
|
|
|
qyly2 |
|
|
||
|
|
|
|
12 e |
|
|
12 |
e |
|
||||
12
Матриці жорсткості і вектори вантажних реакцій для скінченних елементів інших типів наве дено в Додатках 3.
Між кінцевими характеристиками в глобальній та в локальній системах координат може бути встановлений формальний зв’язок
|
|
e |
Te |
e , |
|
|
|
(14.13) |
|
|
re |
Tere , |
|
|
|
(14.14) |
|
|
|
pe Tepe |
, |
|
|
(14.15) |
||
де |
|
|
|
|
|
|
|
|
|
cos |
sin |
0 |
0 |
0 |
0 |
|
|
|
sin |
cos |
0 |
0 |
0 |
0 |
|
|
T |
0 |
|
0 |
1 |
0 |
0 |
0 . |
|
e |
0 |
|
0 |
0 |
cos |
sin |
0 |
|
|
|
|
||||||
|
0 |
|
0 |
0 |
sin |
cos |
0 |
|
|
0 |
|
0 |
0 |
0 |
0 |
1 |
e |
Квадратна матриця Te називається матрицею перетворення стержневого елемента e.
Для стержня с шарнірами на кінцях матриця перетворення набуває вигляду
|
cos |
sin |
0 |
0 |
T |
sin |
cos |
0 |
0 |
e |
0 |
0 |
cos |
sin |
|
||||
|
0 |
0 |
sin |
cos |
Матриці жорсткості стержневих скінченних елементів
Між кінцевими реакціями і кінцевими переміщеннями існує зв’язок який у глобальній систе мі координат може бути записаний у формі
re ke e , |
(14.16) |
де ke – матриця жорсткості елемента e в глобальній системі координат Для стержневого скінче ного елемента першого типу матриця має вигляд

|
|
|
|
|
|
|
13 |
|
k11 |
k12 |
k13 |
k14 |
k15 |
k16 |
|
|
k21 |
k22 |
k23 |
k24 |
k25 |
k26 |
|
ke |
k |
k |
k |
k |
k |
k |
|
k31 |
k32 |
k33 |
k34 |
k35 |
k36 |
(14.17) |
|
|
41 |
42 |
43 |
44 |
45 |
46 |
|
|
k51 |
k52 |
k53 |
k54 |
k55 |
k56 |
|
|
k61 |
k62 |
k63 |
k64 |
k65 |
k66 |
e |
Елементи матриці жорсткості – це реакції на кінцях тобто кінцеві реакції стержневого скін ченного елемента які зумовлюються його кінцевими переміщеннями Перший індекс характери зує номер кінцевої реакції а другий – номер кінцевого переміщення яке цю реакцію викликало Наприклад елемент k25 – це кінцева реакція r2 див рис 14.9,б від дії примусового переміщення
5 1 див рис 14.9,а за умови що всі інші кінцеві переміщення дорівнюють нулю Величини ре акцій залежать від типу скінченного елемента Так для скінченного стержневого елемента що має
жорсткі вузли з обох сторін рис 14.3,а |
|
елементи матриці жорсткості мають значення |
|
||||||||||||||||||||||||||||||||
k |
|
k |
|
k |
|
k |
|
|
f cos2 |
|
|
|
12i sin2 |
; |
|
|
|
|
|
|
|
|
|
|
|||||||||||
11 |
|
44 |
|
14 |
|
|
|
|
41 |
|
|
|
|
|
|
|
l2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
k |
22 |
k |
55 |
k |
25 |
k |
52 |
f sin2 |
|
|
|
12i cos2 |
; |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
k33 k66 |
4i; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12i |
|
|
|
|
(14.18) |
|
k12 k21 |
k45 |
k54 |
k15 k51 |
k24 |
k42 |
|
|
f l2 |
|
sin |
cos |
|
; |
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||
k |
|
k |
31 |
k |
|
k |
61 |
k |
46 |
k |
64 |
k |
34 |
k |
43 |
|
6i sin ; |
|
|
|
|
|
|
||||||||||||
13 |
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
35 |
k |
53 |
k |
56 |
k |
65 |
k |
23 |
k |
32 |
k |
26 |
k |
62 |
6i cos |
; |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k36 k63 2i. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Тут позначено |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
EI ; |
|
f |
EA |
, |
|
(14.19) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
l |
|
|
|
де l – довжина EI – жорсткість стержня на згин, EA – жорсткість стержня на поздовжні деформа ції

14
Для стержневого скінченого елементу четвертого типу шарнірне приєднання з обох сторін матриця жорсткості в глобальній системі координат набуває вигляду
|
|
k11 |
k12 |
k13 |
k14 |
|
|
|
|
|
ke |
k21 |
k22 |
k23 |
k24 |
|
|
|
|
|
|
|
|
k31 |
k32 |
k33 |
k34 |
|
|
|
|
|
|
|
k41 |
k42 |
k43 |
k44 |
e |
|
|
|
(14.20) |
|
f |
cos2 |
|
f sin |
|
f sin2 |
f sin |
|||
|
|
cos |
cos |
|||||||
|
f |
sin |
cos |
f sin2 |
|
f sin |
cos |
f sin2 |
||
f sin |
2 |
f sin |
cos |
f cos2 |
|
f sin |
cos |
|||
|
|
|||||||||
|
f sin |
cos |
f sin |
2 |
f sin |
cos |
f sin2 |
e |
||
|
|
|
|
|
|
|
|
|
|
|
изначення зусиль у стержнях |
|
|
|
|
|
|
|
|||
Розв’язок рівняння рівноваги |
14. |
визначає вектор вузлових переміщень |
||||||||
|
|
|
|
|
K 1F . |
|
|
|
(14.21) |
|
Таким чином стають відомими переміщення всіх вузлів дискретної моделі Внаслідок нероз ривності деформацій кінці стержнів які приєднуються до вузлів матимуть такі ж самі переміщення що й вузли Отже для кожного стержня дискретної моделі можна побудувати вектор кін цевих переміщень у глобальній системі координат
|
|
|
|
|
1 |
|
xi |
|
|
|
|
|
|
|
2 |
|
yi |
|
|
{ |
}T |
3 |
|
i |
. |
(14.22) |
|||
e |
|
i |
j |
e |
4 |
|
xj |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
5 |
|
yj |
|
|
|
|
|
|
|
6 |
e |
j |
e |
|
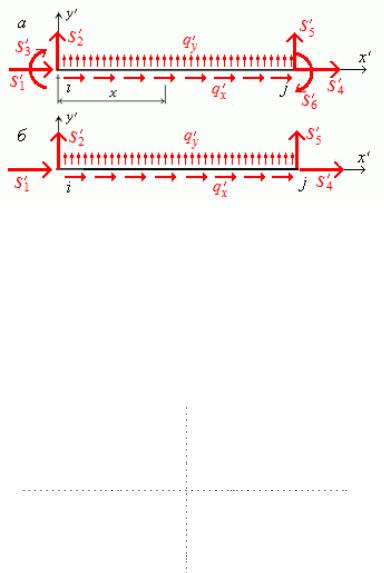
Сумарні кінцеві реакції стержня в локальній системі координат рис 14.12,а)
se {si |
sj }Te {s1 s 2 s 3 s 4 s 5 s 6}Te . |
складаються з кінцевих реакцій ri |
що зумовлені переміщеннями вузлів дискретної моделі 14.22), |
і кінцевими силами pi які викликано дією розподіленого на стержні зовнішнього навантаження
se re pe . |
(14.23) |
15
Рис
Сумарні кінцеві реакції можуть бути обчислені за формулою
se he e pe . (14.24)
Вигляд матриці he залежить від граничних умов на кінцях стержня Так для стержня що має на обох кінцях жорсткі вузли
|
|
|
|
fC |
|
|
|
fS |
|
0 |
|
|
fC |
|
fS |
0 |
|
|
|||||||||||||||||||
|
|
|
12i |
S |
|
12i |
C |
|
6i |
|
12i |
|
S |
|
12i |
C |
|
6i |
|
||||||||||||||||||
|
|
|
|
l2 |
|
l2 |
|
|
|
l |
|
l2 |
|
|
|
|
l2 |
|
|
l |
|
||||||||||||||||
|
|
|
6i |
|
S |
|
6i |
|
C |
|
4i |
|
6i |
|
S |
|
|
6i |
|
C |
|
2i |
|
||||||||||||||
he |
|
|
|
l |
l |
l |
|
|
|
l |
(14.25), |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
||||||||||||||||
|
|
fC |
|
fS |
|
|
|
|
fC |
|
|
|
|
fS |
|
|
|||||||||||||||||||||
|
12i |
S |
|
12i |
C |
|
6i |
|
12i |
S |
12i |
C |
|
6i |
|
||||||||||||||||||||||
|
|
|
l2 |
|
|
l |
|
|
|
|
l2 |
|
l |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
l2 |
|
|
|
|
|
l2 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
6i |
|
S |
|
6i |
|
C |
|
2i |
|
6i |
|
S |
|
|
6i |
|
C |
|
4i |
|
||||||||||||||
|
|
|
|
l |
l |
|
l |
|
|
|
l |
|
e |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
а для стержня з шарнірами на кінцях |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
fC |
fS |
fC |
|
fS |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
he |
0 |
0 |
|
0 |
|
|
|
|
|
0 . |
|
|
|
|
|
|
(14.26) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
fC |
fS |
fC |
|
fS |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||
Тут позначено S sin , |
C cos . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Нумерація сумарних кінцевих реакцій для стержня |
що має на кінцях шарнірні вузли предста |
||||||||||||||||||||||||||||||||||||
влена на рис 14.12,б. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приклавши сумарні кінцеві реакції до стержня рис 14. |
|
можемо обчислити внутрішні зу |
|||||||||||||||||||||||||||||||||||
силля в будь-якому його перерізі розглядаючи рівновагу однієї з його частин Наприклад у перері зі з абсцисою x рис 14.12,а маємо

16
|
|
M x M x s |
2 x s 3 q y x |
2 |
; |
|
|
|
л в. |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
л в. |
|
|
|
|
|
|
Qx y s 2 |
q y x; |
|
|
(14.27) |
|
|
л в. |
|
|
|
|
|
|
Nx x s1 q x x. |
|
|
|
|
14.2. риклад розрахунку плоскої рами |
|
|
|
|
||
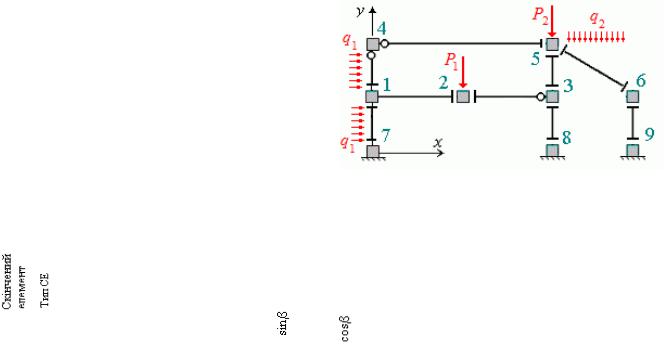
Необхідно виконати статичний розрахунок плоскої рами |
рис 14. |
На раму діють зосере |
||||
джені сили |
P1 10кН |
і P2 20кН а також рівномірно розподілені навантаження з інтенсивністю |
||||
q1 2,4кН м |
і q2 3,0кН м. |
|
|
|
|
|
Рис 14.13
Стояки мають жорсткості на згинальні та поздовжні деформації відповідно EI 1, EA 100 а
ригелі – вдвічі більшу EI 2, EA 200 .
ерехід до дискретної скінченно-елементної моделі
Для переходу від заданої розрахункової схеми до дискретної скінченно-елементної моделі розіб’ємо схему на окремі стержневі елементи які поєднуються у вузлах За вузли приймаємо точ ки сполучення окремих стержнів опорні точи а також точку прикладення зовнішньої зосередже ної сили P1 Пронумеруємо вузли в довільному порядку Початок глобальної системи візьмемо у вузлі Дискретна модель наведена на рис 14.14.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
||
|
ізико-геометричні |
характеристики |
|
|
|
|
|
|
|
|
||||||||||
скінченних елементів |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Для кожного стержня дискретної моделі |
|
|
|
|
|
|
|
|
||||||||||||
необхідно обчислити довжину l |
нахил осей |
|
|
|
|
|
|
|
|
|||||||||||
локальної системи координат |
, cos ), по |
|
|
|
|
|
|
|
|
|||||||||||
гонні жорсткості |
i,f |
а також визначити тип |
|
|
|
|
|
|
|
|
||||||||||
його граничних |
умов рис 14. |
Результати |
|
|
Рис 14.14 |
|
|
|
|
|||||||||||
обчислень занесені до табл 14.1. |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблиця 14.1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Початок |
|
Кінець |
|
l |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
СЕ |
|
|
СЕ |
|
|
|
|
|
|
EI |
EA |
|
i |
|
f |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
|
yi |
|
xj |
|
y j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1-2 |
1 |
0 |
|
3 |
|
4 |
|
3 |
|
4 |
0 |
|
1 |
2 |
200 |
|
0,5 |
|
50 |
|
2-3 |
2 |
4 |
|
3 |
|
8 |
|
3 |
|
4 |
0 |
|
1 |
2 |
200 |
|
0,5 |
|
50 |
|
4-5 |
3 |
0 |
|
6 |
|
8 |
|
6 |
|
8 |
0 |
|
1 |
2 |
200 |
|
0,25 |
|
25 |
|
5-6 |
1 |
8 |
|
6 |
|
12 |
|
3 |
|
5 |
-0,6 |
|
0,8 |
2 |
200 |
|
0,4 |
|
40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1-7 |
1 |
0 |
|
3 |
|
0 |
|
0 |
|
3 |
-1 |
|
0 |
1 |
100 |
|
0,333 |
|
33,33 |
|
1-4 |
2 |
0 |
|
3 |
|
0 |
|
6 |
|
3 |
1 |
|
0 |
1 |
100 |
|
0,333 |
|
33,33 |
|
3-8 |
1 |
8 |
|
3 |
|
8 |
|
0 |
|
3 |
-1 |
|
0 |
1 |
100 |
|
0,333 |
|
33,33 |
|
3-5 |
1 |
8 |
|
3 |
|
8 |
|
6 |
|
3 |
1 |
|
0 |
1 |
100 |
|
0,333 |
|
33,33 |
|
6-9 |
1 |
12 |
|
3 |
|
12 |
|
0 |
|
3 |
-1 |
|
0 |
1 |
100 |
|
0,333 |
|
33,33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Усі жорсткі вузли дискретної моделі мають три ступені вільності Вузол |
до якого всі елеме |
|||||||||||||||||||
нти примикають шарнірно |
має два ступеня вільності |
Схема можливих вузлових переміщень на |
||||||||||||||||||
ведена на рис 14.15. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||

18
|
|
|
|
|
Рис |
|
|
|
|
|
Вектор вузлових переміщень має |
компонентів |
|
|
|
|
|
||||
|
1 |
2 |
3 |
4 |
5 |
6 |
24 |
25 |
T . |
|
|
26 |
|
||||||||
Переміщення опорних вузлів дорівнюють нулю |
|
|
|
|
|
|||||
18 |
|
19 20 |
|
21 |
22 |
23 |
24 |
25 |
26 0 . |
|
Виключивши нульові компоненти з вектора вузлових переміщень маємо остаточно |
|
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
15 |
16 |
T . |
|
|
17 |
|
||||||||
Таким чином дискретна модель має |
|
невідомих вузлових переміщень і отже |
ступенів ві |
|||||||
льності
обудова вектора вузлових навантажень
Вектор вузлових навантажень має компоненти які відповідають компонентам вектора вузло вих переміщень
F F1 F2 F3 F4 F5 F6 |
F15 F16 F17 |
T . |
Схема дії зовнішніх вузлових навантажень наведена рис 14.16.
Згідно до формули 14. вектор вузлових навантажень складається з двох векторів Перший з них – це вектор зовнішніх зосереджених сил і моментів що безпосередньо діють на вузли
F {F1 F2 F3  F4 F5 F6
F4 F5 F6  F7 F8 F9
F7 F8 F9  F10 F11
F10 F11  F12 F13 F14
F12 F13 F14  F15 F16 F17}T .
F15 F16 F17}T .

19
Рис 14.16
Порівнюючи схему завантаження дискретної моделі рис 14. зі схемою компонентів вузло
вих навантажень |
рис 14. |
можна записати |
|
|
|
|
|
|
|
F5 10; |
F13 20. |
|
|
Усі інші компоненти дорівнюватимуть нулю |
тому |
|
|
|||
|
F {0 0 0 |
0 10 0 0 0 |
0 0 0 0 20 0 0 0 0}T . |
|
||
Вектор Q реактивних сил |
що передаються на вузли від розподілених на стержні наванта |
|||||
жень також має |
компонентів |
|
|
|
|
|
Q {Q1 Q2 |
Q3 Q4 Q5 |
Q6 Q7 Q8 Q9 |
Q10 Q11 Q12 Q13 Q14 |
Q15 Q16 |
Q17}T . |
|
Схема дії компонентів цього вектора аналогічна компонентам вектора F |
рис 14. |
Для обчи |
||||
слення компонентів вектора Q розглянемо завантажені стержні окремо |
|
|
||||
Рис 14.17
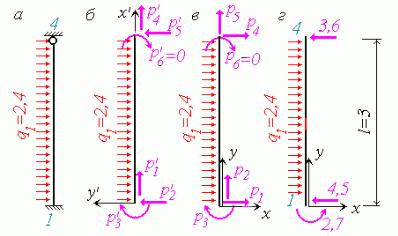
Стержень -7 рис 14.18,а Скінченний елемент має з обох боків жорсткі вузли і відноситься до першого типу Навантаження в локальній системі координат рис 14.18,б):
qx 0; |
q y 2,4. |

20
Рис 14.18
Вантажні реакції в локальній системі координат
p |
qxl |
|
0; |
|
|
|
|
p |
4 |
|
qxl |
|
0; |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||
p2 |
|
|
q yl |
|
|
2,4 3 |
3,6; |
p |
5 |
|
|
|
q yl |
|
2,4 3 |
|
3,6; |
||||||||
2 |
|
2 |
|
|
|
2 |
|
|
2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
q yl2 |
|
2,4 32 |
|
|
|
|
|
|
|
q yl |
2 |
|
|
2,4 32 |
|||||||||
p3 |
|
|
|
|
|
|
|
|
1,8; |
p |
6 |
|
|
|
|
|
|
|
|
|
1,8. |
||||
12 |
|
|
12 |
|
12 |
|
12 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Вантажні реакції у глобальній системі координат можна визначити по формулам 14. або шляхом порівняння реакцій у локальній та глобальній системах координат Так з порівняння ван тажних реакцій в локальній рис 14.18,б і в глобальній рис 14.18,в системах координат доходи мо висновку
p1 p2 3,6; |
p4 |
p5 3,6; |
p2 p1 0; |
p5 p4 0; |
|
p3 p3 1,8; |
p6 |
p6 1,8. |
Вантажні реакції орієнтовані по осях глобальної системи координат з урахуванням знаків по казано на рис 14.18,г:
Стержень -4 рис 14.19,а Скінченний елемент має жорсткий вузол на початку і шарнірний на кінці і тому відноситься до другого типу Навантаження в локальній системі координат
qx 0; |
q y 2,4. |
21
|
|
|
|
|
|
|
|
|
|
|
|
Рис 14.19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Вантажні реакції в локальній системі координат рис |
|
|
|
б): |
|
|
|||||||||||||||||||||
p |
qxl |
0; |
|
|
|
|
p |
4 |
|
qxl |
|
0; |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,4 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
p2 |
|
5q yl |
|
5 |
4,5; |
p5 |
|
|
q yl |
|
2,4 |
3 |
|
3,6; |
|||||||||||||
8 |
|
|
|
8 |
|
|
|
2 |
|
|
2 |
|
|
||||||||||||||
|
|
q yl2 |
|
|
|
2,4 32 |
|
|
|
|
|
|
|
q yl |
2 |
|
|
2,4 |
32 |
||||||||
p |
|
|
|
|
|
|
|
|
2,7; |
p |
6 |
|
|
|
|
|
|
|
|
|
|
1,8. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
3 |
|
|
|
8 |
|
|
|
|
8 |
|
|
|
|
|
|
|
12 |
|
|
|
12 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Порівнючи вантажні реакції орієнтовані по осях локальної системи координат стержня рис 14.19,б з вантажними реакціями спрямованими по осях глобальної системі координат скін ченно-елементної моделі рис 14.19,в можемо записати
p1 p2 4,5; |
p4 |
p5 3,6; |
p2 p1 0; |
p5 p4 0; |
|
p3 p3 2,7; |
p6 |
0. |
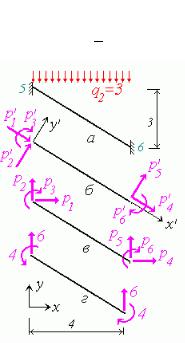
Вантажні реакції у глобальній системі координат з урахуванням знаків показано на рис 14.19,г. Стержень -6 рис 14.20,а). Скінченний елемент має з обох боків жорсткі вузли і відноситься
до першого типу Навантаження в глобальній системі координат
qx 0; |
qy 3. |
Для зручності обчислення вантажних реакцій орієнтованих за локальною системою коорди нат перетворимо розподілене навантаження до локальної системи координат за формулами
(14.10):
22
q |
1l qxly cos |
qylx sin |
15 0 3 4 0,6 1,44; |
|||||
q y |
|
1 |
qxly sin |
qylx cos |
|
1 |
0 |
3 4 0,8 1,92. |
|
|
l |
|
|
|
5 |
|
|
Рис 14.20
Вантажні реакції за локальною системою координат рис 14.20,б):
p |
qxl |
|
|
1,44 5 |
3,60; |
p |
4 |
|
qxl |
|
3,60; |
||||||||||
|
|
|
|
||||||||||||||||||
1 |
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
||
p2 |
|
|
q yl |
|
1,92 5 |
4,80; |
p |
5 |
|
|
|
q yl |
4,80; |
||||||||
2 |
|
2 |
|
|
|
|
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
p3 |
|
q yl2 |
|
1,92 |
52 |
4,00; |
p |
6 |
|
|
q yl |
2 |
4,00. |
||||||||
12 |
|
|
|
12 |
|
|
12 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
За глобальною системою координат рис 14.20,в):
p |
qxly |
|
|
0; |
|
|
|
|
|
|
p |
4 |
0; |
||||||
|
|
|
|
|
|
|
|
||||||||||||
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
3 4 |
|
|
|
|
|
|||||
p |
2 |
|
|
qylx |
|
|
6,00; |
p |
5 |
6,00; |
|||||||||
2 |
|
|
|
2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
qylx2 |
|
|
|
|
qxly2 |
3 42 |
|
|
|
|
||||||
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 4,00; |
p |
6 |
4,00. |
||
|
|
|
|
|
|
|
|
|
|
||||||||||
3 |
|
12 |
|
|
|
12 |
|
|
|
12 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
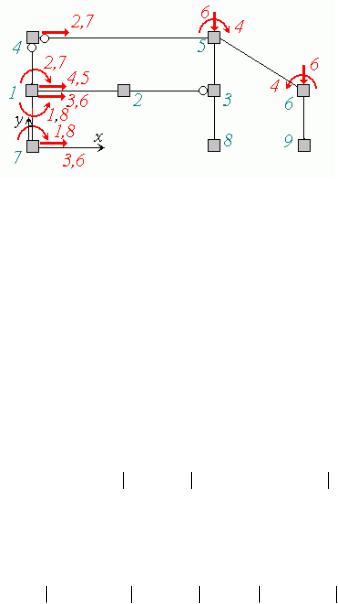
Вантажні реакції у глобальній системі координат з урахуванням знаків показано на рис 14.20,г: Прикладаємо вантажні реакції завантажених стержнів до вузлів дискретної моделі змінивши
напрямки на протилежні рис 14.21).
23
Рис 14.21
Порівнюючи сили на рис 14. і на рис 14. можемо записати
Q1 3,6 4,5 8,1;
Q3 2,7 1,8 0,9;
Q10 2,7;
Q13 6;
Q14 4;
Q16 6;
Q17 4.
Усі інші елементи вектора Q дорівнюють нулю Таким чином
Q 8,1 |
0 |
0,9 |
0 |
0 |
0 |
0 |
0 |
0 |
2,7 0 0 6 4 0 |
6 |
4 T . |
||
Додаючи вектори F і Q одержуємо згідно з формулою |
14. |
вектор вузлових навантажень |
|||||||||||
дискретної моделі |
|
|
|
|
|
|
|
|
|
|
|
|
|
F 8,1 |
0 |
0,9 |
0 |
10 |
0 |
0 |
0 |
0 |
2,7 0 |
0 |
6 4 0 |
6 |
4 T . |
Матриця жорсткості дискретної моделі |
|
|
|
|
|
|
|
||||||
Дискретна модель рами що розраховується має |
ступенів вільності Тому матриця жорстко |
||||||||||||
сті дискретної моделі є квадратною матрицею17x17: |
|
|
|
|
|
||||||||
|
|
|
|
|
K1,1 |
|
K1,2 |
|
K1,17 |
|
|
|
|
|
|
|
K |
K2,1 |
|
K2,2 |
|
K2,17 . |
|
|
|
||
|
|
|
|
|
K17,1 |
K17,2 |
|
K17,17 |
|
|
|
|
|
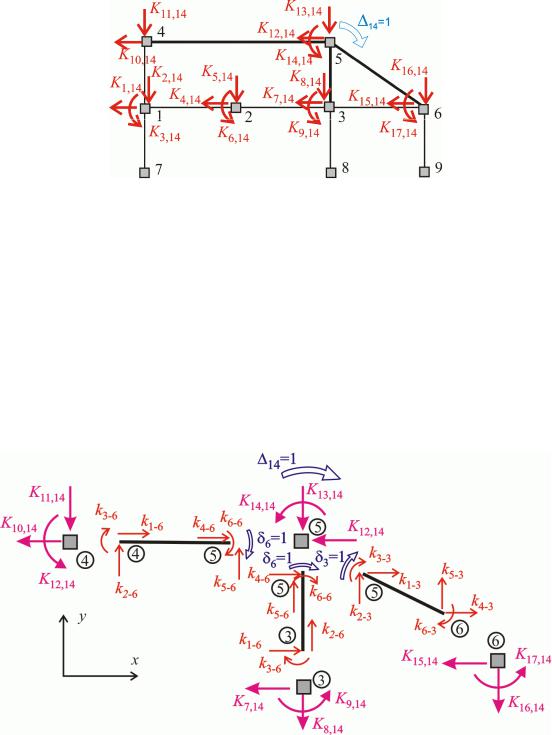
Елементи матриці – це величини вузлових реакцій що зумовлюються одиничними вузловими переміщеннями Для обчислення коефіцієнтів матриці жорсткості необхідно почергово надавати одиничні переміщення вузлам дискретної моделі і знаходити сили які при цьому передаватимуться на вузли
|
24 |
Обчислимо наприклад елементи |
стовпця матриці жорсткості З цією метою надамо дис |
кретній моделі примусове вузлове переміщення 14 1 вважаючи що всі інші переміщення вузлів дорівнюють нулю Тобто надамо вузлу примусовий одиничний поворот вважаючи що всі інші вузли не переміщуються На вузли дискретної моделі з боку стержнів передаватимуться кінцеві реакції зумовлені деформаціями стержнів рис 14.22).
Рис 14.22
Унаслідок переміщення вузла деформуються стержні -5, 5-6, 3- які до нього приєднують ся Вони виділені на рисунку товстими лініями Тільки в цих стержнях виникають напруження і кінцеві реакції що передаються на вузли дискретної моделі і зумовлюють появу вузлових реак цій Тому можна відразу зазначити якщо до вузла приєднуються тільки недеформовані стержні то
вузлових |
реакцій в |
даному вузлі не |
виникає На |
цій підставі |
можна вважати що |
|
K1,14 K2,14 |
K3,14 K4,14 |
K5,14 K6,14 |
0 Для обчислення реакцій які діють на вузли з боку де |
|||
формованих стержнів |
розглянемо |
окремо |
відповідний |
фрагмент у |
збільшеному масштабі |
|
рис 14.23). |
|
|
|
|
|
|
Рис 14.23

|
|
|
|
|
|
|
25 |
Разом із поворотом |
14 1 вузла |
повертаються кінці стержнів |
-5, 3- і |
- |
Але якщо для |
||
стержня - це поворот його початку і тому на схемі він позначений |
3 1 то для стержнів |
- і - |
|||||
5 – це повороти кінців |
тобто 6 1 |
Тому на стержні - кінцеві реакції другим мають індекс |
|||||
( k1,3 , k2,3 , k3,3 , k4,3 , k5,3 , |
k6,3 а на стержнях - і -5 – індекс |
k16 , |
k26 , k36 , |
k46 , |
k56 , k66 |
Вели |
|
чини кінцевих реакцій визначаються матрицями жорсткості скінченних елементів відповідних ти пів Так стержні - і - є елементами першого а стержень -5 – елементом другого типу Дані для обчислень вибираємо з табл 14.4.
|
|
|
|
|
|
|
3 5 |
|
|
|
|
|
|
|
|
|
K |
7,14 |
k |
3 5 |
|
6i sin |
6 0,333 1 0,666; |
|
|
|
|||||||
|
16 |
|
|
l |
|
|
|
3 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
6i cos |
3 5 |
|
|
|
|
|
|
|
||
K |
8,14 |
k |
3 5 |
|
|
0; |
|
|
|
|
|
|
||||
|
|
26 |
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K9,14 |
k363 5 |
2i 3 5 2 0,333 0,666; |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
4 5 |
|
|
|
|
|
|
|
|
|
K |
10,14 |
k |
4 5 |
|
3i sin |
|
0; |
|
|
|
|
|
|
|||
|
16 |
|
|
l |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3i cos |
4 5 |
|
3 0,25 1 0,09375; |
|
|
|||||
K |
11,14 |
k |
4 5 |
|
|
|
|
|
||||||||
|
|
26 |
|
|
|
l |
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
4 5 |
6i sin |
5 6 |
6i sin |
3 5 |
|
K |
12,14 |
k |
4 5 |
k5 6 |
k3 5 |
|
3i sin |
|
|
|
||||||
|
|
46 |
|
|
13 |
46 |
|
|
l |
|
|
l |
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
0 |
6 0,4 |
0,6 |
|
|
6 |
0,333 |
1 |
0 0,288 0,666 0,954; |
||||||
|
|
|
5 |
|
|
3 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 5 |
|
6i cos |
5 6 |
6i cos |
3 5 |
K |
13,14 |
k |
4 5 |
k5 6 |
k3 5 |
|
3i cos |
|
|
|
||||||
|
56 |
|
|
23 |
56 |
|
l |
|
|
|
l |
|
l |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
3 0,25 1 6 0,4 0,8 0 0,09375 0,384 0) 0,29025; |
|
|||||||||||||
|
|
|
8 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
K14,14 |
k664 5 |
k335 6 |
k663 5 |
3i 4 5 |
4i 5 6 4i 3 5 |
|
|
|
||||||||
|
|
3 0,25 4 0,4 4 0,333 3,682; |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
5 6 |
|
|
|
|
|
|
|
|
K15,14 |
k435 6 |
|
6i sin |
|
6 0,4 |
0,6 0,288; |
|
|
||||||||
|
|
|
|
|
|
|
l |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
6i cos |
5 6 |
6 0,4 0,8 0,384; |
|
|
|
|||||
K |
16,14 |
k |
5 6 |
|
|
|
|
|
||||||||
|
53 |
|
|
l |
|
|
|
5 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
K17,14 |
k635 6 |
2i 5 6 2 0,4 0,8. |
|
|
|
|
|
|||||||||
Система рівнянь рівноваги вузлів
Матричне рівняння рівноваги вузлів 14. еквівалентне системі рівнянь

26
K1,1 |
1 |
|
K1,2 |
2 |
|
|
K1,17 |
17 |
F1 |
|
0; |
K2,1 |
1 |
|
K2,2 |
2 |
|
|
K2,17 |
17 |
F2 |
|
0; |
|
|
|
|
|
|
|
|
|
|
|
|
K17,1 |
1 |
|
K17,2 |
2 |
|
|
K17,17 |
17 |
F17 |
|
0. |
У результаті розв’язання системи рівнянь маємо такі значення вузлових переміщень дискрет
ної моделі |
|
|
|
|
|
|
|
|
Вузол |
: |
1 13,228; |
2 -0,1827; |
3 |
7,9986; |
|||
Вузол |
: |
4 |
13,131; |
5 |
-35,666; |
6 |
1,5684; |
|
Вузол |
: |
7 |
13,034; |
8 |
-0,6678; |
9 |
1,6059; |
|
Вузол |
: |
10 |
12,923; |
11 -0,1815; |
|
|
||
Вузол |
: |
12 |
12,707; |
13 -1,2679; |
14 0,5571; |
|||
Вузол |
: |
15 |
13,063; |
16 -0,4094; |
17 0,4117. |
|||
Обчислення внутрішніх зусиль
Визначення вузлових переміщень дискретної моделі дає змогу обчислити сумарні кінцеві реа кції в кожному скінченному елементі Обчислимо наприклад сумарні кінцеві реакції в стержні -
рис 14.14).
Побудуємо вектор кінцевих переміщень у глобальній системі координат для стержня -6:
|
|
1 |
|
|
12 |
|
12,707 |
|
|
|
|
|
|
||
|
|
2 |
|
|
13 |
|
1,2679 |
5 6 |
3 |
|
|
14 |
|
0,5571 . |
|
|
|
4 |
|
|
15 |
|
13,063 |
|
|
5 |
|
|
16 |
|
0,4094 |
|
|
6 |
5 6 |
17 |
|
0,4117 |
|
|
|
|
|
||||
Скомпонуємо вектор вантажних реакцій стержня |
- у локальній системі координат |
||||||
|
|
|
|
p1 |
|
3,60 |
|
|
|
|
|
p 2 |
|
|
4,80 |
|
|
|
|
p 3 |
|
4,00 |
|
|
|
p5 6 |
|
p 4 |
|
3,60 . |
|
|
|
|
|
p 5 |
|
|
4,80 |
|
|
|
|
p 6 |
5 6 |
|
4,00 |

27
Складемо матрицю h5 6 на підставі співвідношень 14. як для стержня з першим типом граничних умов При обчисленнях дані вибираємо з таблиці фізико-геометричних характеристик
скінченних елементів |
Табл 14. В результаті маємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
32 |
|
24 |
|
0 |
|
|
|
32 |
|
24 |
|
0 |
|
|
|
||
|
|
|
0,1152 |
0,1536 |
0,48 |
0,1152 |
0,1536 |
0,48 |
|
|
||||||||||||
|
|
h5 6 |
|
0,288 |
0,384 |
|
1,6 |
|
|
0,288 |
|
0,384 |
|
0,8 |
. |
|
||||||
|
|
|
|
32 |
|
24 |
|
0 |
|
|
|
32 |
|
24 |
|
0 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
0,1152 |
0,1536 |
0,48 |
|
|
0,1152 |
0,1536 |
0,48 |
|
|
||||||||||
|
|
|
|
0,288 |
0,384 |
|
0,8 |
|
|
0,288 |
|
0,384 |
|
1,6 |
|
|
|
|||||
Виконуємо обчислення за формулою 14.24): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
s1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s 3 |
h5 6 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
s5 6 |
s 4 |
5 6 p5 6 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s 6 |
5 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
24 |
0 |
|
32 |
|
24 |
|
0 |
|
|
12,707 |
|
3,60 |
|
|
5,615 |
|||||
|
0,1152 |
0,1536 |
0,48 |
0,1152 |
0,1536 |
0,48 |
|
|
1,2679 |
|
|
4,80 |
|
|
4,162 |
|||||||
|
0,288 |
0,384 |
1,6 |
0,288 |
0,384 |
0,8 |
|
0,5571 |
|
4,00 |
|
2,347 |
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
32 |
24 |
0 |
|
32 |
24 |
|
0 |
|
|
|
13,063 |
|
3,60 |
|
|
12,815 |
|||||
|
0,1152 |
0,1536 |
0,48 |
0,1152 |
0,1536 |
0,48 |
|
0,4094 |
|
|
4,80 |
|
|
5,438 |
||||||||
|
0,288 |
0,384 |
0,8 |
0,288 |
0,384 |
1,6 |
|
|
0,4117 |
|
|
4,00 |
|
|
5,536 |
|||||||
Знайдені сумарні кінцеві реакції прикладаються до скінченного елемента рис 14.24).
Рис 14.24

28
Обчислимо внутрішні зусилля у довільному перерізі стержня
M x |
M x |
4,162 x 2,347 |
|
3 x2 |
; |
|
|
|
л в |
|
|
2 |
|
Qx |
y 4,162 3 x cos ; |
|
|
|
||
|
|
л в |
|
|
|
|
Nx |
x 5,165 3 x sin . |
|
|
|||
|
|
л в |
|
|
|
|
Зауважимо що sin sin , cos |
cos . |
|
|
|
||
Таким чином на початку стержня |
x x 0 ) |
|
|
|
||
Mп 2,347; |
Qп 4,162; Nп |
5,165. |
||||
В середині стержня x 2,5; x 2 )
Mc 4,162 2,5 2,347 3 22 2,058; 2
Qc 4,162 3 2 0,8 0,638; Nc 5,165 3 2 0,6 8,765.
На кінці стержня x 5; x 4 )
M к 5, 536; |
Qк 5, 438; |
Nк 12,815. |
Аналогічні обчислення виконуються для всіх інших стержнів Результати розрахунків запи шемо до табл 14.2.
Таблиця 14.2
СЕ |
Mп |
Mс |
Mк |
Qп |
Qк |
Nп |
Nк |
|
|
|
|
|
|
|
|
|
|
1- |
2 |
-9.047 |
3.215 |
15.477 |
6.131 |
6.131 |
-4.853 |
-4.853 |
2- |
3 |
15.477 |
7.738 |
0.000 |
-3.869 |
-3.869 |
-4.853 |
-4.853 |
3- |
6 |
3.817 |
0.597 |
-2.623 |
-1.610 |
-1.610 |
1.456 |
1.456 |
4- |
5 |
0.000 |
-0.158 |
-0.316 |
-0.039 |
-0.039 |
-5.400 |
-5.400 |
5- |
6 |
-2.347 |
2.058 |
-5.536 |
4.162 |
-5.438 |
-5.613 |
-14.813 |
1- |
7 |
3.646 |
1.766 |
5.286 |
-3.053 |
4.147 |
-6.091 |
-6.091 |
1- |
4 |
5.400 |
5.400 |
0.000 |
1.800 |
-5.400 |
0.039 |
0.039 |
3- |
5 |
2.731 |
0.350 |
-2.031 |
-1.587 |
-1.587 |
-20.002 |
-20.002 |
3- |
8 |
-6.548 |
0.535 |
7.619 |
4.722 |
4.722 |
-22.261 |
-22.261 |
6- |
9 |
-8.160 |
0.137 |
8.434 |
5.531 |
5.531 |
-14.648 |
-14.648 |
|
|
|
|
|
|
|
|
|
