35) Системы произвольного числа нормальных законов на плоскости. Корреляционная матрица.

Когда главные оси рассеивания для всех законов, подлежащих композиции, параллельны друг другу, выбирая координатные оси параллельно этим главным осям рассеивания, мы будем иметь дело с системами независимых случайных величин, и композиция нормальных законов выполняется по простым формулам:

На практике часто встречаются случаи, когда в числе законов, подлежащих композиции, встречаются так называемые «вырожденные» законы, т. е. законы, характеризующиеся эллипсом рассеивания, имеющим только одну полуось (другая равна нулю). Такие «вырожденные» законы дают рассеивание только в одном направлении. При композиции таких законов нужно поступать так же, как при композиции обычных законов, полагая некоторые параметры (средние квадратические или вероятные отклонения) равными нулю. Все корреляционные моменты и дисперсии удобно расположить в виде прямоугольной таблицы (так называемой матрицы):

Из определения корреляционного момента ясно, что , т. е. элементы корреляционной матрицы, расположенные симметрично по отношению к  главной  диагонали, равны. В связи с этим часто заполняется не вся корреляционная матрица, а лишь ее половина, считая от главной диагонали:

.

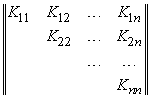В случае, когда случайные величины  не коррелированы, все элементы корреляционной матрицы, кроме диагональных, равны нулю:

.

36) Матожидание и дисперсия для линейной функции случайных аргументов.

Дана система случайных величин , подчиненная нормальному закону распределения (или, короче, «распределенная нормально»); случайная величина  представляет собой линейную функцию этих величин:

, . На практике часто встречается случай, когда законы распределения случайных величин , входящих в формулу (12.7.1), в точности не известны, а известны только их числовые характеристики: математические ожидания и дисперсии. Если при этом величины  независимы, а их число n достаточно велико, тo, как правило, можно утверждать, что, безотносительно к виду законов распределения величин X_i, закон распределения величины Y близок к нормальному.

37) Закон больших чисел. Неравенство Чебышева.

Пусть имеется случайная величина  с математическим ожиданием  и дисперсией . Неравенство Чебышева утверждает, что, каково бы ни было положительное число , вероятность того, что величина  отклонится от своего математического ожидания не меньше чем на , ограничена сверху величиной :

.

ЗБЧ: При достаточно большом числе независимых опытов среднее арифметическое наблюденных значении случайной величины сходится по вероятности к ее математическому ожиданию. .

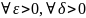
Запишем в аналогичной форме теорему Чебышева. Она утверждает, что при увеличении  среднее арифметическое  сходится по вероятности к , т. е.

Доказательство. Величина имеет числовые характеристики ; .

Применим к случайной величине  неравенство Чебышева, полагая :

.

Как бы мало ни было число , можно взять  таким большим, чтобы выполнялось неравенство , откуда .

38) Теорема Маркова.

Обобщенная теорема Чебышева формулируется следующим образом. Если

 - независимые случайные величины с математическими ожиданиями

и дисперсиями . Если все дисперсии ограничены сверху одним и тем же числом :       ,                              

то при возрастании  среднее арифметическое наблюденных значений величин  сходится по вероятности к среднему арифметическому их математических ожиданий. Т.е.

Доказательство. Рассмотрим величину .

Ее математическое ожидание равно: , а дисперсия .

Применим к величине  неравенство Чебышева:

,

или

.    

Заменим в правой части неравенства (13.4.2) каждую из величин  большей величиной . Тогда неравенство только усилится:

.

Как бы мало ни было , можно выбрать  настолько большим, чтобы выполнялось неравенство

;

тогда

.

Переходя к обратному событию, получим требуемую формулу.