4. Обобщенно - однородные уравнения.

 Рассмотрим уравнения вида

                                                                   .                                                               (5)

Уравнение (5) называется обобщенно - однородным, если существуют числа k и m такие, что

.

С помощью замены (при x<0 полагаем  )

,

где t - новая независимая переменная, u - новая искомая функция, уравнение (5) приводит к уравнению, не содержащему независимой переменной t и, следовательно, допускающему понижение порядка на единицу (см. п. 2).

Производные при данной замене преобразуются по формулам

......................................................................

.

Подстановка последних равенств в (5) дает уравнение вида

,

которое явно не содержит независимую переменную t.

Пример 4.  Решить уравнение  .

Решение.

Проверим, что уравнение является однородным. С этой целью вместо переменных   подставим в выражение для функции  соответственно   и, если это возможно, подберем значение k таким образом, чтобы выполнялось тождество

.

Очевидно, что такое тождество выполняется лишь при условии 4k=2, т.е при k=1/2 (при этом m=2). Следовательно, данное уравнение обобщенно однородное. Применив подстановку  , получим уравнение

.

Последнее уравнение явно не содержит переменную t, поэтому посредством замены   понижаем порядок на единицу:

.

Проинтегрировав последнее уравнение, находим

.

Далее, интегрируем уравнение

:

и получаем окончательно решения уравнение в виде

.

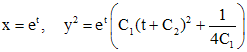5. Уравнение в точных производных.

 Рассмотрим уравнения вида

                                                                   ,                                                               (1)

левые части которых являются точными производными от некоторой функции  , т.е.

.

Такие уравнения называются уравнениями в точных производных. Из последнего равенства следует, что соотношение

является первым интегралом уравнения (1) - уравнением (n-1) - го порядка относительно искомой функции. Таким образом, уравнение в точных производных допускают понижение порядка на единицу.

Пример 5.  Решить уравнение  .

Решение.

Имеем

  ,

откуда следует, что

,

или

.

Это линейное уравнение первого порядка, и его общее решение имеет вид

.

27 Линейные однородные уравнения. Определения и общие свойства.

Используя свойства линейного дифференциального оператора, сформулируем свойство решений линейного дифференциального уравнения (4), которое дает ключ к пониманию структуры (устройства) общего решения.

 

Если  h(x)  и  g(x)  решения линейного однородного уравнения (4), то для любых констант С₁ и С₂ функция (х) = С₁h(x) + С₂g(x)  решение уравнения (4).

 

Известно, что общее решение уравнения n-го порядка содержит n произвольных констант. В связи с этим возникают следующие вопросы. Можно ли найти такие n решений ₁(х), ₂(х), ..., _n(х), что функция

 

(х) = ,                                     (5)

 

где С_i  (i = 1, 2, ..., n)  константы, будет общим решением линейного однородного уравнения (4)? Какими свойствами должны обладать функции _i(х), чтобы составленная из них по формуле (5) функция являлась общим решением?

На основании свойства решений линейных однородных дифференциальных уравнений можно сделать вывод, что множество всех решений данного уравнения образует линейное пространство. Известно, что в любом линейном пространстве каждый элемент является линейной комбинацией базиса.

Введем понятия линейной зависимой и линейной независимой системы функций.

 

 

Определение 2

Система функций y₁(х), y₂(х), ..., y_m(х) называется линейно зависимой на интервале (a, b), если на этом интервале выполняется тождество:

 

₁y₁(х) + ₂ y₂(х) + ...+ _m y_m(х)   0,                        (6)

 

в котором, по крайней мере, один из коэффициентов _i (i = 1, 2, ..., m) отличен от нуля (₁² + ₂² + ... + _m²   0).