
- •Алгебра логики (булева алгебра).
- •Алгебра логики
- •Основные функции алгебры логики:
- •Формулы алгебры логики.
- •Равносильные формулы
- •Основные тождества (равносильные формулы) алгебры логики.
- •Двойственные функции
- •Полные системы функций (связок).
- •Дизъюнктивные и конъюнктивные нормальные формы.
- •Разложение функций алгебры логики по к переменным.
- •Совершенные нормальные формы.
- •Построения сднф и скнф.
- •1. Преобразование исходной формулы в днф (см выше):
- •2.Преобразование днф в сднф.
- •1. Преобразование исходной формулы в кнф.
- •2.Преобразование кнф в скнф.
- •Построение совершенных нормальных форм с помощью таблиц истинности
- •Построение совершенных нормальных форм, используя принцип двойственности.
- •Тавтологии и противоречия. Проблема разрешимости в алгебре логики. Логические следствия.
Тавтологии и противоречия. Проблема разрешимости в алгебре логики. Логические следствия.
Формула алгебры логики называется тождественно истиной, общезначимой или тавтологией, если она принимает значение 1 при всех значениях входящих в неё элементарных переменных.
Будем
обозначать тавтологию
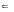 F,
где F - тождественно истинная формула,
а
-
обозначение тавтологии.
F,
где F - тождественно истинная формула,
а
-
обозначение тавтологии.
Примеры тавтологий: xx и x(yx).
Противоречием или тождественно ложной формулой в алгебре логики называют всякую формулу, которая принимает значение 0 при любых значениях входящих в неё элементарных переменных высказываний.
Пример противоречия: xx.
Формула алгебры логики называется выполнимой, если она принимает значение 1 хотя бы на одном наборе значений входящих в неё элементарных переменных высказываний.
Любая формула, не являющаяся противоречием, является выполнимой (и наоборот).
Проблема разрешимости в алгебре логики состоит в том, чтобы найти способ, позволяющий для любой формулы алгебры логики определить, является ли она тождественно истиной.
Очевидно, что эта проблема может быть решена путём построения для заданной формулы таблицы истинности. Однако, существует более эффективный способ решения этой проблемы.
Теорема о тождественной истинности формулы алгебры логики.
Для того, чтобы формула алгебры логики была тождественно истиной, необходимо и достаточно, чтобы каждая элементарная дизъюнкция её конъюнктивной нормальной формы содержала, по крайней мере, одно элементарное переменное высказывание вместе с его отрицанием.
Доказательство.
Пусть
каждая элементарная дизъюнкция КНФ,
равносильной исходной формуле, содержит
некоторую переменную вместе с её
отрицанием. Рассмотрим произвольную
элементарную дизъюнкцию и пусть в ней
содержится некоторая переменная x
и её отрицание
 ,
тогда, из-за того, что xV
=1,
эта элементарная конъюнкция будет
равна 1. Так для всех элементарных
конъюнкций КНФ.
,
тогда, из-за того, что xV
=1,
эта элементарная конъюнкция будет
равна 1. Так для всех элементарных
конъюнкций КНФ.
Пусть исходная формула является тождественно истиной. Рассмотрим КНФ ей равносильную и предположим, что в некоторой элементарной дизъюнкции этой КНФ нет пары типа x и . Тогда рассмотрим набор из 0 и 1, такой, что в этом наборе компонента равна 1, если в рассматриваемой элементарной дизъюнкции ей соответствующая переменная входит под знаком отрицания и равна 0, если соответствующая переменная входит без знака отрицания. Тогда на этом наборе элементарная дизъюнкция будет равна 0, тем самым и значение КНФ на этом наборе будет равно 0, что противоречит тожественной истинности исходной формулы.
Теорема о тождественной ложности формулы алгебры логики
Для того, чтобы формула алгебры логики была тождественно ложной, необходимо и достаточно, чтобы каждая элементарная конъюнкция её ДНФ содержала по крайней мере одно элементарное переменное высказывание вместе со своим отрицанием.
Доказательство аналогично доказательству предыдущей теоремы.
Формула алгебры логики f называется логическим следствием формул f1,f2,…,fm, если для любых наборов значений переменных, входящих в формулы, f1,f2,…,fm , f для которых истины все формулы f1,f2,…,fm, формула f тоже истина. Обозначение f1,f2,…,fm f.
Теорема о логическом следствии
Формула
алгебры логики f
является логическим следствием
формулы алгебры логики g,
тогда и только тогда, если
g f.
f.
Доказательство.
Пусть n - количество различных переменныхf, входящих в формулы g и f, и а n - мерный двоичный набор из 0 и 1.
Пусть
g
f
, покажем что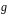


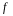 .
.
Так как f является следствием из g, то на любом наборе а, если g(а)=1, то f(а)=1. Если же g(а)=0, то 0 f принимает значение 1 при любом значенииf (а).
Пусть g f, покажем, что g f.
f- следствие из g, если при любом наборе а, из g(а)=1 следует f(а)=1.
Пусть а, такой набор, что g(а)=1, тогда из того, что g f- тождественно истинная формула, её значение на наборе а должно равняться 1, а это для операции импликации может быть лишь тогда, когда f (а)=1.
Теорема доказана.
Аналогичным образом доказывается и более общая теорема.
Обобщённая теорема о логическом следствии
f1,f2,…,fm
f
тогда и только тогда, если f1 f2
...
fm
f
f2
...
fm
f
Множество формул алгебры логики { f1,f2,…,fm } называется непротиворечивым, если существует по крайней мере один такой набор значений переменных, входящих в эти формулы, что все формулы из множества на этом наборе равны 1.
Множество формул алгебры логики { f1,f2,…,fm } называется противоречивым, если при всяком наборе значений переменных, входящих в эти формулы, по крайней мере одна из формул принимает значение 0.
Отсюда,
{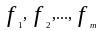 }
- непротиворечиво, если f1
f2
...
fm
=1 по крайней мере на одном наборе и
противоречиво, если f1
f2
...
fm
=0 для любого набора значений переменных.
}
- непротиворечиво, если f1
f2
...
fm
=1 по крайней мере на одном наборе и
противоречиво, если f1
f2
...
fm
=0 для любого набора значений переменных.
Теорема о противоречивости множества формул алгебры логики
Множество формул алгебры логики противоречиво, если из него в качестве логического следствия можно вывести противоречие.
Для доказательства теоремы используется теорема 4 и определение операции импликации.
Теорема о тождественной истинности формулы алгебры логики

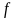 ,
если в качестве логического следствия
из
и
,
если в качестве логического следствия
из
и
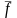 можно вывести противоречие.
можно вывести противоречие.
Основные схемы доказательств
Схема 1. «Если x то y»
Доказательство теорем типа “если x, то y”.
Схема доказательства основана на следующем логическом следствии:
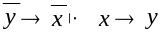 .
.
Действительно,
по теореме 5 из
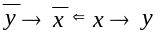 следует
следует
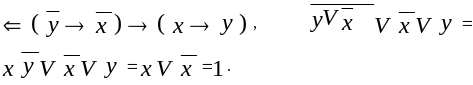
Схема 2. «доказательство от противного» или метод косвенного доказательства.
Схема доказательства основана на следующем логическом следствии:

Действительно, по теореме 6 из следует, что
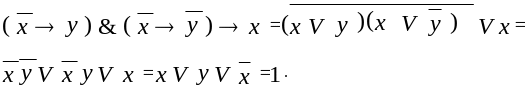
Схема 3 «доказательство построением цепочки импликаций»
Схема доказательства основана на следующем логическом следствии:

Действительно,
по теореме 6 из
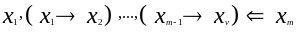 следует, что
следует, что

Схема 4. «Доказательство разбором случаев»
Схема доказательства основана на следующем логическом следствии:
 .
.
Действительно, по теореме 6 из следует, что

