
- •I. Элементы линейной и векторной алгебры, аналитической геометрии.
- •1. Определители второго и третьего порядков. Основные свойства. Минор и алгебраическое дополнение. Понятие определителя n-ого порядка и его вычисление.
- •Свойства определителей.
- •2. Матрицы, действия над матрицами. Обратная матрица. Ранг матрицы.
- •Основные действия над матрицами.
- •Обратная матрица.
- •Свойства обратных матриц.
- •3. Системы линейных уравнений. Теорема Кронекера-Капелли (формулировка). Правило Крамера.
- •Элементарные преобразования систем.
- •Теорема Кронекера – Капелли. (условие совместности системы)
- •Метод Крамера.
- •4. Решение систем линейных уравнений матричным методом.
- •5. Метод Гаусса. Однородные системы линейных уравнений и их решение. Метод Гаусса.
- •Однородные системы линейных уравнений
- •6. Векторы. Линейные операции над векторами и их свойства.
- •Свойства векторов.
- •7. Проекция вектора на ось. Свойства проекций.
- •Некоторые свойства проекций
- •8. Линейная зависимость векторов. Разложение вектора по базису. Линейная зависимость векторов.
- •9. Декартова система координат. Координаты вектора. Система координат.
- •Декартова система координат.
- •Линейные операции над векторами в координатах.
- •10. Направляющие косинусы, длина вектора.
- •11. Деление отрезка в данном отношении.
- •12. Скалярное произведение векторов, его свойства, вычисление и применение.
- •13. Векторное произведение векторов, его свойства, вычисление и применение.
- •Свойства векторного произведения векторов:
- •14. Смешенное произведение векторов, его свойства, вычисление и применение.
- •Свойства смешанного произведения:
- •15. Прямая линия на плоскости. Различные способы задания. Взаимное расположение прямых на плоскости. Расстояние от точки до прямой на плоскости. Уравнение линии на плоскости.
- •Уравнение прямой на плоскости.
- •Уравнение прямой по точке и вектору нормали.
- •Уравнение прямой по точке и направляющему вектору.
- •Параметрическое уравнение прямой
- •Уравнение прямой, проходящей через две точки.
- •2. Условие перпендикулярности.
- •16. Плоскость в пространстве. Различные способы задания. Взаимное расположение плоскостей. Расстояние от точки до плоскости. Общее уравнение плоскости.
- •Уравнение плоскости по точке и вектору нормали.
- •Уравнение плоскости в отрезках.
- •Уравнение плоскости, проходящей через три точки.
- •17. Прямая в пространстве. Различные способы задания. Взаимное расположение прямых в пространстве. Уравнение прямой в пространстве по точке и направляющему вектору.
- •Уравнение прямой в пространстве, проходящей через две точки.
- •Общие уравнения прямой в пространстве.
- •Условия параллельности и перпендикулярности прямых в пространстве.
- •Угол между прямыми в пространстве.
- •18. Взаимное расположение прямой и плоскости в пространстве. Угол между прямой и плоскостью.
- •Условия параллельности и перпендикулярности прямой и плоскости в пространстве.
- •Эллипс.
- •Гипербола.
- •Парабола.
- •20. Поверхности второго порядка. Цилиндрические поверхности. Исследование поверхностей методом сечений. Поверхности второго порядка.
- •С фера:
- •К онус второго порядка:
- •Двуполостный гиперболоид:
- •Эллиптический параболоид:
- •Г иперболический параболоид:
- •II. Введение в математический анализ
- •21. Множество действительных чисел.
- •Операции над множествами.
- •22. Функция, область ее определения и способы задания. Сложные и обратные функции.
- •Способы задания функций
- •Сложная функция.
- •Обратная функция.
- •23. Свойства (четность, периодичность, монотонность, ограниченность) и графики функций.
- •24. Гиперболические функции, их свойства и графики.
- •25. Числовые последовательности. Предел числовой последовательности.
- •Ограниченные и неограниченные последовательности.
- •26. Число е. Натуральные логарифмы.
- •Связь натурального и десятичного логарифмов.
- •2 7. Предел функции в точке, односторонние пределы. Геометрическая иллюстрация определений.
- •28. Предел функции в бесконечности. Геометрическая иллюстрация.
- •29. Бесконечно малые функции и их свойства. Бесконечно большие функции. Связь между бесконечно малыми и бесконечно большими функциями.
- •Бесконечно большие функции и их связь с бесконечно малыми.
- •30. Основные теоремы о пределах.
- •Теорема доказана.
- •31. Первый и второй замечательные пределы.
- •32. Сравнение бесконечно малых функций.
- •33. Непрерывность функций в точке и на отрезке. Точки разрыва функции и их классификация.
- •Точки разрыва и их классификация.
- •Непрерывность функции на интервале и на отрезке.
- •34. Свойства функций непрерывных в точке.
- •Непрерывность некоторых элементарных функций.
- •35. Свойства функций непрерывных на отрезке (теоремы Вейерштрасса, Коши, о промежуточных значениях) и их геометрических смысл.
- •III. Дифференциальное исчисление функции одной переменной.
- •36. Задачи, приводящие к определению производной.
- •37. Производная функции, ее геометрический и механический смыслы.
- •38. Односторонние производные. Производная сложной и обратной функции. Односторонние производные функции в точке.
- •Производная сложной функции.
- •Производная обратных функций.
- •Основные правила дифференцирования.
- •Производные основных элементарных функций.
- •Дифференциал функции.
- •42. Свойства дифференциала и инвариантность его формулы. Применение дифференциала к приближенным вычислениям.
- •Применение дифференциала к приближенным вычислениям.
- •43. Производные и дифференциалы высших порядков. Производные и дифференциалы высших порядков.
- •Общие правила нахождения высших производных.
- •44. Основные теоремы дифференциального исчисления: Ролля (с доказательством), Коши (без доказательства), Лагранжа (с доказательством). Теорема Ролля
- •Теорема Коши.
- •Теорема Лагранжа.
- •45. Правило Лопиталя (доказательство для случая неопределенности ). Правило Лопиталя.
- •Точки экстремума.
- •Асимптоты.
- •Вертикальные асимптоты.
- •Наклонные асимптоты.
20. Поверхности второго порядка. Цилиндрические поверхности. Исследование поверхностей методом сечений. Поверхности второго порядка.
Уравнение плоскости в пространстве характеризуется тем, что все переменные входят в степенях не выше первой. Поэтому плоскость является поверхностью 1го порядка. Если в уравнение поверхности хотя бы одна переменная входит во 2й степени, то говорят о поверхностях 2го порядка.
С фера:
Определение. Поверхности второго порядка – это поверхности, уравнения которых в прямоугольной системе координат являются уравнениями второго порядка.
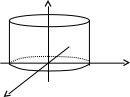
Цилиндрические поверхности.
Определение. Цилиндрическими поверхностями называются поверхности, образованные множеством параллельных прямых (образующих), проходящих через все точки некоторой фиксированной линии (направляющей).
Рассмотрим поверхности, в уравнении которых отсутствует составляющая z, т.е. направляющие параллельны оси Оz. Тип линии на плоскости ХOY (эта линия называется направляющей поверхности) определяет характер цилиндрической поверхности. Рассмотрим некоторые частные случаи в зависимости от уравнения направляющих:
- эллиптический цилиндр.
2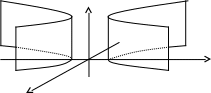 )
- гиперболический
цилиндр.
)
- гиперболический
цилиндр.
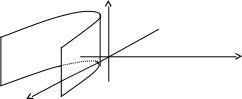
x2 = 2py – параболический цилиндр.
Конической поверхностью называется множество прямых (образующих), проходящих через некоторые точки вершины и пересекающие некоторую линию (направляющую).
К онус второго порядка:
Э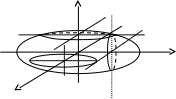 ллипсоид
– поверхность, которая подходящим
образом подобрана в системе координат
и имеет уравнение
ллипсоид
– поверхность, которая подходящим
образом подобрана в системе координат
и имеет уравнение
![]()
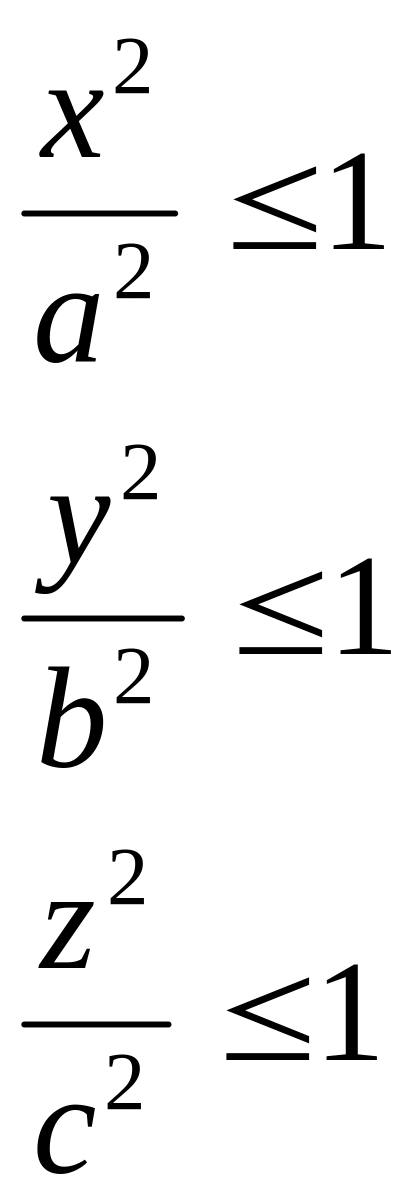 т.к.
в уравнение текущие координаты входят
в четных степенях, то эллипсоид симметричен
относительно координатных плоскостей.
Числа
т.к.
в уравнение текущие координаты входят
в четных степенях, то эллипсоид симметричен
относительно координатных плоскостей.
Числа
![]() полуоси эллипсоида.
полуоси эллипсоида.
Чтобы установить форму эллипсоида, будем пересекать его плоскостями, параллельными координатным плоскостям.
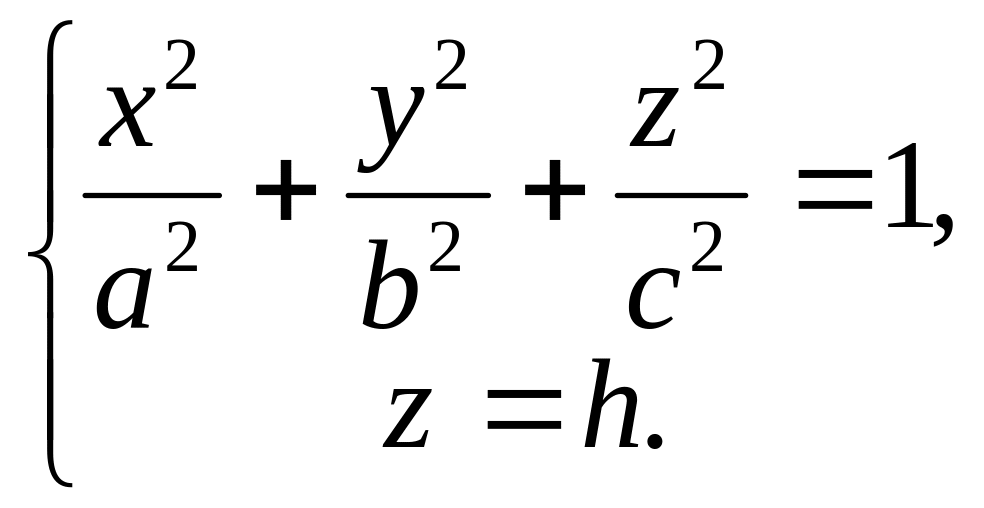 пересечем
плоскостью
пересечем
плоскостью
![]() .
.
Если
линия лежит на
![]() ,
то
,
то
![]() отсутствует,
значит, линия пересечения будет иметь
вид:
отсутствует,
значит, линия пересечения будет иметь
вид:
![]() .
При
.
При
![]() получается эллипс с полуосями
получается эллипс с полуосями
![]() и
и
![]() .
.
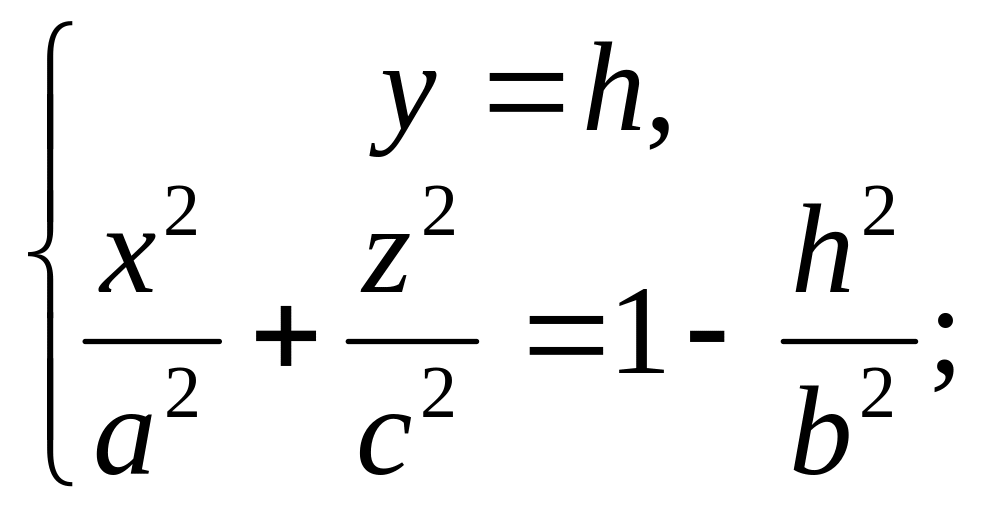
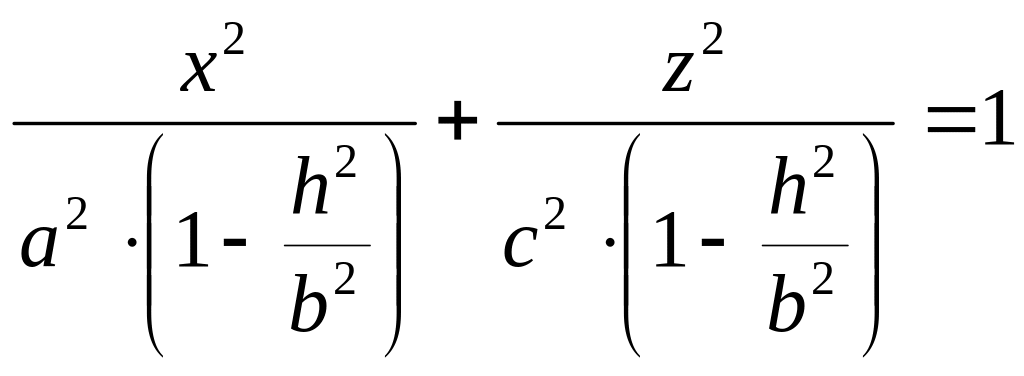 эллипс.
эллипс.
Аналогично
рассекаем плоскостью
![]() .
.
Пересечение эллипсоида любой поверхностью дает эллипс.
О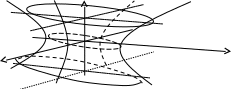 днополостный
гиперболоид –
плоскость, которая в подходящим образом
подобранной системе координат задается
уравнением:
днополостный
гиперболоид –
плоскость, которая в подходящим образом
подобранной системе координат задается
уравнением:
![]()
Имеет 3 плоскости симметрии (координатные плоскости).
Будем пересекать поверхность плоскостями, параллельными координатным плоскостям.
 эллипс
с полуосями
и
.
эллипс
с полуосями
и
.
 при
любых
при
любых
![]() правая часть >0. чем больше
,
тем больше полуоси эллипса.
правая часть >0. чем больше
,
тем больше полуоси эллипса.
Сечение такой поверхности плоскостью всегда дает эллипс.
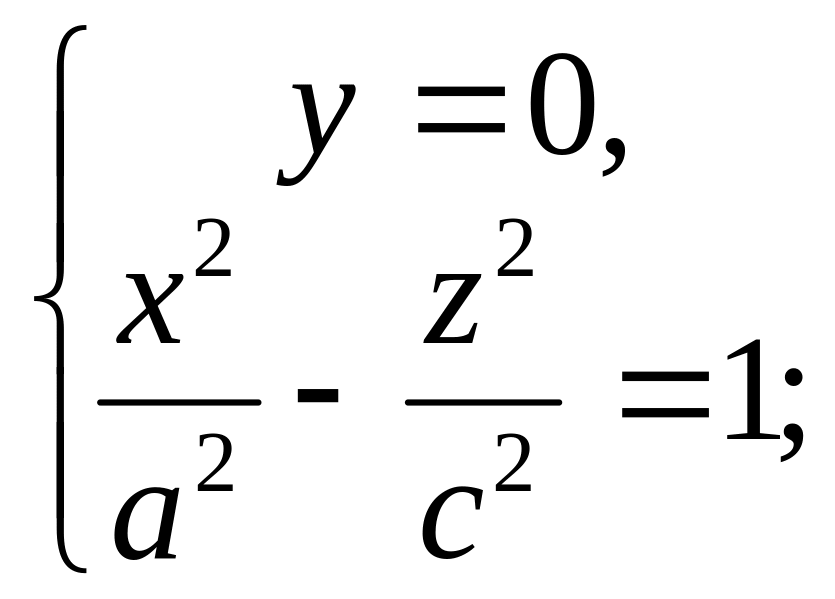 гипербола.
гипербола.
 Если
Если
![]() ,
то в сечении гипербола, у которой
действительная ось – ось ОХ. Если
,
то в сечении гипербола, у которой
действительная ось – ось ОХ. Если
![]() ,
то в сечении гипербола, у которой
действительная ось
,
то в сечении гипербола, у которой
действительная ось
![]() .
.
 гипербола,
у которой действительная ось
,
а мнимая
гипербола,
у которой действительная ось
,
а мнимая
![]() .
.
 в
зависимости от знака правой части
получается либо гипербола с действительной
осью
,
либо гипербола с действительной осью
в
зависимости от знака правой части
получается либо гипербола с действительной
осью
,
либо гипербола с действительной осью
![]() .
.
