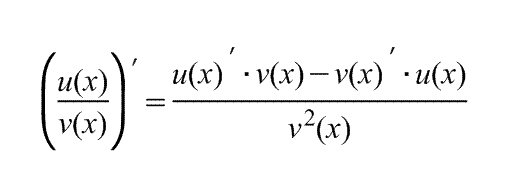- •Определители 2-го, 3-го и n-го порядков, их свойства и методы вычисления.
- •Системы линейных алгебраических уравнений, методы их решения: метод Крамера
- •Скалярное произведение векторов, его основные свойства, выражение через координаты перемножаемых векторов.
- •Векторное произведение векторов, его основные свойства, выражение через координаты перемножаемых векторов.
- •Условие компланарности векторов в координатной форме:
- •Декартовы и полярные координаты на плоскости. Уравнения линий в декартовых, полярных координатах и в параметрическом виде. Примеры.
- •Прямая в пространстве и ее основные уравнения: векторно-параметрическое, канонические, по двум точкам, общие уравнения (пара пересекающихся плоскостей).
- •Кривые 2-го порядка: окружность, эллипс, гипербола, парабола и их уравнения в декартовых и полярных координатах, в параметрическом виде.
- •Поверхности и их уравнения в пространстве. Каноническая теория поверхностей 2-го порядка: геометрические свойства и исследование их формы методом сечений. Уравнения поверхностей вращения.
- •Множество действительных чисел. Числовые последовательности, их пределы.
- •Свойства пределов функции:
Свойства пределов функции:
-
Предел суммы/разности двух функций равен сумме/разности их пределов:
![]()
-
Предел произведения двух функций равен произведению их пределов:
![]()
-
Предел частного двух функций равен частному их пределов, при условии, что предел знаменателя не равен нулю:
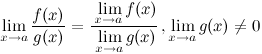
-
Константу можно выносить за знак предела:
![]()
-
Предел степени с натуральным показателем равен степени предела:
![]()
Функция
 называется
бесконечно
малой
при
называется
бесконечно
малой
при
 ,
если
,
если
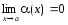 .
.
Функция
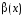 называется
бесконечно
большой при
называется
бесконечно
большой при
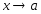 ,
если
,
если
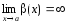 .
.
Теорема.
Если
функция
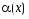 —
бесконечно малая при
—
бесконечно малая при
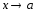 ,
то
,
то
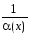 —
бесконечно большая функция при
—
бесконечно большая функция при
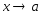
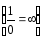 .
.
Если
функция
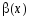 — бесконечно большая при
— бесконечно большая при
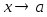 ,
то
,
то
 - бесконечно малая функция при
- бесконечно малая функция при
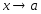 (
(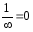 ).
).
Справедливы следующие утверждения:
-
Сумма конечного числа бесконечно малых функций есть бесконечно малая функция.
-
Произведение ограниченной функции на бесконечно малую есть бесконечно малая функция.
-
Произведение конечного числа бесконечно малых функций есть бесконечно малая функция.
Теоремы о пределах
Если
пределы
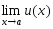 и
и
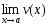 существуют
и конечны, то
существуют
и конечны, то
-
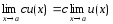 ,
где с
– const;
,
где с
– const; -
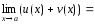
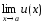 +
+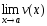 ;
; -
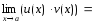
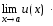
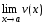 ;
; -
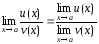 ,
где
,
где
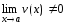 .
.
Замечательные пределы.
-
Первый замечательный предел:
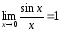 .
.
-
Второй замечательный предел:
 ,
,
 — иррациональное
число,
— иррациональное
число,
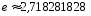 — одна из фундаментальных величин в
математике. Функция
— одна из фундаментальных величин в
математике. Функция
 называется экспонентой;
называется экспонентой;
 называется натуральным
логарифмом.
называется натуральным
логарифмом.
Для
сравнения двух бесконечно малых функций
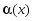 и
и
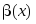 в
точке
в
точке
 находят
предел отношения
находят
предел отношения
 .
.
Если
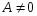 и
и
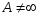 ,
то
функции
,
то
функции
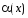 и
и
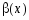 называются бесконечно
малыми одного порядка.
называются бесконечно
малыми одного порядка.
Если
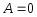 ,
то
,
то
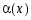 называется
бесконечно
малой высшего порядка по сравнению с
называется
бесконечно
малой высшего порядка по сравнению с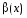 .
Записывается
это так:
.
Записывается
это так:
 .
.
Если
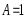 ,
то бесконечно малые функции
,
то бесконечно малые функции
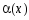 и
и
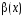 называют эквивалентным
и обозначают
называют эквивалентным
и обозначают
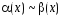 .
.
Основные
эквивалентности
при
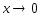 :
:
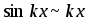 ,
,
 ,
,
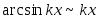 ,
,
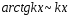 ,
,
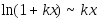 ,
,
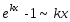 .
.
Предел отношения двух бесконечно малых функций в некоторой точке равен пределу отношения эквивалентных им бесконечно малых функций в той же точке.
-
Непрерывность функции в точке, интервале, на отрезке. Непрерывность основных элементарных и элементарных функций в области их определения. Точки разрыва функции и их классификация. Свойства функций, непрерывных на отрезке.
Функция
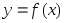 называется непрерывной
в точке
называется непрерывной
в точке
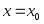 ,
если предел функции в точке
,
если предел функции в точке
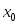 существует и
существует и
 .
.
Функция
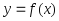 называется непрерывной
в точке
называется непрерывной
в точке
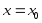 ,
если существуют односторонние пределы
в точке
,
если существуют односторонние пределы
в точке
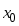 и
и
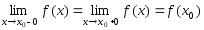 .
.
Если
хотя бы один из этих односторонних
пределов не существует или равен
бесконечности, то
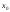 называется точкой
разрыва второго рода.
называется точкой
разрыва второго рода.
Если
функция непрерывна во всех точках
отрезка
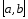 ,
то она называется непрерывной
на этом отрезке
,
то она называется непрерывной
на этом отрезке
Теорема
I.
Если
функции
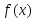 и
и
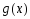 непрерывны в точке
непрерывны в точке
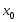 ,
то в этой точке непрерывны функции
,
то в этой точке непрерывны функции
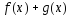 ,
,
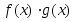 ,
,
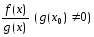 .
.
Теорема II. Сложная функция, составленная из непрерывных функций, непрерывна в соответствующей точке.
Теорема III. Всякая элементарная функция непрерывна в каждой точке своей области определения.
Теорема
1 (о сохранении знака непрерывной
функции). Если
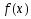 непрерывная
в точке х0
и
непрерывная
в точке х0
и

0,
то существует интервал, которому
принадлежит точка х0,,
где
функция
0,
то существует интервал, которому
принадлежит точка х0,,
где
функция
 имеет тот же знак,. что и
имеет тот же знак,. что и
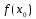 .
.
Теорема
2 (о наибольшем, наименьшем и промежуточных
значениях непрерывной функции).
Непрерывная на отрезке
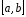 функция
функция
 достигает
на этом отрезке наибольшего М и наименьшего
m
значения, а также принимает все свои
промежуточные значения, т.е. для
произвольного
достигает
на этом отрезке наибольшего М и наименьшего
m
значения, а также принимает все свои
промежуточные значения, т.е. для
произвольного
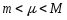 существует
хотя бы одно значение
существует
хотя бы одно значение
 такое, что
такое, что
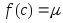
Теорема
3 (о нулях непрерывной функции).
Если функция
 непрерывна
на отрезке
непрерывна
на отрезке
 и на концах отрезка принимает значения
противоположных знаков, т.е.
и на концах отрезка принимает значения
противоположных знаков, т.е.
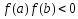 ,то
существует хотя бы одно значение х0
,то
существует хотя бы одно значение х0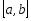 такое, что
такое, что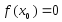 (существует
корень уравнения
(существует
корень уравнения
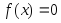
-
Производная функции, её смысл (геометрический, физический, экономический). Производная суммы, разности, произведения, частного функций, сложной и обратной функций. Таблица производных основных элементарных функций. Уравнения касательной и нормали к графику функции.
Производной
функции
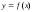 в точке х называется предел
отношения приращения функции
в точке х называется предел
отношения приращения функции
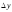 к приращению аргумента
к приращению аргумента
 ,
когда
,
когда
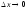 ,
т.е.
,
т.е.
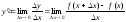 .
.
Для
производной функции
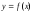 в точке х применяют также обозначения:
в точке х применяют также обозначения:
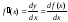 .
.
Функция, имеющая в данной точке конечную производную, называется дифференцируемой в этой точке.
Геометрический смысл производной
производная
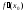 функции
функции
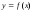 равна угловому коэффициенту касательной
к графику этой функции в точке с абсциссой
равна угловому коэффициенту касательной
к графику этой функции в точке с абсциссой
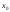 .
.
Уравнение
касательной к кривой
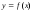 в точке
в точке
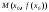 имеет вид
имеет вид
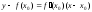 ,
,
а
уравнение нормали к данной кривой
в этой же точке записывается в виде
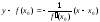 при условии, что
при условии, что
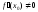 .
.
Если
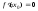 ,
то уравнение касательной:
,
то уравнение касательной:
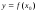 ,
а уравнение нормали:
,
а уравнение нормали:
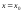 .
.
Механический
смысл производной. Пусть материальная
точка движется прямолинейно по закону
 .
Тогда
.
Тогда
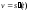 ,
т.е. производная от пути по времени
есть скорость движения точки.
,
т.е. производная от пути по времени
есть скорость движения точки.
Производная суммы равна сумме производных.
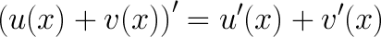
Производная разности равна разности производных
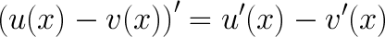
Производная произведения находится по формуле (uv)'=u'v+v'u
Производная чатсного