5.6. Решение краевых задач для обыкновенных дифференциальных уравнений.
Краевая задача отличается от задачи Коши для системы обыкновенных дифференциальных уравнения (ОДУ) способом задания начальных условий. В задаче Коши, как известно [ ], все n –начальных условий, необходимых для определения постоянных интегрирования, задаются на одном(левом или правом) конце интервала интегрирования, а в краевой задаче – m-условий может быть задано на левом конце, а оставшиеся n-m условий - на правом конце интервала.
Основным методом решения краевой задачи является метод прогонки. Существо метода состоит в определении методом последовательных приближений недостающих начальных условий на левом конце интервала интегрирования и сведение, таким образом, краевой задачи к эквивалентной ей задаче Коши. В Mathcad алгоритм метода прогонки реализуется с помощью функции sbval.
Следует отметить, что функция sbval выполняет только преобразование граничных условий, заданных на правом конце интервала интегрирования в эквивалентные им недостающие начальные условия, освобождая тем самым пользователя от необходимости программировать алгоритм метода, но не производит решения системы уравнений. Для решения системы после того, когда определены начальные условия, для решения системы уравнений применим любой из рассмотренных выше методов решения ОДУ.
Обращение к функции имеет вид: sbval(z, t0, t1, D, load, score). Аргументами функции являются:
z – вектор значений начальных приближений для значений недостающих начальных условий на левом конце интервала интегрирования (в точке t0);
D(t,y) – вектор правых частей (вектор производных) системы уравнений, записанных в символическом виде;
load(t0, z) – векторная функция, содержащая m – заданных начальных условий на левом конце интервала интегрирования(в точке t0) и n-m неизвестных начальных условий, которые должны определяться функцией sbval;
score(t1, y0 ) – невязка, вычисляемая функцией sbval, представляет собой векторную функцию, каждый элемент которой содержит разность найденного приближённого решения на правом конце интервала интегрирования(в точке t1) и заданного граничного условия в этой точке.
Рис. 5. 8. Пример решения краевой задачи для ОДУ.
Для решения краевой задачи с использованием функции sbval необходимо:
- записать в символьной форме вектор правых частей (вектор производных) решаемой системы уравнений;
- задать вектор начальных условий (вектор z), элементами которого являются как известные (заданные в виде констант) начальные условия, так и подлежащие определению, записанные в символьном виде (в виде идентификаторов с нижним индексом);
- задать (присвоить) начальное приближение для недостающих начальных условий;
- присвоить функции score имя решения на правом конце интервала интегрирования, для которого задано начальное условие;
- присвоить функции load значение вектора приближения начальных условий (вектор z);
- назначить имя вектору результата расчёта начальных условий, например S, и записать оператор: S:= sbval (z, t0, t1, load, score);
- записать обращение к функции или решающему блоку интегрирования системы ОДУ, указав в списке аргументов функции имя S в качестве имени вектора начальных условий;
- все дальнейшие действия по обработке решения ОДУ выполняются в соответствие с принятым способом решения задачи Коши(rkfixed , Rkadapt, Bulstoer или Radau).
В приведённом на рис. 5.8 примере решения краевой задачи для системы 3-х ОДУ, заданным является одно начальное условие z0(t0), заданное на левом конце интервала интегрирования и два краевых условия, которые пересчитываются функцией sbval в начальные условия. Дальнейшее решение осуществляется методом Рунге-Кутта с автоматическим выбором шага Rkadapt.
Как Находят, решение Odesolve может также использоваться parametrically в пределах решенного блока.
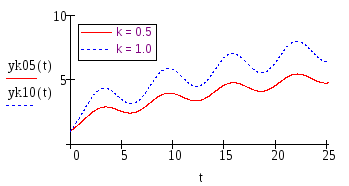
Результатом fy (k) является функция от функции, поэтому необходимо задавать значение параметра, для которого отыскивается решение. Этот результат назначен на обычное имя функции без независимой переменной t.
Поочередно, используйте оператор приставки от панели инструментов Evalutive( Оценка), чтобы вставить функцию единственного{отдельного} аргумента{спора}, но этот метод намного медленнее, чтобы вычислить, так как это повторно вычисляет целое, решают блок для каждого пункта{точки} данных.
является тем же самым как
rkfixed, Rkadapt, Bulstoer, и Radau
Другой способ решить отличительное уравнение - при использовании функции rkfixed.
Определите solver параметры:
Вектор начальных значений решения
Производная функция (Примечание: вторым аргументом должен быть вектор неизвестных значений функции.)
Матрица решения:
Отметьте: функция rkfixed , Rkadapt, Bulstoer, или Radau могла также использоваться здесь.
Независимые переменные ценности
Ценности функции решения
Результаты Odesolve - только интерполированная версия следствий функции единственной линии solvers. Решенная версия Блока позволяет более естественное примечание для проблемы, в то время как функция, возвращенная Odesolve - вставка того же самого таблицы, который возвращен единственной линией solver.
Можно правым щелчком на команде Odesolve выбрать другой решающий блок( solvers), например,с rkfixed, rkadapt, или radau.
Войдите в желательные параметры решения:
Конечная точка интервала решения
