
- •Глава 1. Процентные ставки
- •§1. Простые проценты, процентные и дисконтные ставки
- •§2. Определение срока ссуды и простой процентной ставки наращения.
- •§3. Дисконтирование и учёт по простой процентной ставке
- •§4. Сложная процентная ставка
- •§5. Номинальная процентная ставка
- •§6. Дисконтирование по сложной процентной ставке и сложная учётная ставка
- •§7. Непрерывное начисление сложных процентов
- •§8. Непрерывное дисконтирование по сложной учетной ставке
- •§9. Сравнение методов наращения.
- •§10. Переменные процентные ставки
- •§11. Начисление простых процентов в условиях инфляции.
- •§12. Начисление сложных процентов в условиях инфляции.
- •§13. Измерение реальной ставки процента в условии инфляции
- •§14. Начисление процентов в условиях налогообложения
- •Глава 2. Потоки платежей
- •§1. Потоки платежей. Основные характеристики потока платежей
- •§2. Финансовые ренты и их классификация
- •§3. Формулы наращённой суммы
- •§4. Формулы современной величины
- •§5. Определение параметров ренты
- •Глава 3. Вопросы измерения конечных финансовых результатов операций
- •§1. Эквивалентные серии платежей
- •§2. Номинальные и эффективные процентные ставки
- •§3. Оценка эффективности инвестиционных проектов
- •§4. Методы сравнения коммерческих контрактов
- •Глава 4. Практические приложения
- •§1. Кредитные расчёты
- •§2. Конверсия валюты и начисление процентов
§7. Непрерывное начисление сложных процентов
Если периоды начисления процентов в формуле использования номинальной процентной ставки (1.5.1) постоянно уменьшать, то количество этих периодов будет увеличиваться и, в конечном счете, будет стремиться к бесконечности. Следовательно, начисление процентов будет происходить непрерывно.
Таким образом,
непрерывное начисление процентов
− это начисление процентов за бесконечно
малые отрезки времени, т.е. при
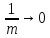 (или при m → ∞).
(или при m → ∞).
В случае непрерывного начисления сложных процентов годовая номинальная процентная ставка обозначается через δ, называется силой роста и представляет собой номинальную процентную ставку при начислении процентов за бесконечно малые отрезки времени. Другое название δ − интенсивность процентов или непрерывная процентная ставка.
Для вывода формулы определения наращённой суммы при постоянной интенсивности процентов в единицу времени δ в течение n периодов перейдём к пределу при m → ∞ в формуле (1.5.1) и заменим процентную ставку i(m) на δ:

Следовательно,
S = P0 · e n δ. (1.7.1)
§8. Непрерывное дисконтирование по сложной учетной ставке
В случае, когда
дисконтирование производится на
бесконечно малых отрезках времени, т.е.
при
 (или при m → ∞)
номинальные процентные ставки i(m)
и d(m)
при m → ∞ перестают
различаться. Поэтому при m → ∞
пользуются одной процентной ставкой -
силой роста δ.
(или при m → ∞)
номинальные процентные ставки i(m)
и d(m)
при m → ∞ перестают
различаться. Поэтому при m → ∞
пользуются одной процентной ставкой -
силой роста δ.
Формула, используемая при непрерывном дисконтировании, имеет вид:
P0 = Sn · e -n. (1.8.1)
§9. Сравнение методов наращения.
Экономический смысл множителя наращения заключается в следующем. Если срок долга n единиц времени, то множитель наращения показывает накопленную к моменту n будущую стоимость 1 д.е., вложенной в момент t = 0 на срок n (множитель наращения больше 1). Интенсивность процесса наращения определяется множителем наращения. Сравнивая эти множители для каждого значения срока n, можно определить эффективную ставку по известной процентной (дисконтной) ставке.
Все рассмотренные методы наращения приведены в таблице.
|
Метод наращения |
Формула |
Множитель наращения |
|
По простой процентной ставке i |
Sn = P0 (1 + n · i) |
(1 + n · i) |
|
По сложной процентной ставке i |
Sn = P0(1 + i)n |
(1 + i)n |
|
По номинальной процентной ставке i(m) |
Sn
= P0
·
|
|
|
По постоянной силе роста δ |
S = P0 · e n δ |
e n δ |
|
По номинальной учетной ставке d(m) |
|
|
|
По сложной учетной ставке d |
|
|
|
По простой учетной ставке d |
|
|
§10. Переменные процентные ставки
Если процентная ставка изменяет свое значение в течение срока долга, то она называется переменной.
При наращении по простой переменной процентной ставке используются следующие формулы:
Проценты за каждый период nj в сроке долга составляют
I(nj) = P0 nj ij, j = 1, ,2, …, k. (1.10.1)
Проценты за весь срок долга имеют вид:
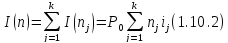
Тогда наращенная сумма к концу срока долга n составит:
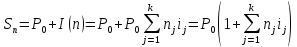
Следовательно,
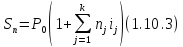
Пусть известна сумма погашаемого долга Sn, тогда можно найти первоначальную сумму, используя математическое дисконтирование по простой переменной процентной ставке:
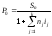 (1.10.4)
(1.10.4)
Формула нахождения первоначальной суммы долга по простой переменной учетной ставке имеет вид:

Формула наращенной суммы долга по простой переменной учетной ставке имеет вид:
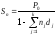 (1.10.6)
(1.10.6)
При наращении по сложной переменной процентной ставке формула наращенной суммы долга имеет вид:
 (1.10.7)
(1.10.7)
Если известна сумма погашаемого долга Sn, то, формулы приведенной к моменту t = 0 величины суммы Sn при математическом ее учете по сложной переменной процентной ставке имеют вид:
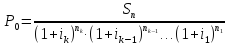 (1.10.8)
(1.10.8)
При банковском учёте формула для нахождения первоначальной суммы имеет вид:
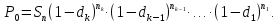 (1.10.9)
(1.10.9)
Рассмотрим наращение и дисконтирование по непрерывным переменным процентным ставкам.
Если наращение процентов является непрерывным, то используется сила роста или интенсивность процентов δ(t), являющаяся функцией времени. Если задан конкретный вид зависимости δ(t), то можно смоделировать поведение интенсивности процентов во времени.
Введём некоторые обозначения:
Пусть F(t) и ν(t) множитель наращения и дисконтный множитель соответственно по переменной силе роста δ(t) в момент t, где t ≥ 0.
F(t) – представляет собой накопление (стоимость) в момент t единичного вклада, сделанного в момент t = 0.
ν(t) - это современная стоимость 1 д.е., подлежащей выплате в момент t.
Множитель наращения для вклада, сделанного в момент t = 0, находится по формуле:
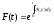 (1.10.10)
(1.10.10)
Дисконтный множитель ν(t) находится следующим образом:
 (1.10.11)
(1.10.11)
F(t) и ν(t) являются непрерывными функциями времени t когда δ(t) интегрируема. В том случае, если интенсивность процентов является постоянной величиной, т.е. δ(t) = δ для всех t, то множитель наращения и дисконтный множитель имеют вид F(t) = eδt и ν(t) = e–δt и используются в формулах (1.7.1) и (1.8.1).
В случае непрерывного начисления процентов наращенная сумма долга в момент t может быть найдена по формуле:
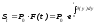 (1.10.12)
(1.10.12)
Если δ(t) представляет собой линейную функцию, т.е. δ(t) = δ0 + at, то
 (1.10.13)
(1.10.13)
где a – прирост силы роста.
Если δ(t) изменяется по параболе, т.е. δ(t) = δ0 + at + bt2, то
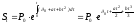 (1.10.14)
(1.10.14)
Современная стоимость суммы St, подлежащей выплате в момент t, равна
 . (1.10.15)
. (1.10.15)
где P0 - первоначальная сумма долга в момент t = 0.
◄ Пример.
Определить современную стоимость суммы 70 000 руб., выплачиваемой через 3,6 года, при линейном изменении силы роста. Начальное значение силы роста δ0 = 0,1, прирост силы роста a = 0,06.
|
Дано: Sn = 70 000 руб. t = 3,6 года δ0 = 0,1 a = 0,06 |
Решение:
|
Рассмотрим интегрируемую кусочно-постоянную функцию:
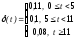
Найдем множитель наращения F(t). Если 0 t < 5, то
 .
.
Если 5 t < 11, то
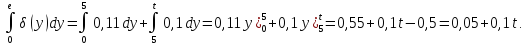
Если t 11, то
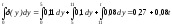 .
.
Таким образом,
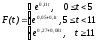 .
.
Рис. 1.1.9
Пусть, время
измеряется в годах. Найдем наращенную
сумму вклада 200 д.е., произведенного в
момент t
= 0, через 5 лет и через 13 лет. По
полученной формуле можем найти
St = P0 F(t)
= P0 e0,05+0,1·t,
если срок долга 5 t < 11,
и St = P0 F(t)
= P0 e0,27+0,08·t,
при t 11.
Тогда S5 = 200 e0,05+0,1·5 = 200 e0,55 = 346,65,
д.е. и S13 = 200 e0,27+0,08·13 =
= 200 e1,31 = 741,23,
(д.е.).



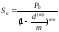
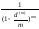
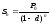
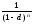



 =
=
33 105,36 руб.
=
=
33 105,36 руб.