4.3. Работа идеального газа при изопроцессах

Вычислим работу идеального газа при различных изопроцессах в соответствии с её определением

А=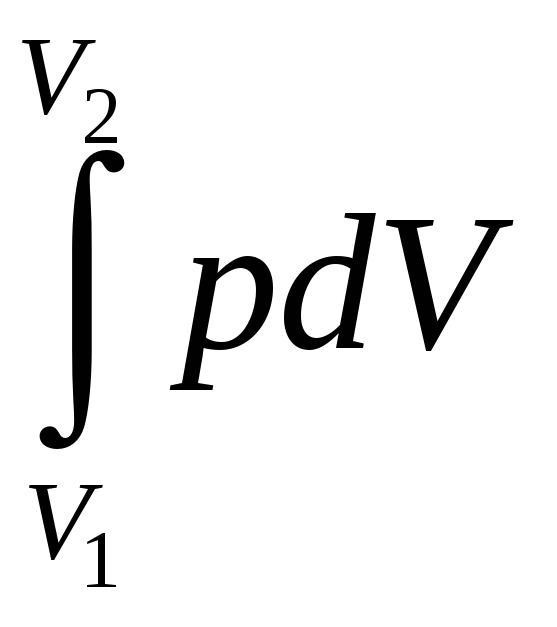. (5)

1. Изотермический процесс.

Подставив в (5) выражение р из уравнения pV=νRT₀, получаем:

.

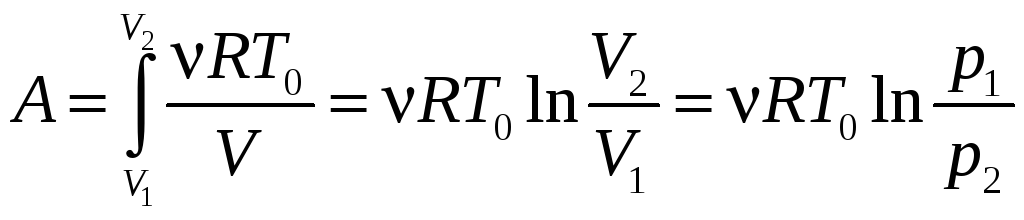2. Изохорный процесс. Так как здесь V=const, то А=0.

3. Изобарный процесс. Так как здесь р=const=р₀, то .

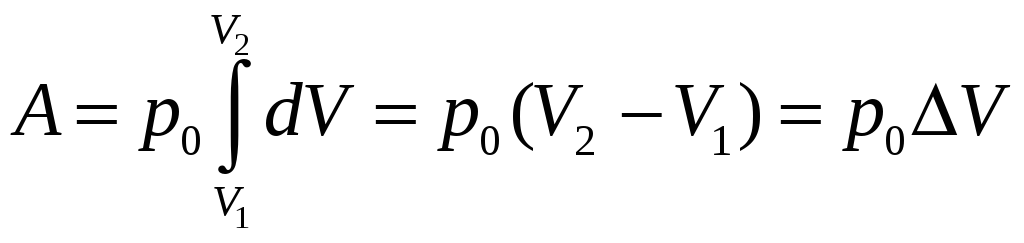4. Адиабатный процесс.

Так как здесь Q=0. то работа газа совершается только за счёт его внутренней энергии:

А=Q−ΔU=−ΔU=−νC_VΔT=νC_V(Т₁−Т₂). (6)

Отсюда видно, что при адиабатном расширении, когда А=pΔV>0, газ охлаждается, т.е. ΔТ<0.

Если в формулу (6) подставить Т₂ из уравнения адиабаты T₁V₁^γ−1=T₂V₂^γ−1, то получим ещё одно выражение для работы газа при адиабатном процессе:

А=νС_VТ₁(1−(V₁/V₂)^γ−1) (получить самостоятельно).

4.4. Адиабатный процесс в тропосфере

Известно, что температура тропосферы с высотой уменьшается. Основной причиной этого являются конвективные потоки воздуха, которые перемещают его из нижних слоёв тропосферы в верхние, и наоборот. Когда воздух с уровня моря поднимается в верхние слои с низким давлением, он расширяется. А так как воздух – плохой проводник тепла, то можно считать. что процесс расширения является адиабатным, что и приводит к понижению температуры. При потоке воздуха сверху вниз происходит его адиабатное сжатие, и температура повышается.

Вычислим в рамках этой модели изменение температуры с высотой. Для этого рассмотрим вертикальный столб воздуха сечением S и вырежем в нём тонкий слой dh на высоте h над уровнем моря (рис. 8). Масса воздуха в этом слое

dm=ρ(h)dV=ρSdh,

где ρ(h) – плотность воздуха на высоте h.Вес этого слоя воздуха dP=ρgSdh. Следовательно, уменьшение (убыль) давления с высотой – это давление этого слоя:

−dp=dP/S=ρgdh.

Плотность воздуха ρ выразим из уравнения состояния идеального газа pV=: ρ=. И тогда ,

или 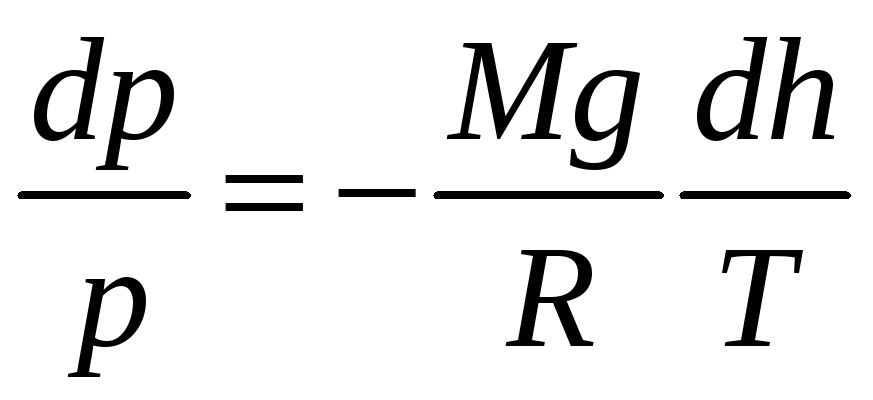. (7)

Выразим теперь левую часть (7) через Т. Для этого продифференцируем уравнение адиабаты (4):

d(.

Это даёт:

.

А так как 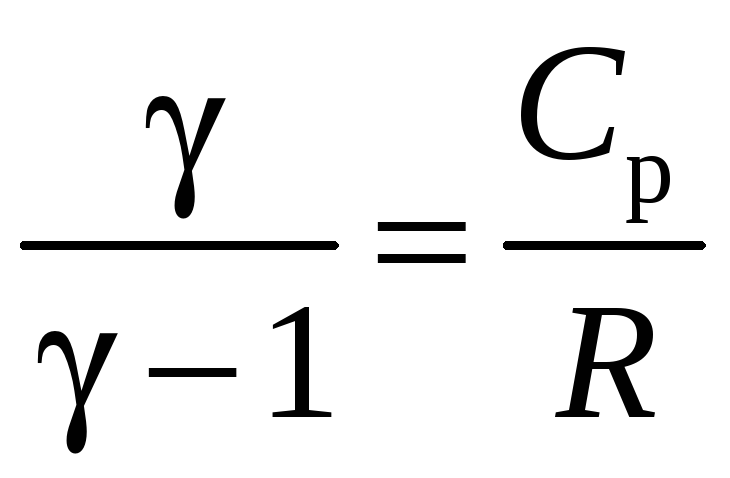, то .

И тогда (7) принимает вид:

С_рdT=−Mgdh,

или

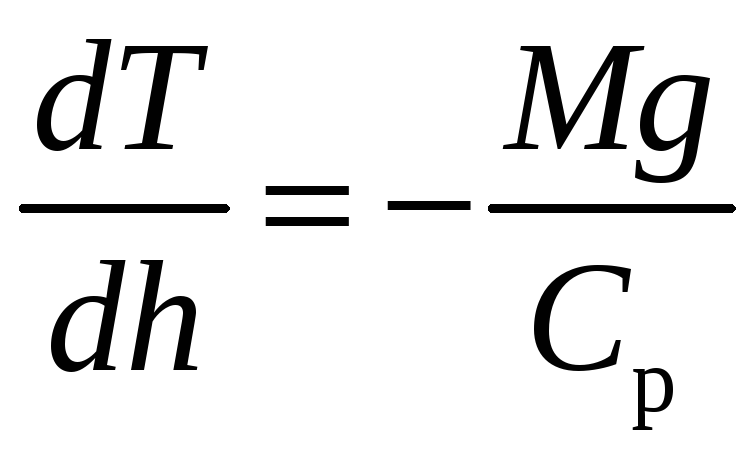. (8)

Подставляя сюда численные значения: g=9,8, М=0,029, С_р=(7/2)R=29, получаем искомое изменение температуры с высотой:

.

Реально температура воздуха снижается немного медленнее, так как в данной адиабатной модели атмосферы не учитывается эффект выделения тепла при конденсации водяного пара в расширяющемся, а следовательно, и охлаждающемся потоке воздуха.

4.5. Изотермическая модель атмосферы

Вернёмся к уравнению (7). Если в первом приближении полагать, что температура воздуха с высотой не меняется, т.е. считать, что Т=const (изотермическое приближение), то уравнение (7) легко интегрируется:

.

Постоянная интегрирования А определяется из условия: при h=0 давление р=р₀=1 атм. Это даёт: h=lnр₀. И тогда

. (9)

Эта формула называется барометрической и описывает изменение давления с высотой в изотермической модели атмосферы. Подстановка в (9) численных значений (М=0,029, g=9,8, R=8,31, Т=300) даёт, что давление атмосферы падает примерно в 2 раза на каждые 6 км высоты. График функции (9) показан на рис. 9.

Замечание. Если функцию Т(h) брать из адиабатной модели атмосферы, т.е. из (8), то уравнение (7) также легко интегрируется, но зависимость р(h) в этом случае будет более громоздкой.

Пример. Вычислить давление на вершине Эвереста в изотермическом приближении.

Решение. Полагая h=9000 м, М=0,029, Т=250 К (−23°С), из (9) получаем:

р=р₀е^−1,28≈0,28р₀.