Численное интегрирование

Путь на отрезке ab задана функция одной переменной. [a;b] y=f(x) . x0,x1,x2,..,xn Разобьем отрезом ab на n элементарных отрезков [xi-1;xi],i=1,n . x0=a xn=b. На каждом из этих элементарных отрезков выберем произвольную точку ξi и найдет произведение Si=f(ξi)∆xi.

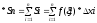Sn – называется интегральной суммой. Определенным интегралом f(x) на отрезке ab называется предел интегральной суммы при неограниченном увеличении числа точек разбиения.(интеграл)

Теорема существования определенного интеграла: Если функция f(x) непрерывна на отрезке ab. То предел интегральной суммы существует и не зависит не от способа разбиение отрезка, ни от точек разбиения ξi

ξ1x1

ξ2x2

ξ3x3

ξ4x4

Площадь полученной фигуры является интегральной суммой.

При неограниченном увеличении числа точек деления, т.е. при стремлении в 0 всех точек xi. Верхняя граница фигуры переходит в линии y=f(x). Площадь полученной фигуры называется площадью прямолинейной трапеции, она равна определенному интегралу. 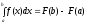На практике часто не имеет выражения уравненияf(x).

Если не имеем аналитическое выражение f(x) или нельзя выразить в численных функциях, то используем формулу чистого интегрирования т.е. дают приближенное значение интеграла с заданной точностью ε.

Общий подход к решению задач: Определённый интеграл I представляет собой S ограниченной кривой осью х и прямыми x=a x=b. Будем вычислять интеграл разбивая на множество мелких интегралов находя приблизительные площади полоски и складывая их.

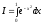
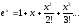
Методы численного интегрирования.

Метод прямоугольника. Интегральной суммой *, но в качестве точек ξi можно выбирать левые границы, или правые границы узлов отрезков.

h=∆xi=const

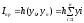
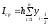
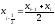
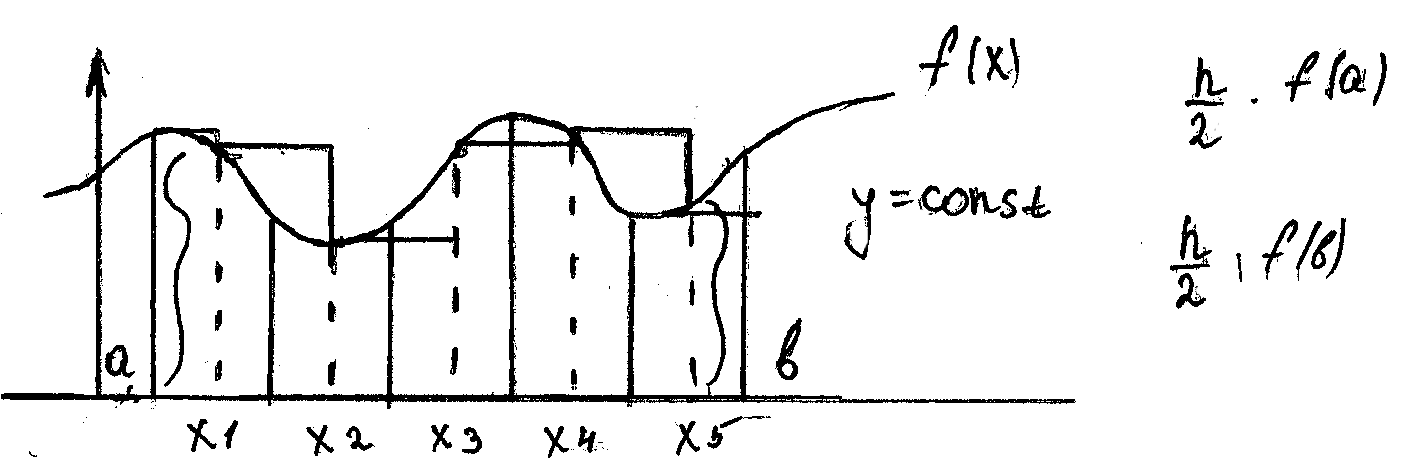
Более точные значения дают формулы если использовать средние точки для разбиения отрезка. Метод средних или метод прямоугольника в полуцелых узлах.

? в целых узлах.

Метод трапеций. Использует линейную интерполяцию для замены по интегральной функции.

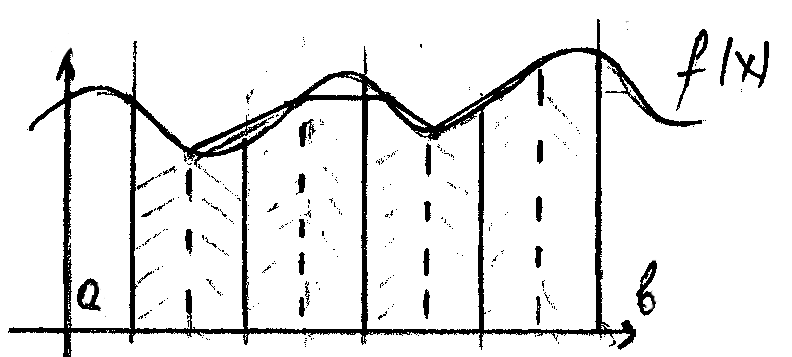
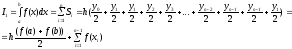На точность численного интегрирования влияет и порядок границы узлов и выбор точек разбиения.

Function F(x:real):real

F:=exp(-x*x);

a0=x

Конец

Начало

Ввод a,b,n

S=0 x=a h=(b-a)/n

a0=x

x<b

i=(F(a)+F(b))(2+s)*h

x=x+h s=S+F(x)

Конец

Для вычисления интеграла с заданной точностью ε рассмотрим алгоритм автоматического выбора шага. Шаг вычисляется при заданном начальным числом разбиения. Далее шаг должен корректироваться, а точность вычисления повышаться. Шаг здесь уменьшают на 2 раза и сравнивают 2 ближайших значения интеграла между собой. |I2-I1|<=ε

Начало

Ввод a,b,n,ε

I1=0 h=(b-a)/n

I2=Int(h,a,b)

|I2-I1|<=ε

Выв I2

H=h/2 I1=I2

Конец

Метод Симпсона

Метод Симпсона или парабол используют интерполяцию второго порядка квадратичную. В методе Симпсона разбиение четное, потому что парабола строится на 3х точках.

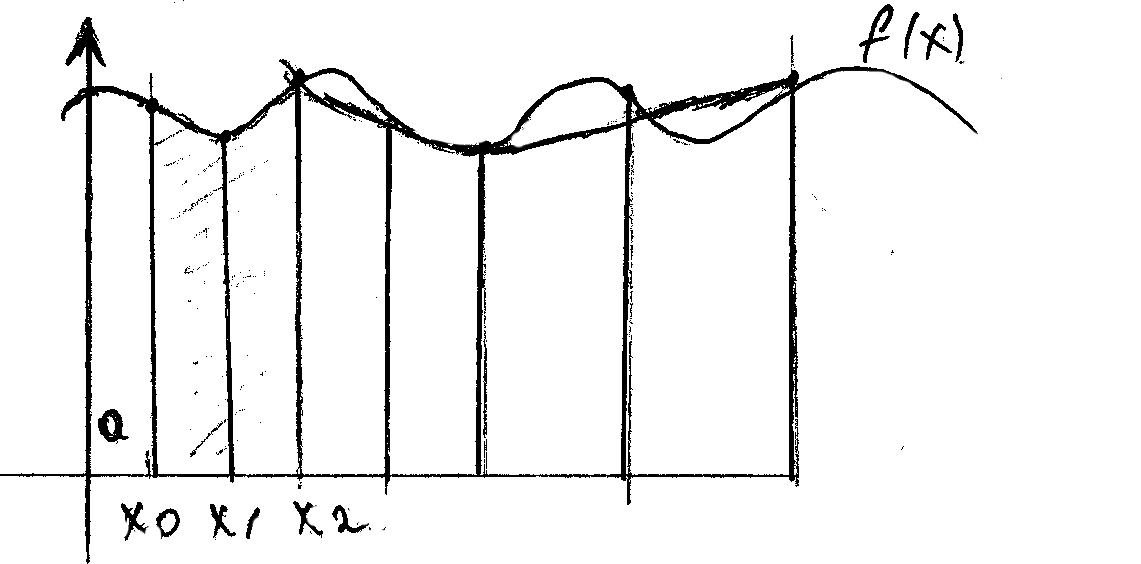В методе Симпсона вместо явной параболы неявное представление по Лагранжу.

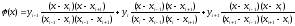
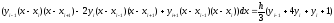
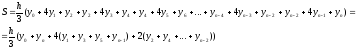
Function int(h,a,b;real):real;

x=a+h

s1=0 s2=0

X<b

Int=h/3*(F(a)+F(b)+4*S1+2*(s2-F(x-h))

S1=s1+F(x) x=x+h s2=s2+F(x) x=x+h

Конец

Решение систем линейный алгебраических уравнений

=

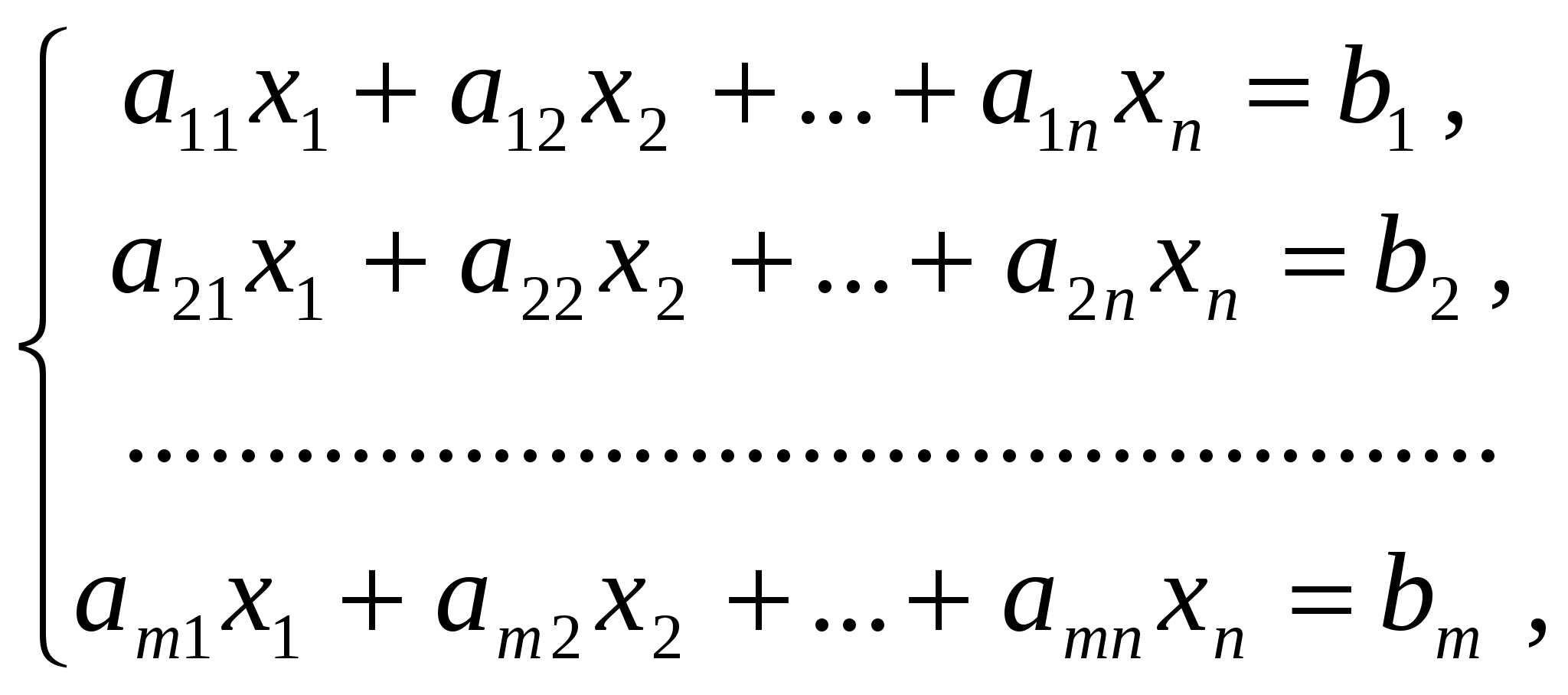
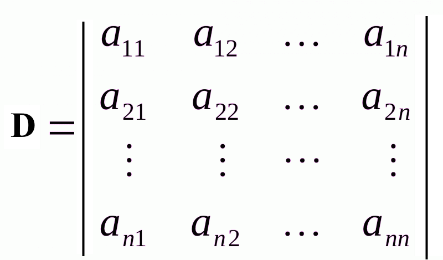
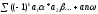
K число инверсий каждой перестановки. Необходимое и достаточное условие D<>0 . если D=0 вырожденная.

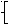С точки зрения практических вычислений могут существовать почти вырожденные системы. При решении которых можно получить недостоверные значения неизвестных. Такие методы решаются только итерационными методами. 5x+7y=12 7x+10y=17

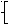X=1 y=1

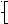Рассмотрим пару неизвестных x=2,415; y=0

5х+7у=12.075 7х+10у=16.905

После округление до 2х значащих цифр в правой части равенств совпадают с исходными. А т.к. исходные уравнения ?.

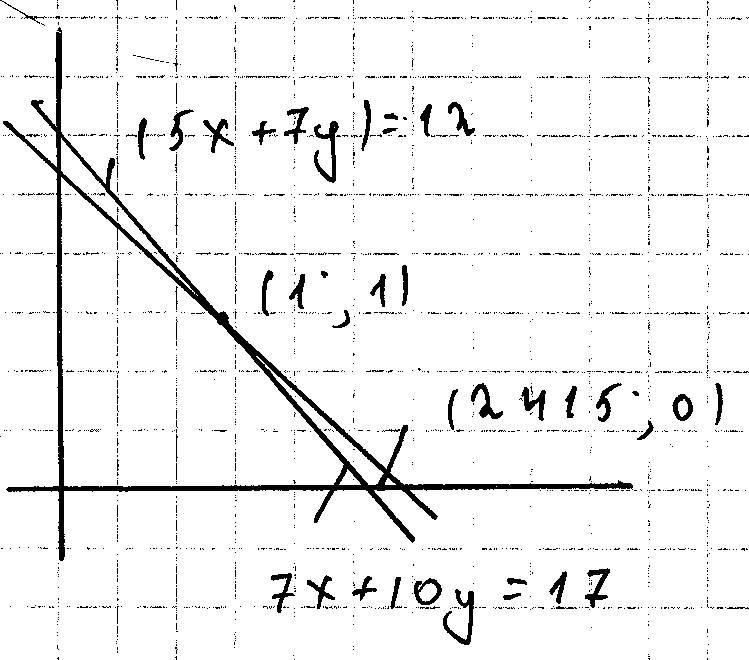
Дело в том, что 2 прямые линии. Они почти параллельны. Точка с (2 415;0) не лежит на них, но очень близка к ним. Системы такого типа называются плохо обусловленными, но матрицы таких систем почти вырождены.

Прямые методы применяются для порядка 30. Применяем в этом случае итерационные методов методы приближений. В интеграционных методах задаем начальное приближение. Затем с помощью некоторого алгоритма проводим цикл вычислений, называемый итерацией. В результате находим новое приближение. Проводим до получения решения с требуемой точностью.

Преимущества итерационных:

1. Не накапливают погрешности округлений, а корректирует их на каждой операции

2. Не требует одновременного хранения всей матрицы системы.

Недостаток:

Сходимость операций может быть медленной, или может разойтись вообще. Для безопасности разрабатывают условия сходимости.

Часто используют комбинацию методов, т.е. итерационные методы используют для уточнения решения полученных с помощью кривых.

Обратная матрица: A*A^-1=1

Прямые методы:

Метод гаусса – основан на приведении матрицы системы к треугольному виду, это достигается последовательным исключением неизвестных из системы.

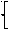A11+a12x2=a13x3=b1 0+     a22x2+a23x3=b2 0+     0+       a33x3=b3

Получаем ?. Затем идет обратных ход. Из последнего находим xn. Последним находится x1 из 1-го. К треугольному виду приводится невырожденная матрица.

Для адекватной реализации формулировки нужна безопасность расчётов?. Поэтому метод гаусса программируется вместе с алгоритмом поиска ?.

(Где 2 строка с ')

В Процессе исключение неизвестных придется делить на диагональные коэф. Поэтому они должны быть отличными от нуля. Иначе необходимо соответствующим образом переставить уравнения местами при перестановке меняем знак на противоположный. Соответствующий программный алгоритм называется поиском не нулевого ведущего элемента (диагональный). Обратный ход начинается с решения 3го уравнения

Х3=b3’’/a3’’

X2=1/a22’=(b2’-a23’x3)

X1=1/a11(b1-a12x2-a13x3)

Обобщим метод на систему n-го порядка. Пусть а11=0. Введем n-1 множители. Вычтем из каждого i го уравнение первое до множенное на ci. ci=ai1/a11 aij=aij-ci*a1j (i=2 to n) bi=bi-ci*b1 ai-1=0

Дальше убеждаемся в том, что для всех уравнений начиная со 2-го ai1=0. Таким же образом для исключения х2 из всех уравнений ниже второго, затем х3 исключаем подобным образом из всех уравнений ниже 3-го и тд. На некоторым k этапе мы исключаем xk с помощью множителей, которые вычисляются следующим образом.

(-x2) (I=3 to n)

Ci^(k-1)=aik^(k-1)/akk ^(k-1) i=((k+1) to n)

a^(k-1)kk <>0

aij ^(k)=aij^(k-1)-cj^(k-1)-akj^(k-1) i=(k+1) to n j=k to n

Bi (^k)=bi^(k-1)-ci^(k-1)-bk^(k-1) k=1 to (n-1)

Происходит исключение x_n-1 из последнего уравнения. Окончательная треугольная система имеет следующий вид.

Обратный ход для нахождения неизвестных задается следующими формулами.

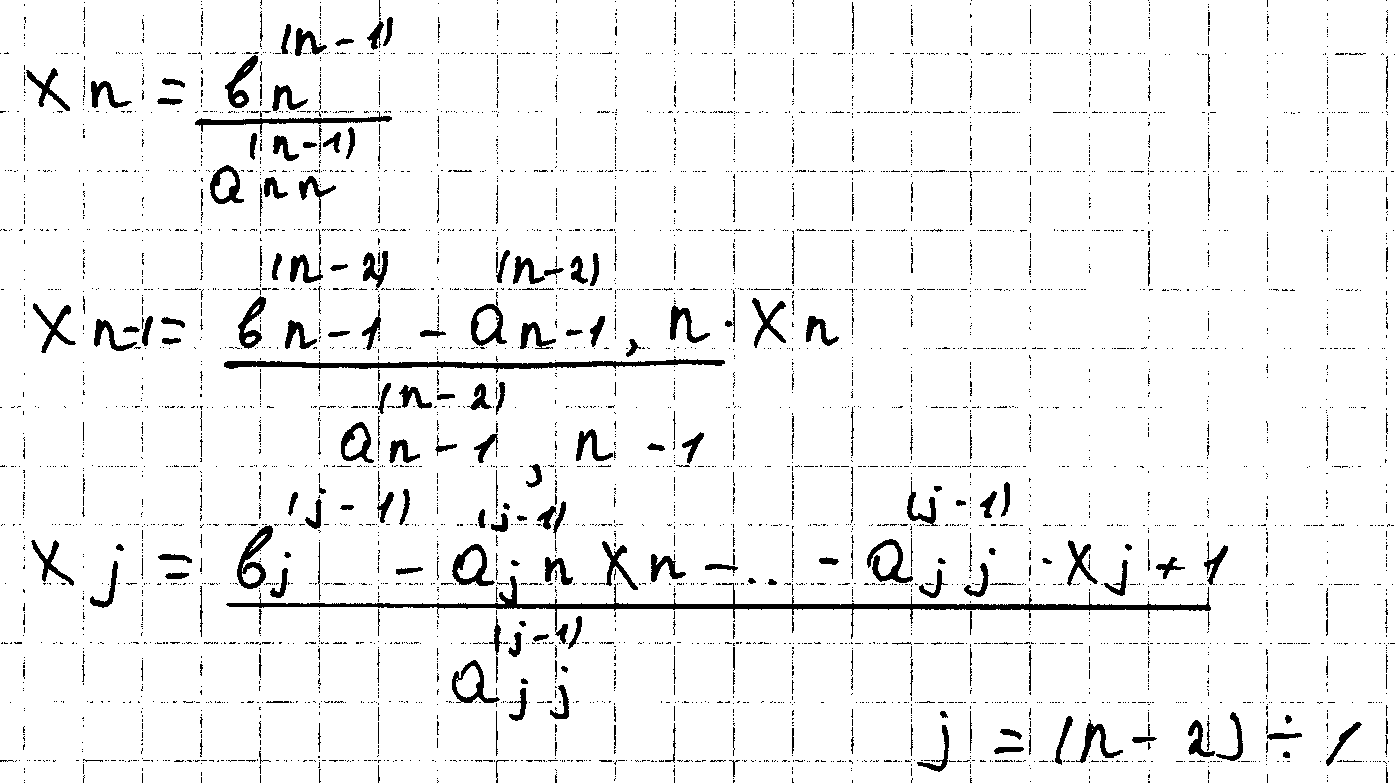
Блок схема метода гаусса с поиском ведущего не нулевого элемента. Будем использовать расширенную матрицу коэффициентов в которой вектор правых частей введен как правый столбец.

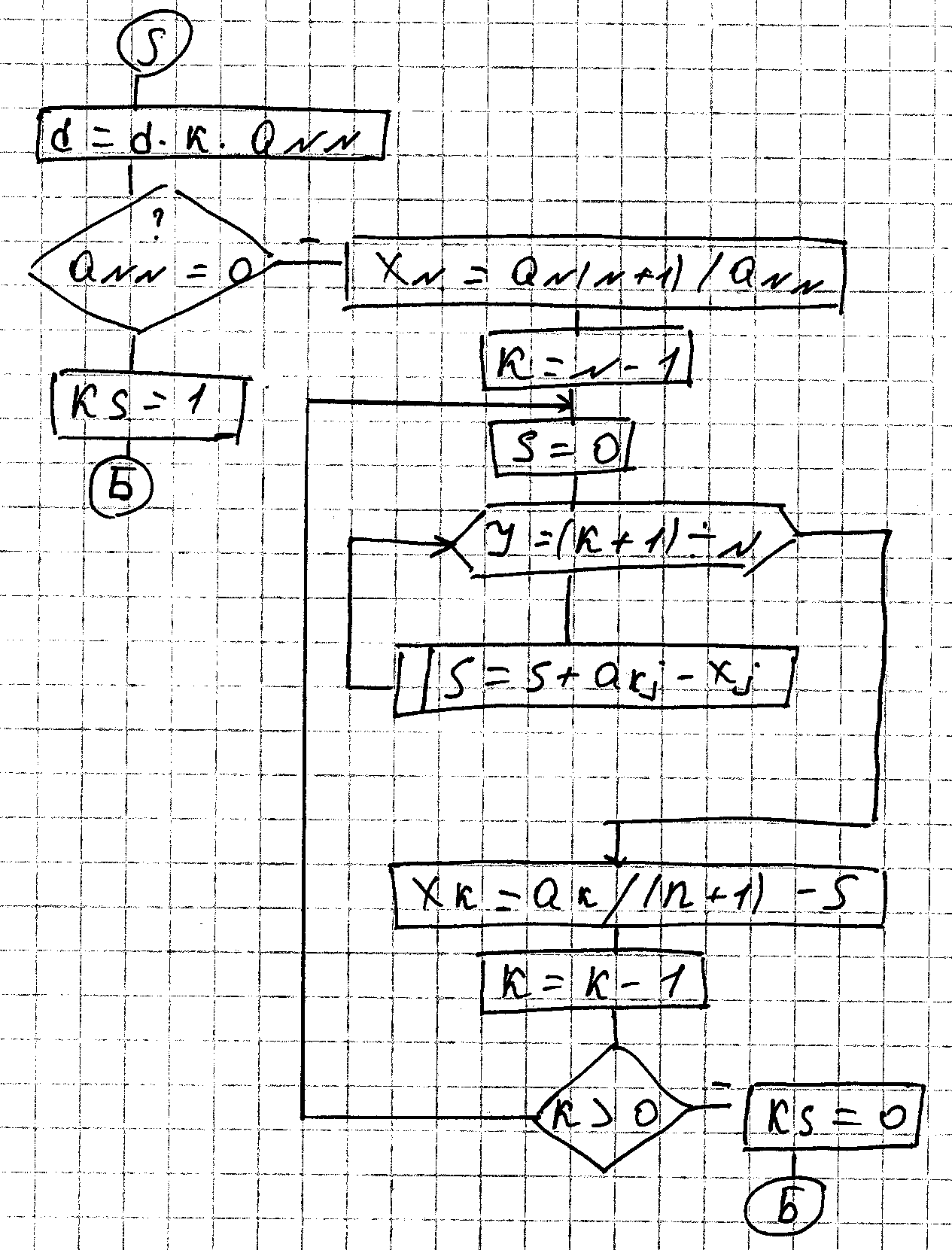
Поиск ненулевого ведущего элемента

if a[I,j]=0 then begin for M=1 to N do begin if a[M,i]=0 then continue else begin ks=0; goto l; end; l:for j=I to (n+1)do begin w=a[I,j] a[I,j]=a[m,j] a[m,j]=w; end; end else …

Схема с выбором главного элемента. Они состоит в том, что требования неравенства 0 главного элемента заменяется более жестким: из всех оставшихся в k стобце элементов нужно выбрать наибольший по модулю. И переставить уравнение так, чтобы найденный элемент оказался на месте ak.

Вычисление определителя и нахождение обратной матрицы с использованием метода гаусса.

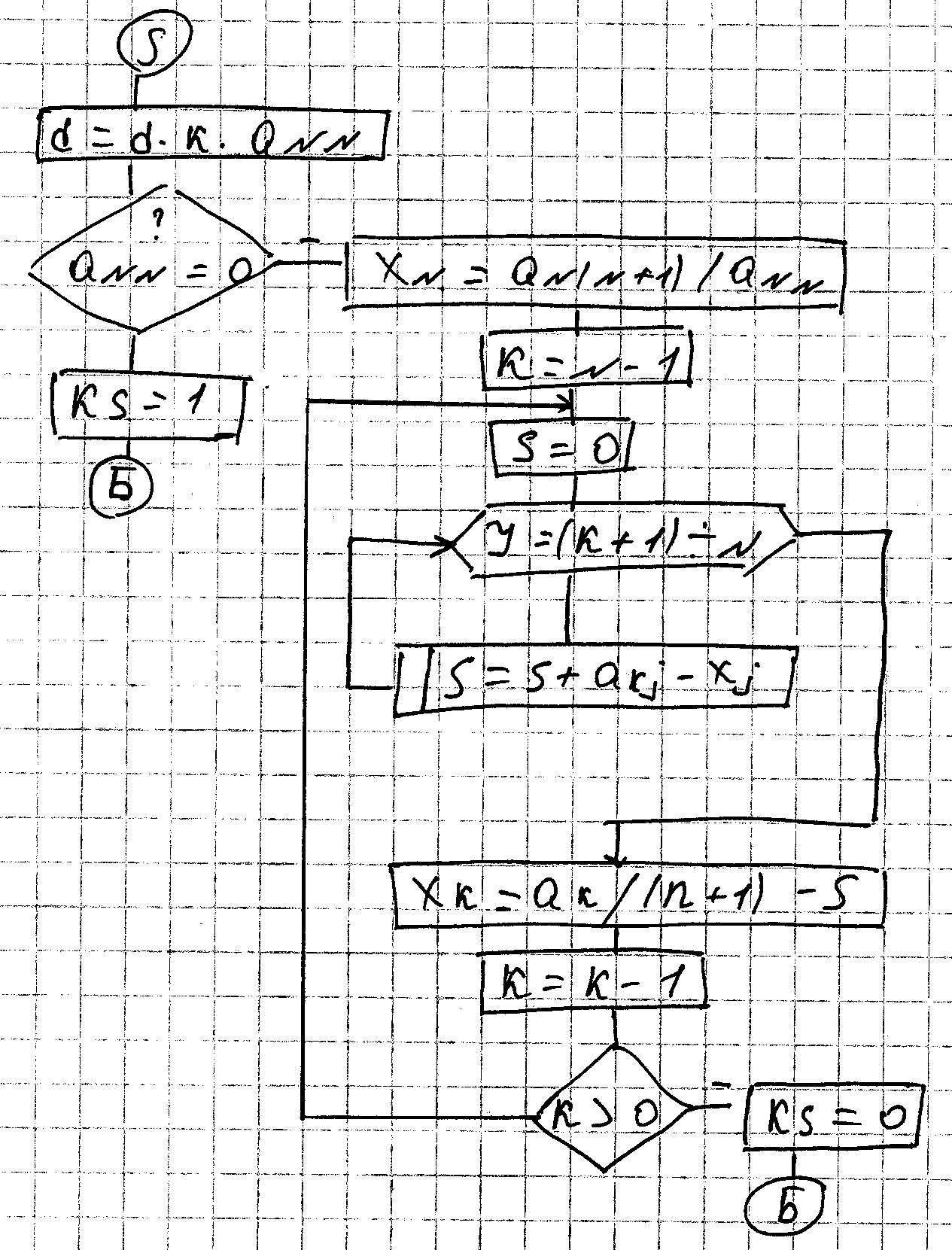
Легко вычисляется определитель треугольной матрицы, он равен произведению ее диагональных элементов. Для приведение матрицы к треугольному методу используем прямой ход метода гаусса. Знак меняется на противоположный при перестановке строк или столбцов. Следовательно, следует учесть знак в поиске ненулевого ведущего элемента.

D=d*a*k*aNN

Обратную матрицу найдем из A*A^-1=E

Пр.

Для нахождения элементов одного столбца обратной матрицы необходимо решить линейную систему с исходной матрицей коэффициентов А расширенной на всю матрицу Е по правым частям. Прямой ход метода гаусса для получения треугольной матрицы исходные коэффициенты проводим один раз, но с учетом того, что справа стоит вся единичная. Обратных ход идет n раз для нахождения элементов j столбца обратной матрицы выбирается j столбец из преобразованных правых частей единичной матрицы.