Глава 2
Аппроксимация с гарантированной точностью
2.1Алгоритмы с оценками точности
Приближенные алгоритмы с оценками точности. Жадные алгоритмы для задач типа покрытия и упаковки. Приближенные алгоритмы на графах.
Одним из общих подходов к решению NP-трудных задач, который активно развивается в настоящее
70
2.1. АЛГОРИТМЫ С ОЦЕНКАМИ ТОЧНОСТИ |
71 |
время, является разработка приближенных алгоритмов с гарантированными оценками качества получаемого решения.
Точность приближенного алгоритма характеризует мультипликативная ошибка, которая показывает, в какое максимально возможное число раз может отличаться полученное решение от оптимального (по значению заданной целевой функции).
Определение 2.1.1. Алгоритм называется C-приближенным, если при любых исходных данных он находит допустимое решение со значением целевой функции, отличающимся от оптимума не более чем в C раз.
Заметим, что иногда также говорят об C1 -приближенных алгоритмах, причем смысл отклонения (больше или меньше единицы) обычно ясен из контекста и направления оптимизации (максимизации или минимизации). Мультипликативная ошибка может быть константой или зависеть от параметров входной задачи. Наиболее удачные приближенные алгоритмы позволяют задавать точность своей работы. В качестве примера перечислим приближенные алгоритмы, которые мы рассмотрим далее в этой книге:
•2-приближенный алгоритм для задачи о рюкзаке из раздела 2.1.3.
•3/2-приближенный алгоритм для метрической задачи коммивояжера из раздела 2.1.4.
•0; 878-приближенный алгоритм для задачи о максимальном разрезе в графе из раздела 4.4.2.
•2-приближенный алгоритм для минимального вершинного покрытия из раздела 2.1.2.
•(1 + ln m)-приближенный алгоритм для задачи о покрытии из раздела 2.1.1.
•(1 + ")-приближенный алгоритм для задачи о рюкзаке из раздела 2.2.2.
72 |
Глава 2. АППРОКСИМАЦИЯ С ГАРАНТИРОВАННОЙ ТОЧНОСТЬЮ |
2.1.1Жадные алгоритмы для «Покрытия множеств»
Жадные алгоритмы для задачи о покрытии подмножеств, локальный алгоритм для вершинного покрытия.
Одной из простейших эвристик, часто применяемых при решении различных задач, является так называемая жадная эвристика. Для некоторых задач, например, для задачи об остовном дереве минимального веса в графе, эта эвристика фактически позволяет найти оптимальное решение (см. алгоритм 9 «MST Прима»). В более трудных случаях она позволяет получать гарантированные оценки точности получаемого с ее помощью решения.
Рассмотрим сейчас жадную эвристику для классической NP-трудной задачи — задачи о покрытии.
Задача 10. «Покрытие множества»¹.
•Множество X, jXj = m.
•Семейство подмножеств fS1; : : : ; Sng, Sj X.
•X = [nj=1Sj (покрытие гарантировано).
¹В англоязычной литературе — Set Cover.
2.1. АЛГОРИТМЫ С ОЦЕНКАМИ ТОЧНОСТИ |
73 |
Найти минимальное по мощности множество подмножеств, покрывающее X:
jJj ! min;
J f1; 2; : : : ; ng;
X = [j2J Sj:
Число jJj называется размером минимального покрытия.
Известно, что задача о покрытии NP-полна. По этой причине трудно надеяться на существование полиномиального алгоритма точного ее решения.
Рассмотрим алгоритм 15, который действует в соответствии с простейшей жадной эвристикой: «На каждом шаге выбирать максимально непокрытое подмножество», т. е. подмножество, содержащее максимальное число элементов, не покрытых на предыдущих шагах. Далее мы оценим гарантируемую им точность.
Теорема 1. Алгоритм 15 гарантирует точность 1 + ln m для задачи 10 «Set Cover».
Доказательство. Пусть,
Xk — число непокрытых элементов после k-го шага.
M = jJj — размер минимального покрытия.
Так как на любом шаге k, Xk непокрытых элементов мы можем «накрыть» минимальным покрытием размера M, при этом обязательно будет подмножество, которое накроет XMk непокрытых элементов (иначе будет противоречие — минимальное покрытие не сможет накрыть Xk непокрытых элементов, и, следовательно, и полное множество тоже). Значит, жадный алгоритм на k-м шаге накроет не менее XMk непокрытых элементов, и получится
74 |
Глава 2. АППРОКСИМАЦИЯ С ГАРАНТИРОВАННОЙ ТОЧНОСТЬЮ |
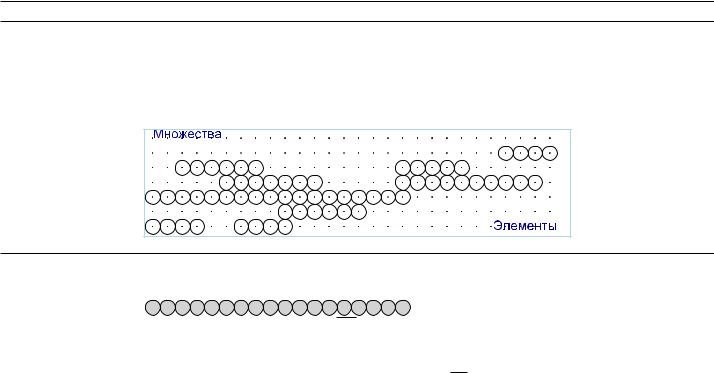
Алгоритм 15 Жадный алгоритм для задачи о покрытии
«Каждый раз выбирать максимально непокрытое подмножество».
На рисунке столбцы соответствуют элементам множества, строки — подмножествам. т. е. каждый графический объект с координатами x; y представляет принадлежность некоторого элемента x подмножеству y. Показаны фазы работы жадного алгоритма — темным цветом выделены выбранные алгоритмом подмножества.
Xk+1 Xk |
Xk |
= Xk(1 1/M): |
(2.1) |
|
M |
||||
Xk m(1 1/M)k m exp ( |
k |
|
||
M ) : |
|
|||
Найдем наибольшее k0, при котором m exp |
k0 |
1. |
|
|
M |
|
|
||
( )
Тогда при k1 = k0 + 1 выполнено Xk1 < 1, что означает, что все элементы покрыты. При этом k1/M 1 + ln m, значит, размер покрытия, построенного жадным алгоритмом, превосходит минимальное не более чем в 1 + ln m раз. 
2.1. АЛГОРИТМЫ С ОЦЕНКАМИ ТОЧНОСТИ |
75 |
Упражнение 2.1.1. Докажите неравенство (2.1).
Упражнение 2.1.2. Постройте пример, где оценка O(1 + ln m) мультипликативной ошибки жадного алгоритма достигается по порядку. Указание: достаточно рассмотреть случай, когда размер минимального покрытия M = 2.
Упражнение 2.1.3. Постройте пример, где оценка 1 + ln m достигается асимптотически.
Встречаются и другие оценки точности жадного алгоритма. Доказано, например (см. [Joh73]), что мультипликативная ошибка жадного алгоритма не превосходит
1 + 12 + 13 + : : : + m1 :
Асимптотически это выражение как раз равно ln m. Более точная оценка получена в [Sla96], где доказано, что мультипликативная ошибка жадного алгоритма не превосходит ln m ln ln m + O(1).
Возникает законный вопрос: а насколько хороши полученные оценки? Достижимость оценки означает лишь, что мы достаточно точно оценили ошибку жадного алгоритма. Однако вполне возможно существование других полиномиальных алгоритмов с лучшими оценками. Вопрос этот на самом деле является непростым, и только относительно недавно на него удалось дать удовлетворительный ответ [Fei98].
Оказалось, что при разумных теоретико-сложностных предположениях, а именно NP ̸ DT IME(nO(log log n))², никакой полиномиальный алгоритм для задачи о покрытии не может иметь мультипликативную ошибку меньше (1 ) ln m для любого фиксированного > 0.
Все это является следствием так называемой PCP-теоремы и ее связями с неаппроксимируемостью (см. теорему 37).
²См. определения 6.2.4 на стр. 259 и 6.1.7 на стр. 250.
76 |
Глава 2. АППРОКСИМАЦИЯ С ГАРАНТИРОВАННОЙ ТОЧНОСТЬЮ |
Но, с другой стороны, существует ряд классических разновидностей задачи о покрытии с лучшими оценками аппроксимации. Например, «максимизационный» вариант задачи 10 «Set Cover».
Задача 11. «K-покрытие» Задано:
•Множество X, jXj = m.
•Семейство подмножеств fS1; : : : ; Sng, Sj X.
Выбрать такие k подмножеств, чтобы мощность их объединения была максимальна:
j [j2J Sjj ! max; J f1; 2; : : : ; ng;
jJj = k:
Оказалось, жадный алгоритм дает хорошие результаты и для этой задачи.
Теорема 2. Жадный алгоритм 15 является (1 e 1)-приближенным алгоритмом для задачи 11 «К- покрытие».
Доказательство. Пусть Yi обозначает число покрытых элементов после i-го шага жадного алгоритма, а M — оптимум в задаче о k-покрытии. Справедливо следующее неравенство (см. упражнение 2.1.1):
( )
Yi+1 Yi + |
M |
Yi |
= |
M |
+ Yi |
1 |
1 |
: |
|
k |
k |
k |