Совместность однородной системы

 

Рассмотрим однородную систему

.

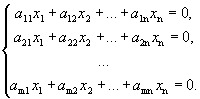Однородная система всегда совместна, так как всегда имеет тривиальное (нулевое) решение . Выясним, когда данная система имеет нетривиальное решение.

Теорема 1. Однородная система имеет нетривиальное решение тогда и только тогда, когда ранг матрицы, составленной из коэффициентов при неизвестных, меньше числа неизвестных.

Доказательство. Пусть система совместна. Это может быть тогда и только тогда, когда найдутся числа с₁, с₂, …, с_n, при подстановке которых в систему мы получим mтождеств. Эти m тождеств можно записать в виде

.

Следовательно, система векторов-столбцов матрицы А линейно зависима. А это может быть тогда и только тогда, когда ранг системы векторов-столбцов меньше n, т.е. r(A)<n.

Следствие. Квадратная однородная система имеет нетривиальное решение тогда и только тогда, когда определитель матрицы, составленной из коэффициентов при неизвестных, равен нулю.

Доказательство. Так как r(A)<n, то столбцы матрицы линейно зависимы и, следовательно, определитель матрицы равен нулю.

№17

Основные определения.

Пусть К – поле. Элементы поля К мы будем называть скалярами. Под полем К можно понимать или поле действительных чисел или поле комплексных чисел.

Определение. Матрицей размера  над полем К называется таблица элементов поля К, имеющую  строк и  столбцов.

Обозначение:

.

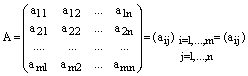Определение. Элементы  называются элементами матрицы, где  i – номер строки, в которой находится элемент , j – номер столбца.

Определение. Матрица размеров :

 называется строкой длины .

Определение. Матрица размеров :

 называется столбцом высоты .

Определение. Матрица размеров  называется квадратной матрицей – го порядка.

Определение. Матрица, все элементы которой равны нулю, называется нулевой.

В квадратной матрице выделяют две диагонали, как диагонали квадрата: главную диагональ и побочную диагональ.

Главную диагональ образуют элементы , т.е. элементы с одинаковыми нижними индексами.

Побочную диагональ образуют элементы .

Определение. Квадратная матрица, в которой все элементы вне главной диагонали равны 0, называется диагональной:

.

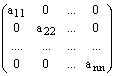Определение. Матрица В размера  называется транспонированной по отношению к матрице А размера , если к – й столбец матрицы В состоит из элементов к – й строки матрицы А, для всех.

Обозначение: .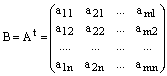

Определение. Процесс (процедура) получения транспонированной матрицы из данной называется транспонированием матрицы.

Пример:

, .

Определение. Две матрицы  и  называются равными, если они имеют одинаковые размеры и для всех значений индексов выполняется равенство .

Свойства опрераций над матрицами

A+B=B+A

(A+B)+C=A+(B+C)

λ(A+B)=λA+λB

A(B+C)=AB+AC

(A+B)C=AC+BC

λ(AB)=(λA)B=A(λB)

A(BC)=(AB)C

(A')'=A

(λA)'=λ(A)'

(A+B)'=A'+B'

(AB)'=B'A'

№18

Рангом системы строк (столбцов) матрицы  с  строк и  столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.

Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.

Обычно ранг матрицы  обозначается  ()

Элементарными преобразованиями строк называют:

• перестановка местами любых двух строк матрицы;

• умножение любой строки матрицы на константу , ;

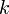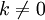• прибавление к любой строке матрицы другой строки.

В некоторых курсах линейной алгебры перестановка строк матрицы не выделяется в отдельное элементарное преобразование в силу того, что перестановку местами любых двух строк матрицы можно получить, используя умножение любой строки матрицы на константу ,  и прибавление к любой строке матрицы другой строки, умноженной на константу , .

Аналогично определяются элементарные преобразования столбцов.

Элементарные преобразования обратимы.

Обозначение  указывает на то, что матрица  может быть получена из  путём элементарных преобразований (или наоборот).

Вычисление ранга матрицы с помощью миноров

Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D k-го порядка матрицы А, отличный от нуля, то требуют вычисления лишь миноры (k+1)-го порядка, окаймляющие минор D, т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен k.

Пример 1. Найти методом окаймления миноров ранг матрицы

.

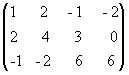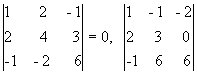Решение. Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) М₁ = 1, расположенный в первой строке и первом столбце. Окаймляя при помощи второй строки и третьего столбца, получаем минор M₂ = , отличный от нуля. Переходим теперь к минорам 3-го порядка, окаймляющим М₂. Их всего два (можно добавить второй столбец или четвертый). Вычисляем их:  = 0. Таким образом, все окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум.