
Nechepurenko_ФТИ
.pdf
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ОЦЕНКА ПОГРЕШНОСТИ |
|
|
|
|
|
|
|
|
|
408 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Пусть u |
Ll |
|
( |
|
|
|
|
|
, |
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(s) |
|
|
|
|
(s) |
~ |
(s) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(s) |
|
|
|
|
|
|
u(s) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
y(s) y(s) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
ˆ |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1/ 2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1/ 2 |
||||||||||||||
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
y(t) y(t) |
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(i |
|
|
|
ˆ |
|
|
|
|
|
|
d |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) y(i ) |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1/ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
max |
|
(i |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
u(i |
|
|
|
|
ˆ |
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) u (i ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1/ 2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
max |
|
) |
|
|
|
2 |
|
|
|
u(t) |
|
|
|
22 dt |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(i |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
max |
|
|
2 |
, |
{ 1, , N } |
|
|
(i ) |
|
||||
|
|
|
|
|
|
|

|
|
|
ВЫЧИСЛЕНИЕ БАЗИСА В |
409 |
||||
|
|
|
|
|||||
|
|
ПОДПРОСТРАНСТВЕ КРЫЛОВА |
|
|||||
U |
A 1C, |
M |
A 1B |
|
|
(m |
pk n) |
|
|
|
|
|
|
Cn m : |
|
||
Найти X |
[ X1,...,X p ] |
X X |
Im |
|
||||
|
spanX |
span |
U , MU , M 2U , , M k 1U |
|
||||
Ортогонализация Грама-Шмидта: |
|
|
|
|||||
X1 : ort (U ) |
|
|
|
|
|
|
||
w : |
MU , |
w : |
w |
X1( X1 w), X 2 : |
ort (w) |
|
||
X 2 |
X1 |
|
|
|
|
|
|
|
w : |
M 2U, |
w : |
w |
X1( X1 w), w : |
w |
X 2 ( X 2 w), X3 : |
ort(w) |
|
X3 |
X j , |
j 1,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и любая другая ортогонализация приведет к КАТАСТРОФИЧЕСКОЙ потере точности:
(span {U, MU, , M j 1U}, span {M jU}) exp( cj)

МЕТОД АРНОЛЬДИ |
410 |
|
X1 ort (U )
w : |
MX1, w : w |
X1( X1 w), X 2 : |
|
|
ort (w) |
|||||
X 2 |
span{X1, MX1}, X 2 |
X1 |
|
|
|
|
||||
w : |
MX2 , w : w |
X1( X1 w), w : |
w |
X 2 ( X 2 w), X3 : ort(w) |
||||||
X |
3 |
span{X |
, MX , M 2 X }, |
X |
3 |
X |
j |
, |
j 1,2 |
|
|
1 |
1 |
1 |
|
|
|
|
|||
(span {X1, X2 , , X j}, span {MX j})
(span {U, MU, , M j 1U}, span {M jU})

411
X1 ort (U ) for i 1, , k
w |
|
MXi |
|
|
|
|
|
|
|
|
|
|
|||||
for |
|
l |
1,2 |
|
|
|
|
|
|
|
|
|
|
||||
|
for |
j |
1, ,i |
|
|||||||||||||
|
|
|
|
w |
w X j ( X j w) |
|
|||||||||||
|
end |
|
|
|
|
|
|
|
|
|
|
||||||
end |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
if |
|
w |
|
|
|
2 |
tol |
|
|
|
MXi |
|
|
|
2 STOP |
||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||
Xi 1 ort(w)
end
ВЫЧИСЛИТЕЛЬНЫЕ ЗАТРАТЫ:
- ортогонализация с дефляцией, например, на основе сингулярного разложения:
G |
Zdiag ( 1 |
|
p )V |
F |
Z1, , Zl |
, l |
tol l 1 |
cnp2k 2 |
pk ( умножений M на вектор ) |

СБАЛАНСИРОВАННОЕ УСЕЧЕНИЕ |
501 |
|
X X1, , X m , Y
m
x(t)
n, p, q |
j 1 |
|
|
Y , ,Y , Y * X |
I |
m |
||
|
1 |
m |
|
|
|
~ |
(t) X j |
~ |
|
|
|
x j |
X x (t) |
m, p, q |
|||
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
~~ |
~ |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
dx |
|
||||
|
|
|
Ax |
Cu |
|
|
~ |
|
|
|
|
|
|
Ax |
Cu |
|
|
|
|
|
|
Y AX |
|
|
|
dt |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
dt |
|
|
|
|
A |
|
|
|
~ |
~~ |
|
|||
|
|
y |
Ox |
|
|
~ |
Y C |
|
|
|
|
|
|
|||
|
|
|
|
|
C |
|
|
|
|
|
y |
Ox |
|
|||
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
~ |
~ ~ |
|||||
H(s) O(sI A) 1C |
|
|
O OX |
|
||||||||||||
|
|
|
H (s) O(sI A) 1C |
|||||||||||||
|
|
|
|
|
|
|
|
~ |
~ |
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
ˆ |
|
y(s) |
H (s)u(s) |
|
|
||||||
|
|
|
y(s) |
H (s)u(s) |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
(s) |
~ |
(s) |
~ |
|
|
y(s) |
|
|
|
|||
|
|
|
|
|
|
y(s) |
|
|
|
|
|
|||||

|
СБАЛАНСИРОВАННОЕ УСЕЧЕНИЕ |
502 |
|||||||
|
|
||||||||
x(t ) |
x0 ; |
|
dx |
Ax |
Cu |
|
|
|
|
|
|
|
|
|
|
||||
0 |
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Формула Коши: |
|
|
t |
|
|
||||
|
|
|
|
|
|
|
|
|
|
x(t) |
exp{(t |
t0 ) A}x(t0 ) |
|
exp{(t s) A}Cu(s)ds |
|
||||
|
|
|
|
|
|
|
t0 |
|
|
Уравнение Ляпунова: |
A*P |
PA |
D |
|
|||||
Re ( A) |
0 |
|
решение |
, единственн о |
|
||||
и представим о в виде |
P |
exp{tA*}D exp{tA}dt |
|
||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
0 |
|
Доказатель ство : Z (t) exp(tA* )D exp(tA); |
dZ |
A*Z ZA |
|
dt |
|||
|
|

УПРАВЛЯЕМОСТЬ |
503 |
dx |
Ax Cu |
Re ( A) 0 |
|
|
|||
dt |
|||
|
|
ЗАДАЧА: Достичь заданное состояние x(0) с наименьшим по норме u(t) :
|
|
|
|
0 |
1/ 2 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
u(t) u(t)dt |
min, |
exp{ tA}Cu(t)dt |
x(0) |
||||
|
|
|
|
|||||||||
|
|
|
|
|
|
tA }P 1x(0), |
|
|
|
|
x(0) P 1x(0) 1/ 2 |
|
РЕШЕНИЕ: uopt (t) |
C exp{ |
|
|
|
||||||||
|
uopt |
|
|
|||||||||
P |
exp{tA}CC exp{tA }dt |
0 - ГРАМИАН управляемости |
||||||||||
0
AP PA CC
P – вырожденная в том и только том случае, если столбцы C принадлежат инвариантному подпространству матрицы A размерности < n.
Если P вырожденная, то есть состояния, достичь которые нельзя.
|
НАБЛЮДАЕМОСТЬ |
504 |
|
|
|
||
dx |
Ax, y Ox, t 0 |
Re (S) 0 |
|
|
|
||
dt |
|
||
|
|
|
|
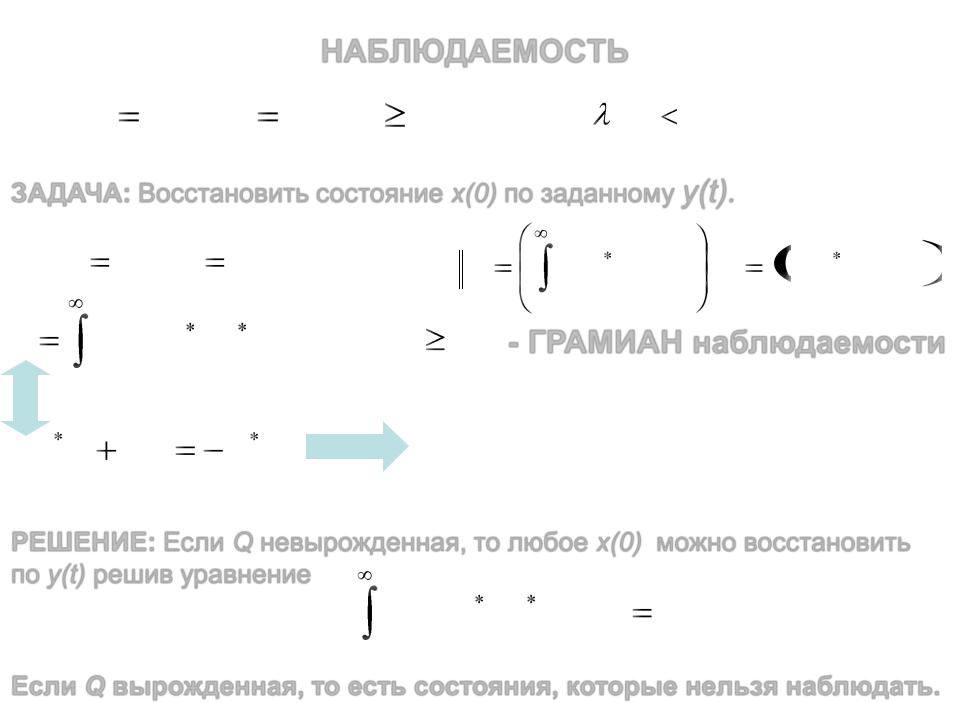
ЗАДАЧА: Восстановить состояние x(0) по заданному y(t).
y(t) Ox(t) O exp{tA}x(0)
Q exp{tA }O O exp{tA}dt
0
A Q QA O O
|
|
|
1/ 2 |
y |
|
y(t) y(t)dt |
x(0) Qx(0) 1/ 2 |
|
|||
|
|
|
|
|
|
0 |
|
0 - ГРАМИАН наблюдаемости
Q– вырожденная в том и только том случае, если столбцы O принадлежат инвариантному подпространству матрицы A размерности < n.
РЕШЕНИЕ: Если Q невырожденная, то любое x(0) можно восстановить по y(t) решив уравнение
exp{tA }O y(t)dt Qx(0).
0
Если Q вырожденная, то есть состояния, которые нельзя наблюдать.

СБАЛАНСИРОВАННОЕ УСЕЧЕНИЕ |
505 |
dx |
Ax |
Cu |
|
|
|||
dt |
|||
y |
Ox |
||
|
|
|
~ |
~ |
~ |
||
|
|
|
dx |
~~ |
||
|
x |
X x |
|
|
Ax |
Cu |
|
|
dt |
||||
|
~ |
Y AX |
|
~ |
~~ |
|
~ |
A |
|
|
|||
|
~ |
OX |
y |
Ox |
||
C Y C |
O |
|
|
|||
Если P почти вырождена, то есть состояния, достичь которые можно лишь с большим по норме управлением – собственные векторы этой матрицы, отвечающие ее малым собственным значениям. ПЕРВАЯ ИДЕЯ: взять в качестве X nxm-матрицу собственных векторов матрицы P, отвечающих ее m максимальным собственным значениям.
Если Q почти вырождена, то есть состояния, которые почти нельзя наблюдать – собственные векторы этой матрицы, отвечающие ее малым собственным значениям. ВТОРАЯ ИДЕЯ: взять в качестве X nxm-матрицу собственных векторов матрицы Q, отвечающих ее m максимальным собственным значениям.
ИДЕЯ СБАЛАНСИРОВАННОГО УСЕЧЕНИЯ: предварительно сделать замену переменных, после которой P=Q.

506
СБАЛАНСИРОВАННОЕ УСЕЧЕНИЕ
|
|
|
|
x |
|
Txold |
|
|
|
Замена переменных |
|
|
|
приводит |
|||||
|
dx |
Ax Cu |
y |
Ox |
|
|
|||
|
|
|
|
||||||
|
dt |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
к системе того же вида, но с матрицами |
|
|
|||||||
A |
TA T 1 |
|
O |
O T 1 |
C |
TC |
|||
|
|
old |
|
|
|
old |
|
old |
|
При этом |
P |
TP T |
|
Q |
T *Q T 1 |
||||
|
|
|
old |
|
|
|
old |
|
|
Таким образом |
PQ |
|
TPold Qold T 1 |
|
- преобразование |
||||
|
|
|
|
|
|
|
|
|
подобия |
(PQ) |
(PoldQold ) |
{ 1 |
|
n} |
-инвариант системы |
||||
j j1/ 2 - ГАНКЕЛЕВЫ СИНГУЛЯРНЫЕ ЧИСЛА
