Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный физико-технический университет (МФТИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

матан Бесов - весь 2012

.pdf

Скачиваний:

Добавлен:

03.06.2015

Размер:

16.85 Mб

Скачать

☆

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 1314 / 2914 15 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

f (−∞, +∞) → R

h (−∞, +∞) → R

[a, b] h [a, b]h = 0 [a, b]

(a, b) −∞ a < b +∞ ε > 0

! b

|f (x) − h(x)| dx < ε.

! ! " # (a, b) = (−∞, +∞) $ # # "

% f # & " " '#

(a, b) !

# (−∞, +∞)

( ! "−∞+∞ |f (x)| dx #

! ) ci −∞ = c0 < c1 < . . . < ck−1 < ck = = +∞ f # * # &

" # " & # ci i = 1 k − 1 +

) " #						−+∞∞ \|f (x)\| dx " "
ε > 0 A B η " −∞ < A <
< c1 ck−1 < B < +∞ η > 0							!
!		A	k−2		!	ci+1−η	!	+∞
		A				ci+1−η		+∞
		\|f \| dx +				\|f \| dx +			\|f \| dx < ε.
	−∞		i=1			ci+η		B
			i=1			%k−1
* # #

			" x (−∞, A)						(ci − η, ci + η)
		0,	" x (−∞, A)				i=1		(ci − η, ci + η)
fε(x) =				B,		∞ ,	i=1
fε(x) =				B,		∞ ,
			(		+ )
			" ) x.
		f (x)	" ) x.

, " fε # [A, B] - [A, B]

! +∞

	\|f (x) − fε(x)\| dx < ε.	./0
−∞
$ # 1 [A, B]
hε !	B
	\|fε(x) − hε(x)\| dx < ε.	.20
	A
" # hε " & '#
(−∞, A) (B, +∞) , " ./0 .20 #

! +∞

|f (x) − hε(x)| dx

−∞

! +∞ ! +∞

|f (x) −fε(x)| dx+ |fε(x) −hε(x)| dx < ε+ ε = 2ε.

−∞	−∞
, # "
	f

(a, b) −∞ a < b +∞ ε > 0

(a, b) ϕ

! b
\|f (x) − ϕ(x)\| dx < ε.		.30
a
	"

(−∞, +∞)

!
!	+∞
lim	\|f (x + η) − f (x)\| dx = 0.	.40
η→0	−∞

( f !

# (−∞, +∞) 5 " " # ε > 0 , "

ϕ "

.30 (a, b) = (−∞, +∞) ( ϕ = 0

[A, B] ( # 6 ϕ

# [A − 1, B + 1]

(−∞, +∞) ηε (0, 1)

			ε	η R : \|η\| ηε.
	\|ϕ(x + η) − ϕ(x)\| <
		B − A + 2
\|η\| ηε
!	∞	!	∞
	\|f (x + η) − f (x)\| dx		\|f (x + η) − ϕ(x + η)\| dx+
	−!∞∞	! −∞∞

+|ϕ(x+η)−ϕ(x)| dx+ |f (x)−ϕ(x)| dx < ε+ε+ε = 3ε.

−∞ −∞

! "

# $# ! % & f %

% & h ' ! ! % & h "

( '

∞

a1 + a2 + a3 + . . .	ak,	)
	k=1

' ak R ( ! ak * ' k

' ak !


	n
% & ! ' k Sn =	ak ( ! n
	k=1

+ '

{S	}∞			S
n	1 ' (- -!
. + S = lim Sn (
/	n→∞
/		∞
		∞

a1 + a2 + . . . = S			ak = S.
		k=1		∞
				∞

0 $ + a1 + a2 + . . . ak
#				k=1
#		}∞
1 {S		}∞
	n	1 -! ! )
,! ) ( ! S "
			∞

( 2 / #			ak = +∞

k=1

Sn → +∞ n → ∞ ∞ ak = −∞ Sn → −∞

k=1

n → ∞

3 ' $ ! ) "

! lim ak = 0

k→∞

4 ! - "

'- ! ! % "

1 − 1 + 12 − 12 + 13 − 13 + 14 − 14 + . . .

1 − 1 + 1 − 1 + 1 − 1 + . . .

Sn → S, Sn−1 → S n → ∞.

an = Sn − Sn−1 → 0 n → ∞.

! " #

$ "$

" % !

∞ 1

k=1 k $ $&

	2n
S2n − Sn =	1			1	n =	1		→ 0 n → ∞,
		k					2
			2n
	k=n+1

" " " & #

{Sn} {S2n}	$
% " (



	n+p
ε > 0 nε N :			< ε n N, n nε, p N.
ε > 0 nε N :		ak	< ε n N, n nε, p N.

	k=n+1

n+p

ak = Sn+p − Sn,

k=n+1

) * +

! #

* +

" #

! * +

, &
∞

an+1 + an+2 + . . .	ak
k=n+1

$ n

" * +

		∞		∞

!			ak	bk "
		k=1		k=1
		∞

λ, μ R (λak + μbk)
		k=1
	∞	∞	∞
	∞	∞	∞

	(λak + μbk) = λ	ak + μ	bk.
	k=1	k=1	k=1

" # "$

n	n	n

(λak + μbk) = λ	ak + μ	bk
k=1	k=1	k=1

- n → ∞

∞

ak, ak 0 k N.
k=1

k0 N 0 ak bk k k0

◦ ∞ bk

k=1

∞

k=1		∞
"◦		∞
"◦
		ak
	∞	k=1
	∞

	bk

k=1

◦ # ∞ bk $

k=1

&
	∞
		ak #
		ak #
	k=1
	∞

	ak

k=1

§
"◦ ' (				∞
"◦ ' (
					bk
			k=1					∞
								∞
									ak
) (									ak
								k=1
ak						> 0 bk	> 0 k N
							∞	∞
lim	ak	= L (0, ∞)
	ak						ak	bk
							ak	bk
k→∞ bk							k=1	k=1
							k=1	k=1


		k0 N :		1	Lbk ak 2Lbk k k0.
		k0 N :	2		Lbk ak 2Lbk k k0.
			2
$ * + λ = 0 "
		∞			∞

			ak			bk
		k=k0			k=k0

(

ak 0 bk 0 k
N ak = O(bk) k → ∞						∞
N ak = O(bk) k → ∞						bk
			∞			k=1
			∞

			ak
			k=1

	! " f			# [1, +∞)
				" +∞
	∞
	f (k)			1 f (x) dx
	k=1

-
		! k+1
		f (k)	f (x) dx f (k + 1)
		k
		! n+1
n		! n+1		n	n+1
f (k)		f (x) dx		f (k + 1) =	f (k).	"
k=1		1		k=1	k=2
k=1				k=1	k=2


							∞
								f (k)
								f (k)
							k=1	∞
								∞
									f (k)
									f (k)
"								k=1
"
	n+1	f (x) dx
	1	f (x) dx
f
" b					!"!#
1 f (x) dx b						" ∞
						1 f (x) dx!
	$ # % % !
& # ' % %
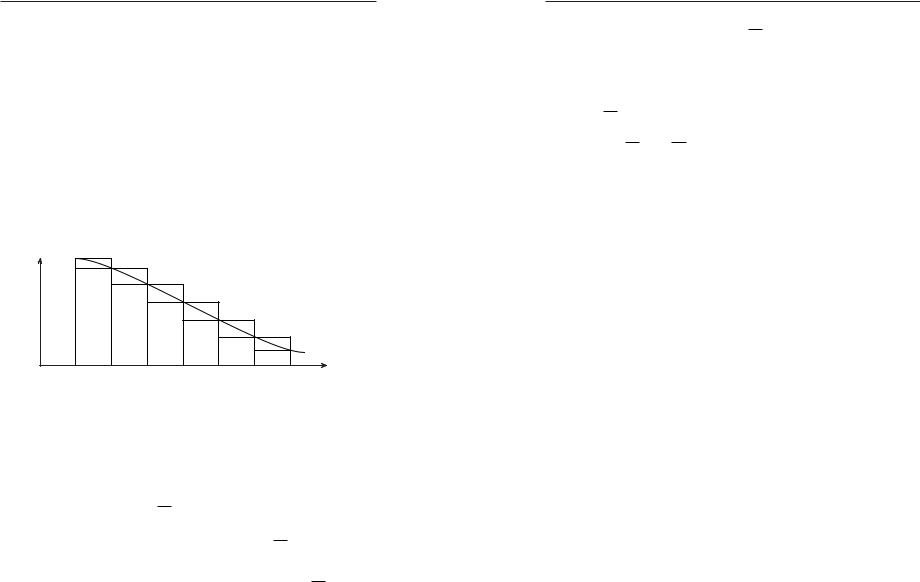
[1, n + 1] %
f !
	y
								y = f (x)
	0	1	2	3		k	k + 1	x
				( ! )!#

* % # ' %

' %

% # + ' %

, ' % % % !

	∞
(		k1α	α			0 ! !
	k=1
			∞	1
				1
-' % ! (					α
			k=1 k
α > 1 0 < α 1
					"	∞ 1
. .						1	xα	dx
α > 1 0 < α 1!

∞
	1		α 0
(	ln 1 +	kα	α 0
k=1
! ! -' % !				/
α > 1 0 < α				1! 0

α > 0

∞

k1α

α >

k=1

. # ! !

k → ∞!

> 0 ln 1 +

k1α

1 2

∞

-' % a

-3 a

a k=1

k+1! 4 .

k → ∞.

ak = o

6 . ! 0 . % .

. 3

S2n − Sn =

na2n.

k=n+1

7 5 8

(	∞
	∞
		qk
		qk
	k=0
0 < q < 1 q 1!					k k0!
0 0 < q < 1 qk				1
0 0 < q < 1 qk				2
		∞		k	∞
		∞	1		∞
9			1		qk
					qk
		k=1	k2 #
!		k=1			k=1
!

: , q 1 ! ! -' %

; ,

< .

1 − qn+1

qn+1

−

, q = 1.

Sn = q

1 − q

k=0

> 0

k N

◦

q < 1

ak+1

q < 1 k k0,

∞

◦

k=1

ak+1

1 k k0,

∞

k=1

1◦ k k0 ak+1 qak

ak qk−k0 ak0 = c0qk bk.

∞

k=1

∞

2◦ # ak+1 ak > 0 $%

∞

k=1

& '

k=1

ak > 0 k

lim

ak+1

= q.

k→∞

∞

◦

q < 1

k=1

∞

◦

q > 1

k=1

∞

(◦

q = 1

k=1

1◦ ε > 0 q q + ε < 1

k+1

q a k k

∞

k0 N

1 k k0

k=1

2◦

q > 1

∞

k=1

∞

◦ 1

α > 0

k=1

kα

ak+1

kα

1 α

→ 1 (k → ∞).

(k + 1)

1 +

∞

) 0 < α 1

k1α

α > 1

k=1

∞

ak+1

ak ak

−k

k=1

1 +

→ e−1 < 1 k → ∞ ' +

k + 1

ak 0 k N

◦

q < 1

k0 N

√

q < 1 k k0

∞

◦

k=1

√

k0 N k k0 :

∞

k=1

1◦

∞

qk k k

∞

k=1

◦

∞

! "

k=1

$ % & '

ak 0 k N

√

lim

k ak = q.

k→∞

∞

(◦

q < 1

k=1

∞

◦

q > 1

k=1

∞

)◦

q = 1

k=1

! *

√

! ! lim

= q " !

k ak

k→∞

lim

√

= q.

k→∞

+ * 1◦ $ q < q0 <

∞

< 1

, k0

√

< 1 k k0

N-

k=1

◦ / "

√

! k0

N k k0-

1 $ "

∞

k=1

∞

◦ 1

k=1 k

√

k=1

lim k

= 1

k→∞

∞								2
								k
		ak ak =		1		−	1

							k
k=2					k
√
& ' k	ak		= 1 −	1		→ e−1 < 1 k →
				k

→ ∞

$ ! & ' "

+ !

0 #

1 0 # & '

2 ! ( $ & '

+ "

! {qk}∞k=0

3 ! 0 4

∞ 1

+ k=1 kα α > 0 & "

1 + # !

! # #

& + "

# ! + "

∞

ak +

				k=1
				∞			\|a \|
							\|a \|
							k
				k=1
#
								∞
								\|ak\|
								k=1
+ & ' $

	n			n
		a				\|	m n,
		a		\|a		\|	m n,
	k=m		k	k=m	k

∞

k=1

∞

|a |

k=1

1 − 1 +

−

+ . . .

! "

#$% $

% &$ '

( (

	∞

)	ak & *
	k=1

k → nk $%
		∞

N ↔ N + (			ank $
		k=1			∞
					∞
						ak"
! $						ak"
			∞		k=1
			∞

				ak
		∞	k=1				∞
		∞					∞
		a					a
		k					k
		k=1					k=1

		∞		∞
					ak.
			ak	=	ak.		! "
		k=1		k=1
∞	,			-&$
∞				∞
a				\|a \| (
k=1		k		k=1	k
k=1				k=1
( .
		n	∞
		\|a \|	\|a \| n N.
		k		k
		k=1	k=1

/ ! "

	∞				n				n
) S		S
) S	a	S	n		a S		n		a
	k		n		k		n		k
	k=1				k=1			k=1
, * ( n N ' 0 N =
= N (n) > n ( Sn *
SN + ( m N
\|Sm − Sn\| \|an+1\| + \|an+2\| + . . . ρn,
( ρ									∞
( ρ				n(					\|a \|
n 1									k
									k=1
) 2 m → ∞
	\|S − S \|				ρ	n N.
	\|S − S \|				ρ	n N.
				n	n

3 ρn → 0 n → 0 % ( #

S	→ S n → ∞
n
! "
		∞	∞

		ak	bk
		k=1	k=1

	∞
	∞

	akj bmj ,		!4"
	j=1

! ! " # ! $

	∞	∞
∞	∞	∞

akj bmj =	ak	bk	.	!5"
j=1	k=1	k=1

, 6 !4" &$

(

&$ ( .
n		\|\|b			∞	∞
\|a	kj	\|\|b	mj	\|	\|a \|	\|b	\| .
	kj		mj		k	k
j=1					k=1	k=1

n2	n	n
			n N.
Sn2 akj bmj =	ak	bk	n N.
j=1	k=1	k=1

! n → ∞ "

{S				2	}∞
	∞					∞
			n		n=1

		ak				bk #
	k=1					k=1

& '( ' $%

)

ak ak+1 > > 0 k N ak → 0 k → ∞

	∞
	∞

	(−1)k+1ak = a1 − a2 + a3 − a4 + . . .		'
k=1		∞
		∞
	rn =	(−1)k+1ak

k=n+1


\|rn\| an+1.	*

+ , "

- {S2n}∞1 "

' .

S2n = (a1 − a2) + (a3 − a4) + . . . + (a2n−1 − a2n) =

= a1 − (a2 − a3) − (a4 − a5) − . . . − (a2n−2 − a2n−1) − a2n.

/ {S2n}∞1 0 S2n a1 0 "

{S	2n	}∞
	2n	1 .
lim S2n S [0, a1].
n→∞
{S2n−1}∞				"
		1		"
- {S			}∞
		n	1

S S2n−1 = S2n −

− a2n → S − 0 = S n → ∞ 1 "

% {S2n}∞1 {S2n−1}∞1

S Sn → S

n → ∞ ' S

rn 2 ' n" .

(−1)n+1rn = an+1 − an+2 + an+3 − an+4 + . . .

3 % "

45 "

*	∞	(−1)	k+1

,				α > 0 "
	k=1	kα
6 % 5

∞

akbk	, %
k=1
		n
		n

	Sn =	akbk.
	k=1

		k
B0 R, Bk B0 +
B0 R, Bk B0 +		bj	(k = 1, . . . , n).
		j=1
# bk = Bk − Bk−1 k = 1		n
	n	n	n

Sn =	ak(Bk − Bk−1) =		akBk − akBk−1.
	k=1	k=1	k=1

k k + 1

n	n−1

akbk = anBn − a1B0 −	(ak+1 − ak)Bk,
k=1	k=1

	n
akbk
	k=1

! B0 = 0

{ak}1∞
		∞

		bk
	∞	k=1
	∞

	akbk

k=1

" ! # $% & B0 =

= 0 $ '$

∞

akbk (

k=1

n → ∞

anBn → 0 n → ∞

! {Bn} an → 0 n → ∞

)

! %

# M sup |Bk|

		k N
∞	∞
\|(ak+1 − ak)Bk\| M	\|ak+1 − ak\| =
k=1	k=1		∞
			∞

			(ak+1
		= M	(ak+1

k=1

− ak) = M |a1|.

n → ∞

∞

akbk

k=1


∞				n
			\|a1\| sup		bk
		akbk	\|a1\| sup		bk	.
			n N
k=1				k=1

							∞
{a	}∞
{a	}∞						b	k
k	1						k=1	k
		∞					k=1
		∞

		akbk
		k=1		ak → a0 k → ∞
				ak → a0 k → ∞
αk ak − a0 → 0 k → ∞
∞			∞	∞

	akbk = αkbk + a0					bk.
k=1			k=1	k=1

!" "

" # $ %

& " "

' ( )* + %

, !" !

& ! " " %

∞
sin kx		, α > 0,		x R.	-
	kα	, α > 0,		x R.	-
	kα
k=1
ak =			1
ak =			kα

					n
$					sin kx
					k=1

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 1314 / 2914 15 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
28.08.201977.21 Кб7Лето 10 класс.docx
#
03.06.201562.17 Кб12Линал экзамен.pdf
#
09.11.20191.25 Mб37Логарифм. нерав.9.doc
#
17.07.20192.02 Mб6ман.docx
#
03.06.2015241.78 Кб40Массивы.pdf
#
03.06.201516.85 Mб31матан Бесов - весь 2012.pdf
#
03.06.201584.55 Кб14МатСтатистика. Программа.pdf
#
27.03.20165.39 Mб56Мессиа том 1.pdf
#
08.11.2018434.18 Кб17Метод.реком.по самост.работе -МПОСР-2011.doc
#
27.03.2016656.27 Кб115Методические указания. РТ цепи и сигналы. Озерский.pdf
#
27.11.2019594.94 Кб13Методичка по Деталям машин и ОК исправленная.doc