2.9.Эквивалентность игр в Байесовской форме

Мы говорим, что две игры Байеса

,

полностью эквивалентны тогда и только тогда, когда для каждого iєNсуществуют функции

и, такие, что

.

Используя критерий эквивалентности, мы можем для каждой игры Байеса поставить в соответствие игру Байеса с согласованными мнениями, если

и,.

- количество элементов во множестве.

2.10.Тип-агентное представление

В тип-агентном представлении существует один игрок-агент для каждого возможного типа каждого игрока в игре Байеса. Считаем, что

.

- количество агентов в тип-агентном представлении.

Агент t_iотвечает за выбор действий, которые бы игрок i использовал в Г^b, если бы t_iбыло бы действительным типом.

D_ti=С_i– множество стратегий агентаt_i.

Функция полезности для данного агента t_iєT_iопределяется как ожидаемый выигрыш игрокаiв Г^bпри условии, что типы остальных участников распределяются в соответствии с мнением игрока i, имеющего типt_i

Функции полезности

,

.

Обозначения:, еслиипоявляются в одной и той же формуле, тогда- это j-я компонента.

- тип-агентное представление игры Байеса

3.Равновесие в играх в стратегической форме

3.1. Равновесие по Нэшу

Рассмотрим игру в стратегической форме .

Смешанной стратегией игрока iназывается распределение вероятностей на множестве,,.

- множество всех смешанных стратегий игрокаi,, где.

Если игроки выбирают свои стратегии независимо, согласно набору стратегий , тогда вероятность того, что они выберут набор чистых стратегий , равняется.

– ожидаемая платаi-го игрока, если все игроки независимо выбрали чистые стратегии согласно.

.

– набор стратегий, в котором смешанная стратегияi-го игрока равна, а все остальные компоненты такие, как в.

обозначает случайную стратегию из, которая равна 1 на чистой стратегиии 0 для всех других чистых стратегий из.

, где.

Каждый игрок iвыбирает свои чистые стратегии так, чтобы максимизировать свой ожидаемый выигрыш, он с нулевой вероятностью выбирает стратегии, в которых максимум не достигается, т.е. если, тогда

(3.1.1)

Набор смешанных стратегий называется равновесным по Нэшу, если выполняется (3.1.1).

Набор смешанных стратегий является равновесным по Нэшу, если ни один из игроков не может увеличить свой ожидаемый выигрыш при одностороннем отклонении от договорного набора смешанных стратегий, т.е.

(3.1.2)

Тот факт, что (3.1.2) эквивалентно (3.1.1) – это следствие следующей леммы.

Лемма.

.

Более того, тогда и только тогда, когдатакого, что

.

Доказательство леммы:

.

есть среднее с весовыми коэффициентами членов, где. Такое среднее не может быть больше, чем максимум усредняемых членов. Оно строго меньше, если любой не максимальный член имеет положительный вес.

Набор чистых стратегий является равновесным в чистых стратегиях, если

.

Лемма 1 означает, что c– равновесие по Нэшу, если набор чистых стратегий, является равновесием в чистых стратегиях.

Теорема 3.1

Для конечной игры Г в стратегической форме существует по крайней мере, одно равновесие в смешанной стратегии из .

Пример

Игра, в которой существует равновесие по Нэшу в чистых стратегиях:

	3.0	0,2	0,3
	2,0	1,1	2,0
	0,3	0,2	3,0

1) Равновесие по Нэшу может быть не эффективным.

2) Может быть несколько равновесий в одной игре.

Исход игры оптимален по Парето, если не существует другого исхода, более выгодного для всех игроков. Например,

выбор является оптимальным по Парето в игре двух лицcфункциями выигрыша, если не существует другого выборадля которого имеют место неравенства

для всехи

хотя бы для одного i.

Пример(«Дилемма заключённого»)

	5,5	0,6
	6,0	1,1

- признаваться

- не признаваться

Выигрыш – сколько лет свободы будет у игрока в ближайшие шесть лет.

Точка (1,1), единственное равновесие по Нэшу, не эффективна по Парето, выигрыш (5,5) лучше. Интерпретация этой игры приведена в введении.

Пример («Семейный спор»)

Муж и жена решают, куда им пойти. Жена предпочитает идти за покупками в магазин, муж – на футбольный матч. Они счастливы, когда вместе и чувствуют себя неуютно, когда они врозь.

	3,1	0,0
	0,0	1,3

- идти на футбол,

- идти в магазин

Три равновесия (3,1), (1,3) и равновесие в смешанных стратегиях (0.75[]+0.25[], 0.25[]+0.75[]), которые дают каждому игроку ожидаемый выигрыш 0.75.

Как подсчитать ожидаемый выигрыш? Будем использовать функцию выигрыша

.

;;;

Для доказательства теоремы 3.1 понадобятся следующие сведения.

Точечно-множественным отображением называется любое отображение, которое ставит в соответствие каждой точкемножествотак, что.

Пусть - метрические пространства.

Отображение являетсяполунепрерывным сверху,если,и еслисходится к,сходится к, тогда.

Таким образом, полунепрерывно сверху, если множество- замкнутое множество. В частности, если- непрерывная функция,, тогда- полунепрерывное сверху точечно-множественное отображение. Т.е. полунепрерывное сверху отображение можно рассматривать как обобщение непрерывных функций.

Неподвижной точкой отображения является , т.ч..

Теорема Какутани о неподвижной точке.

Пусть S– непустое, выпуклое, ограниченное, замкнутое подмножество конечномерного векторного пространства. Пустьполунепрерывное сверху точечно-множественное отображение такое, что-- непустое выпуклое множествоS. Тогда существует, т.ч..

Для понимания роли различных предположений теоремы Какутани рассмотрим пример.

Пример

:

Н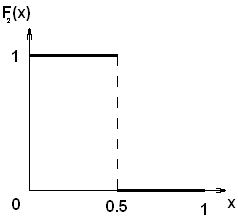ет неподвижной точки, нарушено предположение о полунепрерывности сверху, т.к.незамкнутое множество в точкеx=0.5,y=0.

Чтобы удовлетворить требованию полунепрерывности сверху, расширим отображение

=

Нет неподвижной точки, т.к. невыпуклое множество (выпуклостьS: если,,,).

Чтобы удовлетворить требованию выпуклости, расширим отображение

=

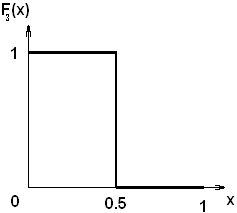
Есть неподвижная точка 0.5.удовлетворяет всем требованиям теоремы Какутани.

Доказательство теоремы 3.1.

- конечная игра в стратегической форме.

Множество - непустое, выпуклое, замкнутое, ограниченное множество.

(Sограничено, если существуетK>0 такое, что для любого)

K=N. Множествоявляется подмножеством, где.

Обозначим и любого игрока

.

Т.е. - множество лучших ответовj-ого игрока на комбинацию независимых смешанных стратегий других игроков.

По лемме - это множество всех распределений вероятностинатаких, чтотакого, что. Таким образом,выпукло.

непустое, т.к. включает.

Пусть - точечно-множественное отображение такое, что

, т.е., если.

- не пусто и выпукло, т.к. является произведением непустых выпуклых множеств.

R– полунепрерывно сверху.

Чтобы это показать, обозначим исходящиеся последовательности.

,,

,,

,

Для доказательства полунепрерывности сверху покажем, что ,,,.

По непрерывности ожидаемой функции полезности

Поэтому и

Таким образом - полунепрерывное сверху отображение. По теореме Какутани о неподвижной точке существует набор смешанных стратегийтакой, что, т.е., так что- это равновесие по Нэшу в.