
- •РАБОЧАЯ ТЕТРАДЬ
- •Задача 1.1
- •Справочный материал
- •Решение задачи 1.1
- •Задача 1.2
- •Решение задачи 1.2
- •Задача 2
- •Справочный материал
- •Решение задачи 2
- •Определение
- •Теорема (Связь абсолютной сходимости и сходимости)
- •Разложения основных элементарных функций в ряд Маклорена
- •Решение задачи 8
- •Задача 9.1
- •Решение задачи 9.1
- •Задача 9.2
- •Задача 10
- •Решение задачи 10
- •Задача 11

Задача 4
Исследовать ряд на абсолютную и условную сходимость:
∑ (−1) .
∞ n
n=1 n 3 ln (n +2)
Справочный материал
Признак Лейбница
∞
Если для членов знакочередующегося ряда ∑(−1)n+1 un ,
n=1
где un ≥ 0 , выполнены два условия:
• lim un = 0 ,
n→∞
• un+1 < un начиная с некоторого номера n > N0 ,
то ряд сходится и его сумма удовлетворяет неравенству
0 < S < u1 .
Определение
Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из модулей его членов. Если же знакопеременный ряд сходится, а ряд, составленный из модулей его членов расходится, то исходный ряд называется условно (неабсолютно) сходящимся.
Теорема (Связь абсолютной сходимости и сходимости)
Знакопеременный ряд u1 +u2 +u3 +K+un +K сходится,
если сходится ряд u1 + u2 + u3 +K+ un +K , составленный из
модулей его членов, т.е. из абсолютной сходимости вытекает сходимость исходного ряда.
Решение задачи 4
Так как из абсолютной сходимости вытекает сходимость знакочередующегося ряда, то исследуем вначале ряд, составленный из модулей членов заданного ряда
10

∞ |
|
|
1 |
|
∞ |
|
|
|
|
|
|
|
|
|
|
∑ |
|
|
= ∑un . |
|
|
Так |
как |
n -ый |
|
член ряда |
|||||
|
n 3 ln (n +2) |
|
|
||||||||||||
n=1 |
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
1 |
|
|
|
∞ |
1 |
|
|
||
un |
= |
|
~ |
|
= vn , |
а ряд |
∑ |
|
расходится |
||||||
|
|
1 |
|
1 |
|
||||||||||
|
|
|
n 3 ln (n +2) n→∞ n ln |
3 |
n |
|
n=1 |
n ln |
3 |
n |
|||||
(см. справочный материал к задаче 3), следовательно, ряд из модулей членов исходного ряда расходится по 2-ому (предельному) признаку сравнения и абсолютной сходимости нет.
Исходный ряд знакочередующийся, поэтому используем признак Лейбница:
|
lim u |
n |
= lim |
|
1 |
|
= 0 (выполнено), |
|
|
|
|
|
|
||||||
|
n→∞ |
n→∞ n 3 ln (n +2) |
|
|
|
||||
|
un = |
|
1 |
|
, |
un+1 = |
1 |
, значит |
|
n 3 ln (n +2) |
(n +1)3 ln (n +3) |
||||||||
un+1 < un , п =1, 2, 3,K.
Таким образом, исследуемый ряд сходится по признаку Лейбница и сходимость условная.
∞
Ответ: ∑ - сходится условно. n=1 n 3 ln (n +2)
Задача 5
Вычислить приближенно сумму ряда с заданной точностью ε . Указать N - наименьшее число членов ряда, которое обеспечивает заданную точность суммы ряда:
∑∞ (−1)n , ε =10−3 .
n=1 3n n
11
Справочный материал
|
|
|
|
|
У |
сходящегося |
|
|
|
|
знакочередующегося |
|
ряда |
||||||||||||
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
∑(−1)n+1 un = S |
модуль |
остатка ряда после |
n -ого |
члена |
|||||||||||||||||||||
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
rn |
|
= |
|
un+1 −un+2 +un+3 −K |
|
|
не превосходит модуля |
первого |
||||||||||||||||
|
|
|
|
||||||||||||||||||||||
отброшенного члена |
|
|
rn |
|
≤ un+1 . |
|
|
|
|||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
Отсюда погрешность от замены суммы ряда |
S |
его |
n -ой |
|||||||||||||||||
частичной суммой Sn : |
|
S −Sn |
|
= |
|
rn |
|
≤ un+1 . |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
Решение задачи 5
Исследуемый ряд является знакочередующимся. Модуль общего члена un = 3n1 n . Очевидно, что с ростом n :
1) модули членов ряда убывают: 13 > 321 2 > 331 3 >K .
2) lim un = lim 3n1 n = 0 .
n→∞ n→∞
Таким образом, исследуемый ряд сходится по признаку Лейбница и к его остатку после n -ого члена
rn = (−1)n 3n+1 (1n +1)− 3n+2 (1n +2)+ 3n+3 (1n +3)−K
применима оценка: rn ≤ |
1 |
= un+1 , т.е. для вычисления |
3n+1 (n +1) |
суммы нашего ряда с заданной точностью ε = 0.001 достаточно выполнения неравенства:
un+1 = 3n+1 (1n +1) ≤ 0.001 .
12
Отсюда |
подбором |
легко |
получить, |
что |
n ≥ 4 . |
|||||
Действительно, |
u4 = |
1 |
= |
|
1 |
. |
Таким |
образом, |
для |
|
35 5 |
1215 |
|||||||||
|
|
|
|
|
|
|
||||
вычисления суммы исходного ряда с заданной точностью достаточно взять четвёртую частичную сумму:
|
S ≈ S4 = − |
1 |
+ |
1 |
− |
|
1 |
+ |
|
1 |
|
= − |
|
31 |
. |
|
|
|
|
|
|||||||||
|
3 |
|
|
|
|
324 |
108 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
18 |
|
|
81 |
|
|
|
|
|
|
|
|
|||||||||||||
|
∞ |
(−n |
1) |
n |
|
|
|
|
31 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответ: ∑ |
|
≈ − |
|
, n = 4 . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
n=1 |
3 |
|
108 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
Задача 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Найти область сходимости степенного ряда: |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
∑n!(x n+1) |
n |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
n=1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Справочный материал |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Теорема Абеля |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
Для |
каждого |
степенного |
ряда |
|
|
∑an (x −a)n |
существует |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
||
такое неотрицательное |
число |
|
r ≥ 0 , |
что ряд ∑an (x −a)n |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=0 |
|
|
|
||
сходится, |
и притом |
|
абсолютно, |
|
при |
|
|
|
x −a |
|
< r |
|
|||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||
x (a −r; a +r ) |
и |
|
расходится |
|
|
при |
|
|
x −a |
|
> r |
|
|||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||
x (−∞; a −r ) (a +r; +∞). |
Число |
|
|
r |
|
называется |
|
радиусом |
|||||||||||||||||||||
сходимости, а открытый промежуток |
|
(a −r; a +r ) интервалом |
|||||||||||||||||||||||||||
сходимости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13

ЗАМЕЧАНИЕ
Относительно поведения степенного ряда на границах промежутка сходимости, т.е. при x = a +r и x = a −r общих
∞ |
∞ |
утверждений высказать нельзя. Ряды ∑an rn |
и ∑an (−r )n |
n=0 |
n=0 |
могут сходиться или расходиться в зависимости от их конкретного вида.
Поэтому, принят следующий порядок отыскания области сходимости степенного ряда:
1)При помощи признака Даламбера или радикального признака Коши (см. компендиум по дисциплине «Математика», Тема 4 «ТЕОРИЯ ПРЕДЕЛОВ») отыскивают интервал сходимости
степенного ряда, решая относительно x неравенства:
lim |
|
|
un+1 (x) |
|
|
<1 или lim n un (x) <1 . |
|
|
|||||
|
|
un (x) |
|
|||
n→∞ |
|
|
|
n→∞ |
||
2)Исследуют сходимость ряда на концах промежутка сходимости, т.е. при x = a +r и x = a −r .
Решение задачи 6
|
|
|
Найдем |
|
|
интервал |
|
сходимости |
степенного |
ряда |
|||||||||||||||
∞ |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
∑ |
n!(x +1) |
|
|
|
|
, используя признак Даламбера |
|
|
|||||||||||||||||
|
|
n |
|
|
|
|
|
|
|||||||||||||||||
n=1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
un+1 |
|
|
|
|
|
|
|
|
(n +1)!(x +1)n+1 |
|
|
|
x +1 |
|
|
(n +1)= ∞, x ≠ −1. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
lim |
|
|
= lim |
|
|
3n+1 |
|
|
|
|
|
= |
|
|
lim |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
un |
|
n!(x + |
1) |
n |
|
3 |
|
|||||||||||||||||
n→∞ |
|
|
n→∞ |
|
|
|
|
|
|
|
|
n→∞ |
0, x = −1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как по признаку Даламбера ряд сходится при условии, |
||||||||||||||||||||||
|
|
|
un+1 |
|
|
= l <1 (в частности |
l = 0 ), значит, исходный ряд |
||||||||||||||||||
что |
lim |
|
|
|
|||||||||||||||||||||
|
|
||||||||||||||||||||||||
|
|
n→∞ |
|
un |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сходится абсолютно только в точке x = −1 .
Ответ: {−1}.
14
Задача 7
Найти область сходимости степенного ряда:
∑ (n x −2) |
. |
∞ |
n |
|
n=1 5 2n +1
Решение задачи 7
Найдем интервал сходимости заданного степенного ряда, используя признак Даламбера
|
|
|
|
|
|
|
(x −2)n+1 |
|
|
|
|
|
|
(x −2)n+1 5n |
2n +1 |
|
|
x −2 |
|
|
|
2n |
|
|
|
x −2 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
lim |
|
5n+1 |
2n +3 |
|
|
= lim |
= |
|
|
lim |
|
= |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
(x −2)n 5n+1 2n +3 |
|
|
|
|
|
2n |
|
5 |
|
|
|
||||||||||||||||||||||||||||||
|
n→∞ |
|
|
|
|
(x −2)n |
|
|
|
|
|
|
|
n→∞ |
5 |
|
|
n→∞ |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
5n |
2n +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
(x −2) |
n |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
По признаку Даламбера ряд ∑ |
|
|
|
|
|
|
сходится, |
если |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
5 |
2n +1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x −2 |
|
|
|
|
|
|
< 5 −5 < x −2 < 5 |
−3 < x < 7 . |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
<1 |
|
x −2 |
|
Значит, |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
5 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
заданный ряд в интервале −3 < x < 7 сходится абсолютно. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
5 |
n |
|||||
|
|
|
|
|
|
|
При x = 7 исходный ряд превратится в ряд ∑ |
|
|
|
|
, |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
5 |
n |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
2n +1 |
|||||||
который |
|
после |
|
|
упрощений |
можно |
|
|
записать |
|
в |
|
|
виде: |
|||||||||||||||||||||||||||||||||||
|
∞ |
1 |
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
∑ |
|
|
= |
∑un |
|
|
|
(1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
n=1 |
|
|
2n +1 |
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
Поскольку u |
n |
= |
|
1 |
|
|
|
~ |
1 |
|
|
|
= v , а ряд |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n +1 n→∞ |
2n2 |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
1 |
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ |
|
|
= ∑vn |
|
|
|
|
|
(2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
2 |
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
15
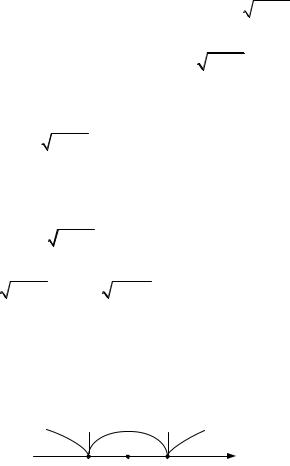
расходится |
как |
обобщённый |
гармонический с |
порядком |
||||||
p = 1 <1, |
то по |
2-ому признаку |
сравнения |
исследуемый ряд |
||||||
2 |
|
|
|
|
|
|
|
|
|
|
расходится при x = 7 . |
|
|
|
|
|
|
|
|
||
|
|
|
|
∞ |
|
|
(−5) |
n |
||
|
|
|
|
|
|
|
|
|||
При x = −3 исходный ряд имеет вид ∑ |
|
|
|
. После |
||||||
5 |
n |
|
||||||||
|
|
|
|
n=1 |
|
2n +1 |
||||
|
|
|
∞ |
(−1) |
n |
|
|
|||
|
|
|
|
|
|
|
|
|||
упрощений его можно записать в виде: ∑ |
|
|
|
(3). Ряд |
||||||
2n + |
1 |
|
||||||||
|
|
|
n=1 |
|
|
|
||||
из модулей членов ряда (3) это ряд (1), а потому он расходится.
|
|
∞ |
(−1) |
n |
|
|
|
|
||||
Сам же ряд |
∑ |
|
|
|
|
|
знакочередующийся, поэтому можно |
|||||
|
|
2n +1 |
||||||||||
|
|
n=1 |
|
|
|
|
|
|||||
использовать признак Лейбница. |
|
|||||||||||
По признаку Лейбница, так как |
|
|||||||||||
1) lim un |
= lim |
|
1 |
|
|
|
= 0 , |
|
|
|||
|
2n +1 |
|
||||||||||
n→∞ |
n→∞ |
|
|
|
|
|
||||||
2) un = |
|
1 |
|
|
, un+1 = |
|
1 |
|
un < un+1 , п =1, 2, 3,K, |
|||
|
2n +1 |
|
2n +3 |
|||||||||
|
|
|
|
|
|
|
|
|||||
то ряд (3) сходится.
Следовательно, промежуток сходимости степенного ряда [−3; 7), причём при x (−3; 7) - ряд сходится абсолютно, а при x = −3 - условно.
3 |
2 |
7 |
x |
|
Рис.1
16
