
- •РАБОЧАЯ ТЕТРАДЬ
- •Составитель – Леора С.Н.
- •Данный типовой расчет содержит задачи по теме «Обыкновенные дифференциальные уравнения».
- •Справочный материал
- •Процесс нахождения решения обыкновенного дифференциального уравнения называется интегрированием и требует умения вычислять интегралы.
- •Задача 1
- •Справочный материал
- •Решение задачи 1
- •Вариант №6.

∫ |
M1 |
(x) |
dx + ∫ |
N2 |
(y) |
dy = C . |
N1 |
(x) |
M 2 |
|
|||
|
|
(y) |
||||
Получим общий интеграл уравнения ψ(x, y)= C .
Решение задачи 1
Данное уравнение является уравнением с разделяющимися переменными. Разделяя переменные, путем
деления уравнения на выражение (1+ x2 ) (1+ y2 ), получим
x y
( )dx + ( )dy = 0 .
1 + x2 1 + y2
Интегрируем полученное уравнение:
∫ ( x )dx + ∫ ( y )dy = C .
1 + x2 1 + y 2
Получаем его общий интеграл 12 ln(1 + x2 )+ 12 ln(1 + y 2 )= C , или
ln(1 + x2 )+ln(1 + y2 )= 2C .
Так как C - произвольная постоянная, представим правую часть в виде 2C = ln C1 , получим ln(1 + x2 )+ln(1 + y 2 )= ln C1 .
Отсюда по свойству логарифма (1 + x2 ) (1 + y 2 )= C1 , или
(1 + x2 ) (1 + y 2 )= C1 .
Так как C1 - произвольная постоянная, общее решение исходного уравнения можно записать в виде:
(1 + x2 ) (1 + y 2 )= C .
Ответ: (1 + x2 ) (1 + y 2 )= C .
Задача 2
Найти решение задачи Коши:
y′+ 2xy = 2x , y(0) = 2 .
Справочный материал
5

Определение 1. Задача, в которой требуется найти решение дифференциального уравнения F(x, y, y′)= 0 или y′ = f (x, y), удовлетворяющее начальному условию y(x0 )= y0 , называется
задачей Коши.
Задача Коши решается в два этапа. Сначала находится общее решение исходного уравнения, а затем ищется частное решение, удовлетворяющее начальному условию.
Исходное уравнение является линейным дифференциальным уравнением первого порядка относительно y . Общий вид такого
уравнения:
y′+ p(x)y = g(x).
Линейное дифференциальное уравнение первого порядка можно решать двумя методами – методом Лагранжа и методом Бернулли (см. компендиум по теме “Обыкновенные дифференциальные уравнения”, пункт 9.2.3)
Решение задачи 2
Решим уравнение двумя методами.
Метод Бернулли. Положим y = u v , где u = u(x) и v = v(x) -
неизвестные функции. Тогда исходное уравнение перепишется в
′ |
+uv |
′ |
|
′ |
′ |
+ 2vx) = 2x . |
виде u v |
|
+ 2xuv = 2x , или u v +u(v |
|
|||
Выберем |
функцию v = v(x) |
так, чтобы v′+ 2xv = 0 . Тогда |
||||
′ |
|
|
|
вместо |
исходного линейного |
|
u v = 2x . Следовательно, |
||||||
уравнения нужно решить систему двух уравнений с разделяющимися переменными.
v′+ 2xv |
= 0 |
′ |
. |
u v = 2x |
|
Запишем первое из уравнений в виде dvv + 2xdx = 0 . Это
уравнение с разделяющимися переменными. Общий интеграл этого уравнения имеет вид:
∫ dvv + ∫2xdx = С.
6
Выберем какое-либо частное решение этого уравнения.
Пусть, например, С = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Интегрируя уравнение, получим ln |
|
v |
|
= −x2 |
v = e−x2 . |
|||||||||
|
|
|
|
|||||||||||||
|
|
Теперь решаем |
второе |
уравнение. |
Подставив |
в него |
||||||||||
найденную функцию v = e |
−x |
2 |
|
|
|
|
|
′ −x2 |
= 2x . |
|
||||||
|
|
, получим u e |
|
|||||||||||||
|
|
Так как |
u′ = |
du |
, |
|
следовательно, |
|
можно |
написать |
||||||
|
du |
dx |
|
|
||||||||||||
|
= 2xex2 . |
Умножив |
обе |
|
части уравнения |
на dx , |
получим |
|||||||||
|
dx |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du = ∫2xe x2 dx u = ex2 +С .
Таким образом, общим решением данного уравнения является: y = uv = (ex2 +С)e−x2 =1 +Сe−x2 .
Подставляя исходные данные задачи Коши в общее решение, найдем значение произвольной постоянной C .
y(0) = 2, 2 =1 +С, С =1.
Окончательно, решение задачи Коши имеет вид y =1 + e−x2 . Ответ: y =1 + e−x2 .
Метод Лагранжа. Сначала решим соответствующее однородное линейное уравнение y′+ 2xy =0.
|
Имеем |
dy |
= −2xdx . Это – |
уравнение с разделяющимися |
|||||||
|
y |
||||||||||
|
|
|
|
|
|
|
|
|
|
||
переменными. |
Общий интеграл |
этого |
уравнения имеет вид |
||||||||
∫ |
dy |
+ ∫2xdx = C . Интегрируя, получим |
ln |
|
y |
|
+ x2 = C , отсюда |
||||
|
|
||||||||||
|
|||||||||||
|
y |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
y = Сe−x2 .
Решение исходного неоднородного уравнения будем искать в виде y = С(x)e−x2 , где С(x) - неизвестная функция. Имеем
7

y |
′ |
′ |
|
−x2 |
− |
2xС(x)e |
−x2 |
. |
Подставим |
|
y и |
y |
′ |
в |
исходное |
|||||
|
= С (x)e |
|
|
|
|
|
||||||||||||||
уравнение, тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
′ |
−x2 |
− 2xC(x)e |
−x2 |
+ |
2xC(x)e |
−x2 |
= 2x , отсюда |
|
|
|||||||||
|
|
C (x)e |
|
|
|
|
|
|
|
|||||||||||
|
|
′ |
−x2 |
= 2x , или |
|
С(x) = ∫2xe |
x2 |
dx , |
С(x) |
= e |
x2 |
+С1 |
||||||||
|
|
С (x)e |
|
|
|
|
|
|||||||||||||
Таким образом, |
y = (ex2 +С )e−x2 или |
y =1 +С e−x2 |
– |
общее |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
решение исходного уравнения. Решим задачу Коши. Подставим начальные данные y(0) = 2 2 =1 +С1 С1 =1
Ответ: y =1 + e−x2 .
Задача 3
Найти решение задачи Коши. cosdxy + (x − 2sin y)dy = 0 , y(0) = 0 .
Справочный материал
Если переменная x входит линейно в множитель при dy и
совсем не входит в множитель при dx , это уравнение можно привести к линейному уравнению относительно x , то есть к
уравнению |
x′+ p(y)x = g(y). Методы |
решения линейных |
|||||
уравнений рассмотрены в Задаче 1. |
|
||||||
|
|
|
|
Решение задачи 3 |
|
||
Приведем исходное уравнение к виду x′+ x cos y = sin 2 y . |
|||||||
Это линейное уравнение |
относительно |
x . Решим задачу |
|||||
методом Бернулли. Положим x = u v , тогда |
|
||||||
|
|
|
′ |
|
′ |
−uv cos y = sin 2 y , |
|
|
|
|
u v +uv |
|
|||
′ |
|
′ |
−v cos y) = sin 2 y . Решение уравнения сводится к |
||||
или u v +u(v |
|
||||||
решению системы:
8
v′−v cos y = 0 |
. |
′ |
|
u v = sin 2 y |
|
|
Сначала решаем уравнение v′− v cos y = 0 . Запишем его в |
||||||||||||
виде |
dv |
= cos ydy , проинтегрируем |
ln |
|
v |
|
= sin y , или v = esin y . |
||||||
|
|
||||||||||||
|
|||||||||||||
|
|
|
v |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
Теперь решаем второе уравнение |
|
|
|
|||||||||
′ |
sin y |
|
|
du |
−sin y |
|
|
|
|||||
u e |
|
|
= sin 2 y , или |
|
= sin 2 y e |
|
|
|
. Умножив уравнение на |
||||
|
|
dy |
|
|
|
||||||||
dy , получим |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
du = sin 2 y e−sin y dy . |
||||||||
Это уравнение с разделяющимися переменными. Общий интеграл имеет вид
∫du = ∫sin 2 y e−sin y dy +С.
Возьмем интеграл ∫sin 2 y e−sin y dy .
∫sin 2 y e−sin y dy = ∫2sin y cos y e−sin y dy . Так как cos ydy = −d(−sin y) ,
∫2sin y cos y e−sin y dy = −∫2sin y e−sin y d(−sin y).
Полученный интеграл берется по частям.
Отсюда найдем u = 2e−sin y (−sin y −1) +С, тогда решение
исходного уравнения имеет вид:
x = uv = (2e−sin y (−sin y −1) +С)esin y = −2(sin y +1) +Сesin y .
Подставим начальные значения задачи Коши и найдем значение произвольной постоянной С.
y(0) = 0 0 = −2(sin 0 +1) +Сesin o 0 = −2 +С С = 2 Ответ: x = −2(sin y +1) + 2esin y .
9

Задача 4
Найти общий интеграл дифференциального уравнения.
(2xy −5)dx +(3y2 + x2 )dy = 0
Справочный материал
Уравнение вида
M (x, y)dx + N(x, y)dy = 0
будет уравнением в полных дифференциалах, если выполнено
∂M = ∂N
условие ∂y ∂x . Тогда общий интеграл уравнения можно
найти двумя способами.
1 способ. Общий интеграл уравнения в полных производных находится по формулам
x |
y |
∫M(x, y0 )dx+ ∫N(x, y)dy =C |
|
x0 |
y0 |
или |
|
x |
y |
∫M(x, y)dx+ ∫N(x0 , y)dy =C , |
|
x0 |
y0 |
где x0 и y0 - любые значения, входящие в область определения
функций M (x, y) и N(x, y). Их выбирают таким образом, чтобы полученный интеграл легче вычислялся, чаще всего принимают
x0 = 0 и y0 = 0 .
2 способ. Общий интеграл уравнения находится из условия
∂∂My = ∂∂Nx .
Решение задачи 4
Проверим, что данное уравнение является уравнением в
полных дифференциалах, то есть |
∂M |
= |
∂N . |
|
∂y |
|
∂x |
10
Здесь M (x; y) = 2xy −5 , а N (x; y) = 3y2 + x2 .
∂M |
= 2x ; |
∂N |
= 2x |
∂M |
= |
∂N |
. |
∂y |
∂x |
∂y |
|
||||
|
|
|
∂x |
||||
Следовательно, условие выполнено, и уравнение является уравнением в полных дифференциалах.
1 способ.
Запишем уравнение в виде его общего интеграла
x |
y |
∫(2xy −5)dx + ∫(3y2 + x2 )dy = C; |
|
x0 |
y0 |
Выбираем вариант подстановки: либо в первом |
|
подынтегральном выражении полагаем x = x0 , либо во втором |
|
полагаем y = y0 .
Выберем подстановку со вторым подынтегральным выражением.
x |
y |
|
|
||
∫(2xy −5)dx + ∫(3y2 + x02 )dy = C; |
|||||
x0 |
y0 |
|
|
||
Пусть x0 = 0 |
и y0 = 0 , тогда |
|
|
||
x |
|
|
y |
|
|
∫(2xy −5)dx + ∫3y 2 dy = C . |
|||||
0 |
0 |
|
|
||
Вычислим интегралы: |
|
|
|||
|
(x2 y −5x) |
|
x + y3 |
|
y = C; |
|
|
|
|||
|
|
|
0 |
|
0 |
|
|
|
|||
Подставив пределы интегрирования, получим:
x2 y −5x + y3 = C .
11

Общий интеграл уравнения имеет вид x2 y −5x + y3 = C .
2 способ.
Так как уравнение в полных дифференциалах, следовательно существует функция u(x, y), такая что
(2xy −5)dx +(3y2 + x2 )dy = du(x, y).
Тогда для функции u(x, y) справедливы следующие равенства:
∂u |
= 2xy −5 , а |
∂u |
= 3y2 + x2 . |
∂x |
|
∂y |
|
Проинтегрируем равенство ∂∂ux = 2xy −5 по x , получим
u = yx2 −5x +ϕ(y). Найдем ∂∂uy = x2 +ϕ′(y). С другой стороны
∂u |
|
2 |
|
2 |
|
|
2 |
′ |
2 |
|
2 |
|
∂y |
= 3y |
|
+ x |
|
. Следовательно, |
x |
|
+ϕ (y)= 3y |
|
+ x |
|
, или |
ϕ′(y)= 3y2 .
Найдем ϕ(y)= ∫3y2 dy = y3 . Следовательно, u = yx2 −5x + y3 .
Общий интеграл уравнения имеет вид u = C , то есть
yx2 −5x + y3 = C .
Ответ: x2 y −5x + y3 =C .
Задача 5
Методом изоклин построить интегральную кривую, проходящую через точку М.
y′ = − xy , M (0;1).
Справочный материал
Дифференциальное уравнение вида y′ = f (x, y)
12

в каждой точке плоскости (x, y) задает направление касательных
к интегральным кривым или поле направлений. Линии, на которых поле направлений постоянно, называются изоклинами. Из определения изоклин следует, что их уравнение имеет вид
f (x, y)= C ,
где C - любое постоянное число.
Решение задачи 5
Найдем уравнение изоклин. По определению уравнение имеет вид f (x, y)= C . Следовательно, уравнение изоклин в
данном случае имеет вид
− xy = C ,
или y = −Cx .
При C =1 уравнение изоклины имеет вид y = −x . На этой
изоклине |
поле направлений имеет угол наклонаα, такой что |
tg α =1, |
следовательно, α = 45° . Аналогично находим, что при |
C = −1 уравнение изоклины y = x . На этой изоклине tg α = −1,
α =135° . |
При C = 0 |
уравнение изоклины |
x = 0 , на изоклине |
tg α = 0 , |
α = 0° . При |
C = ∞ уравнение |
изоклины y = 0 , на |
изоклине tg α = ∞, α = 90° .
Изоклины и поле направлений приведены на рисунке 1. Поле направлений дает возможность установить, что интегральными кривыми являются концентрические окружности с центром в начале координат.
13
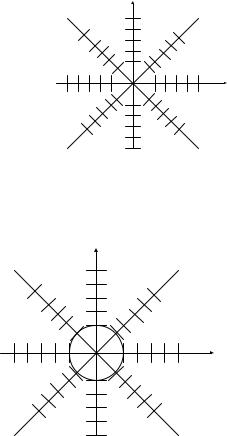
y |
x |
Рис.1 |
На рисунке 2 изображена интегральная кривая, проходящая через точку M (0;1).
y |
x |
Рис. 2. |
Задача 6 |
Найти кривую, проходящую через точку M (1;1) у которой
отрезок любой касательной, заключенный между точкой касания и осью абсцисс, делится осью ординат пополам.
Справочный материал
Данная геометрическая задача сводится к решению обыкновенного дифференциального уравнения. Исходя из
14
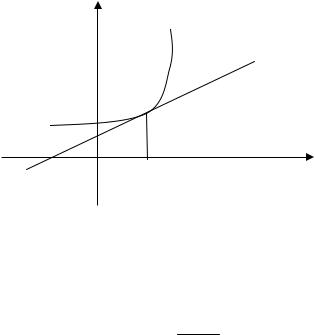
условий задачи, вначале необходимо составить дифференциальное уравнение, а затем его решить.
Решение задачи 6
Уравнение касательной, проходящей через точку (xm , ym ), имеет вид y − ym = y′(xm )(x − xm ).
М
N
х0 хm
Точка N лежащая на оси абсцисс имеет координаты (x0 ;0),
кроме того она лежит на касательной, следовательно
− ym = y′(xm )(x0 − xm ).
Найдем отсюда x0 :
y
x = − (m )+ x .
0 y′ xm m
Кроме того x0 = −xm . Отсюда
|
|
ym |
|
|||
− xm = − |
|
+ xm , |
||||
y′(xm ) |
||||||
2xm = − |
ym |
|
. |
|||
y′(xm ) |
||||||
|
|
|
||||
15
В силу произвольности точки (xm , ym ) получим уравнения для нахождения искомой кривой:
|
|
|
|
|
|
|
2x = − |
y |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
y′ |
||||||||||||||
Это уравнение с разделяющимися переменными. |
|||||||||||||||||||||||
2 |
y′ |
= − |
1 |
, или 2 |
dy |
= − |
dx |
. Отсюда 2 ln |
|
y |
|
−ln |
|
x |
|
= ln |
|
C |
|
. |
|||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
y |
|
x |
|
y |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Уравнение искомой кривой имеет вид y2 = Cx .
Найдем кривую, проходящую через точку M (1;1). Подставив в
уравнение |
y2 = Cx значения х =1 и у =1, получим |
С =1 . |
Следовательно, искомая кривая задается уравнением y2 |
= x . |
|
Ответ: |
y2 = x . |
|
Задача 7
Найти общее решение дифференциального уравнения
y′′′ctgx = 2 y′′.
Справочный материал
Если уравнение вида F(x; y(k ) ; y(k +1) ;...; y(n) ) = 0 не содержит явно искомой функции, то его порядок можно понизить на k единиц, положив y(k ) = p(x) .
Тогда
y(k +1) = p′;…; y(n) = p(n−k ) ,
и уравнение примет вид F(x; p; p′;...; p(n−k ) ) = 0 .
Решение задачи 7
Дано дифференциальное уравнение третьего порядка. Оно относится к типу уравнений, допускающих понижение порядка и не содержащих явно искомой функции y . Полагаем y′′ = p , где
p = p(x) , тогда y′′′ = p′ и исходное уравнение примет вид:
16

p′ctgx = 2 p , или p′− ctgx2 p = 0 .
Это уравнение с разделяющимися переменными. Запишем его в виде
|
|
|
|
|
|
|
|
|
|
|
|
|
dp |
|
|
− |
2 p |
|
|
= 0 , или |
dp |
− |
2dx |
= 0 . |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
ctgx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
ctgx |
|
|
|
|
|
|
|
|
|||||||||||||||
Интегрируя |
это |
|
уравнение, |
|
|
|
|
получим |
ln |
|
p |
|
|
+ 2 ln |
|
cos x |
|
= С , |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
или ln |
|
|
p |
|
|
+ 2 ln |
|
cos x |
|
|
= ln С1 , ln |
|
|
p |
|
= −2 ln |
|
cos x |
|
+ ln С1 ; |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
p |
|
|
|
|
|
|
С1 |
|
; p = |
С1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
ln |
|
|
|
= ln |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
cos2 x |
|
cos2 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Возвращаясь к исходной переменной, получаем |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
y′′ = |
|
|
С1 |
|
|
|
; y′ |
|
= С1 ∫ |
|
|
dx |
|
|
|
|
|
= С1tgx +С2 . |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
2 |
x |
|
|
|
2 |
x |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Рассмотрим интеграл ∫tgxdx = ∫ |
|
sin x |
dx =− ∫ |
d cos x |
|
|
=ln |
|
cos x |
|
. |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos x |
|
|
|
|
cos x |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Отсюда общее решение исходного уравнения:
y = С1 ∫tgxdx +С2 ∫dx = −С1 ln cos x +С2 x +С3 .
Ответ: y = −С1 ln cos x +С2 x +С3 .
Задача 8
Найти |
решение задачи Коши |
y′′ =16sin y cos y , |
y(0)= π/ 2 |
′ |
|
, y (0)= 4 . |
|
Справочный материал
17

|
|
Если |
уравнение |
|
вида |
F( y; y(k ) ; y(k +1) ;...; y(n) ) = 0 не |
||||||||
содержит |
явно |
независимую |
переменную |
х, то его |
порядок |
|||||||||
можно понизить, положив y(k ) |
= p( y) . |
|
|
|
||||||||||
|
|
Для |
уравнения |
|
|
|
|
′ |
′′ |
делается |
замена |
|||
|
|
|
вида F( y; y ; y |
) = 0 |
||||||||||
y |
′ |
= p . |
|
|
′′ |
|
|
dp |
|
|
|
|
|
|
Тогда |
y |
= p dy . |
Подстановка полученных |
формул |
||||||||||
|
|
|||||||||||||
сводит исходное уравнение к уравнению с разделяющимися переменными.
Решение задачи 8
Исходное уравнение не содержит независимую переменную. Заменой y′ = p и y′′ = p dpdy
виду p p′ =16sin y cos y . Это уравнение с разделяющимися
переменными. Запишем его в виде |
p dp =16sin y cos ydy и |
||||||||||
проинтегрируем. Получим последовательно |
|
|
|
||||||||
|
|
|
∫ p d p = ∫16siny cos ydy , |
|
|
|
|||||
∫ |
p d p = |
∫ |
16siny d(sin y), |
|
p2 |
=16 |
sin 2 |
y |
+C , |
||
|
|
|
|
||||||||
|
|
|
2 |
|
|
2 |
1 |
||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
p2 =16sin 2 |
y +C . |
|
|
|
||||
|
|
|
|
|
|
|
1 |
|
|
|
|
Воспользуемся начальными данными y(1) |
|
|
′ |
||||||||
= π/ 2 , y (1)= 4 . |
|||||||||||
Получим 42 =16sin 2 π +C или 16 =16 +C . |
Отсюда C = 0 и, |
||||||||||
|
|
|
2 |
1 |
|
|
1 |
|
1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
следовательно, |
|
p2 =16sin 2 y , |
|
p = ± 16sin 2 y = ±4sin y . |
|||||||
Вернемся к исходной переменной |
y′ = ±4sin y . |
Воспользуемся |
|||||||||
начальными данными, чтобы выбрать знак. Из начальных данных
y(0)= π/ 2 , |
′ |
что |
нужно |
выбрать |
y (0)= 4 , следует, |
||||
положительный |
знак: y′ = 4sin y . |
Это |
уравнение |
первого |
18
порядка с разделяющимися переменными, запишем его в виде
|
|
dy |
= 4dx . |
|
|
|
|
|
|
|
|
|||
|
sin y |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Вычислим интеграл |
|
|
|
|
|
|
||||||
|
∫ |
dy |
|
|
= ∫ |
|
1 |
|
dy = lg |
|
tg(y / 2) |
|
. |
|
|
|
|
|
|
|
|
||||||||
|
sin y |
2sin(y / 2)(cos y / 2) |
||||||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
Получим |
tg(y / 2)= e4 x +C2 . |
Найдем константу, используя |
||||||||||
начальные данные: tg π = C2 , |
C2 |
=1 . Следовательно, решение |
||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
задачи Коши имеет вид tg y = e4 x +1. |
||||||||||||||
|
Ответ: |
tg y = e4 x +1. |
|
|
|
|
|
|
||||||
Задача 9
Найти общее решение дифференциального уравнения y(4) −3y′′′+3y′′− y′ = 3x2 + 2x +80.
Справочный материал
Уравнение вида
y(n) + a1 y(n−1) + a2 y(n−2) +... + an y = f (x)
является линейным уравнениям n -ого порядка с постоянными коэффициентами и специальной правой частью.
Общее решение такого уравнения имеет вид
yо.н. = уо.о. + уч.н. ,
то есть является суммой общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения.
Для нахождения общего решения однородного уравнения составляется характеристическое уравнение
19
λn +a1λn−1 +K+an−1λ+an = 0 .
Находятся корни характеристического уравнения. Каждому корню характеристического уравнения λi соответствует решение
вида yi = eλi x . Тогда общее решение однородного уравнения имеет вид:
y |
o.o. |
= C eλ1x +C |
2 |
eλ2 x +K+C |
n |
eλn x , |
|||
|
1 |
|
|
|
|
|
|||
или, в более общем виде: |
|
|
|
|
|
|
|
||
|
yo.o. = C1 y1 +C2 y2 +K+Cn yn . |
||||||||
Частное решение |
неоднородного |
|
уравнения уч.н. со |
||||||
специальной правой частью ищется методом подбора. |
|||||||||
В общем случае правая часть уравнения f (x) имеет вид |
|||||||||
специальный вид |
|
|
|
|
|
|
|
|
|
f (x) = eax (P (x) cos bx +Q |
n |
(x) sin bx) , |
|||||||
|
|
|
m |
|
|
|
|
|
|
где Pm ( x ), Qn ( x ) многочлены степени m и n соответственно. Частное решение неоднородного уравнения ищется в виде
yч.н. = x |
s |
e |
ax |
~ |
|
~ |
|
|
(Pk (x) cos bx |
+Qk (x) sin bx) . |
|||
Степень s равна кратности корня |
λm = a +ib характерис- |
|||||
|
|
~ |
~ |
многочлены степени k с |
||
тического уравнения, Pk |
(x), Qk (x) - |
|||||
неопределёнными коэффициентами, |
где k = max(m, n) . Таким |
|||||
образом, частное решение имеет тот же вид, что и правая часть уравнения, только многочлены записаны с неопределенными
коэффициентами. Они подбираются так, чтобы функция yч.н. была решением исходного уравнения.
Решение задачи 9
Исходное уравнение – линейное дифференциальное уравнение четвертого порядка с постоянными коэффициентами и
специальной правой частью f (x)= 3x2 + 2x +80.
20
Найдем сначала общее решение соответствующего однородного уравнения уо.о. :
y(4) −3y′′′+3y′′− y′ = 0.
Характеристическое уравнение имеет вид λ4 −3λ3 +3λ2 −λ = 0 ,
разложим левую часть уравнения на множители |
λ(λ −1)3 |
= 0 . |
||||||||||||||
Отсюда λ1 |
= 0 , |
λ2,3,4 =1 . Тогда общее решение имеет вид |
|
|||||||||||||
|
у |
о.о. |
= С +С |
2 |
ех |
+С |
3 |
хех +С |
4 |
х2 |
ех |
|
|
|||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
Правая |
часть |
исходного |
|
|
уравнения |
имеет |
вид |
|||||||||
f (x)= 3x2 |
+ 2x +80 , то есть содержит только многочлен. В этом |
|||||||||||||||
случае частное решение ищется в виде yч.н. |
= xs Qm (x) , где s – |
|||||||||||||||
кратность корня |
λ = 0 |
в характеристическом уравнении, а m – |
||||||||||||||
степень многочлена в правой части исходного уравнения. |
|
|||||||||||||||
В данном случае |
|
λ = 0 |
– |
|
корень |
характеристического |
||||||||||
уравнения |
кратности |
1, |
степень |
многочлена |
m = 2 , поэтому |
|||||||||||
частное решение исходного уравнения ищется в виде
yч.н. = x Q2 (x) = x ( Ax2 + Bx +C) = Ax3 + Bx2 +Cx.
Подставим его в исходное уравнение.
y(4) −3y′′′+3y′′− y′ = 3x2 + 2x +80.
Для этого сначала найдем
( yч.н. )′ = 3Ax2 + 2Bx +C
( yч.н. )′′ = 6Ax + 2B |
. |
|
( yч.н. )′′′ = 6A |
||
|
( yч.н. )(4) = 0
Получаем:
−18A +3(6Ax + 2B)−(3Ax2 + 2Bx +C)= 3x2 + 2x +80
или
−3Ax2 +(18A −2B)x +6B −18A −C = 3x2 + 2x +80 .
Приравняем коэффициенты при одинаковых степенях
21
|
− 3A = 3 |
|
|
A = −1 |
|
18A − 2B = 2 |
|
|
|
|
B = −10 |
|||
|
|
=80 |
|
|
6B −18A − C |
|
C = −102 |
||
следовательно, |
yч.н. |
= −x3 |
−10x2 −102x. |
|
Витоге общее решение исходного уравнения имеет вид
уо.н. = С1 +С2 ех +С3 хех +С4 х2 ех − х3 −10х2 −102х .
Ответ: у = С1 +С2 ех +С3 хех +С4 х2 ех − х3 −10х2 −102х.
Задача 10
Найти общее решение дифференциального уравнения y′′′−6 y′′+9 y′ = xe3x .
Справочный материал
Данное уравнение, как и уравнение в задаче 9, относится к линейным уравнениям более высокого порядка с постоянными коэффициентами и специальной правой частью. Метод решения таких уравнений описан выше в справочном материале к задаче 9. Отличие данной задачи заключается в том, что правая часть уравнения в задаче 10 имеет другой вид, а именно
f (x) = Pm (x) eαx . В этом случае частное решение ищется в
виде yч.н. = xs Qm (x) еαх , где s – кратность корня λ = α в характеристическом уравнении, а m – степень многочлена в правой части исходного уравнения. Если корень λ = α не является корнем характеристического уравнения, то s = 0 и
частное решение ищется в виде yч.н. = Qm (x) еαх
Решение задачи 10
Исходное уравнение является неоднородным линейным уравнением 3 порядка с постоянными коэффициентами. Правая
часть данного уравнения |
имеет специальный |
вид |
f (x) = P (x) eαx , а именно |
f (x)= xe3x . |
|
m |
|
|
22
Составим характеристическое уравнение |
λ3 −6λ2 +9λ = 0 , |
|||||||
разложим |
на |
множители |
λ (λ2 −6λ +9) = 0 |
или |
||||
λ (λ −3)2 |
= 0 . Найдем его корни λ = 0 , λ |
= 3 . |
|
|
||||
|
|
|
|
1 |
2,3 |
|
|
|
Таким |
образом, |
характеристическое |
уравнение |
|||||
λ3 −6λ2 +9λ = 0 |
имеет |
корень |
λ = 3 |
кратности |
2 и |
корень |
||
λ = 0 кратности 1. Поэтому решение однородного уравнения имеет вид:
yо.о. = С1 +С2 e3x +С3e3x x .
Найдем частное решение. Число λ = 3 является корнем кратности s=2, степень многочлена m =1, поэтому частное решение уравнения ищется в виде:
yч.н. = x2 ( Ax + B)e3x = Ax3e3x + Bх2 e3x
yч′.н. = 3e3x x2 A +3e3x x3 A + 2e3x xB +3e3x x2 B yч′′.н. = 6e3x xA +18e3x x2 A +9e3x x3 A + 2e3x B + +12e3x xB +9e3x x2 B
yч′′′.н. = 6e3x A +54e3x xA +81e3x x2 A + 27e3x x3 A + +18e3x B +54e3x xB + 27e3x x2 B.
Подставив y′, y′′, y′′′, в исходное уравнение получим:
6e3x A +54e3x xA +81e3x x2 A + 27e3x x3 A +18e3x B +
+54e3x xB + 27e3x x2 B −36e3x xA −108e3x x2 A −
−54e3x x3 A −12e3x B −
−72e3x xB −54e3x x2 B + 27e3x x2 A + 27e3x x3 A +
+12e3x xB +18e3x x2 B = xe3x .
Приведя подобные члены и сократив уравнение на e3x , получим 6А+ 6В +18Аx = x . Приравняем коэффициенты при одинаковых степенях x , получим 18A =1, A + B = 0 .Отсюда
A =1/18, B = −1/18 .
Общее решение исходного уравнения имеет вид.
23

yо.н. = С1 +С2 e3x +С3e3x x +181 e3x x3 −181 e3x x2 . Ответ: y = С1 +С2 e3x +С3e3x x +181 e3x x3 −181 e3x x2 .
Задача 11
Найти общее решение дифференциального уравнения
y''−9 y = e3x cos x .
Справочный материал
Метод решения уравнений такого типа описан выше в справочном материале к задаче 9. Правая часть уравнения в задаче 11 имеет другой вид, а именно
f (x) = eαx (a cosβx +bsin βx). В этом случае частное решение
ищется в |
виде |
yч.н. = xs |
еαх (Acosβx + B sin βx), |
где s – |
кратность |
числа |
λ = α +iβ |
в характеристическом |
уравнении. |
Если число λ = α +iβ не является корнем характеристического
уравнения, то s = 0 и частное решение ищется в виде yч.н. = еαх (Acosβx + B sin βx).
В некоторых вариантах экспонента отсутствует, то есть правая часть имеет вид f (x) = аcosβx +bsin βx . В этом случае
частное решение ищется в виде yч.н. = xs (Acosβx + B sin βx), где s – кратность числа λ = iβ в характеристическом уравнении, А и В – неопределенные коэффициенты. Если число λ = iβ не является корнем характеристического уравнения, то s = 0 и частное решение ищется в виде yч.н. = Acosβx + B sin βx .
Решение задачи 11
Исходное уравнение является неоднородным линейным уравнением 2 порядка с постоянными коэффициентами. Правая
24
часть данного |
уравнения имеет |
|
специальный |
вид |
||||
f (x) = eαx (a cosβx +bsin βx), а именно |
f (x)= e3x cos x |
|
||||||
Составим характеристическое |
уравнение λ2 −9 = 0 , |
его |
||||||
корни λ1 = 3 и λ2 = −3 . |
|
|
|
|
|
|
||
Следовательно |
y |
o.o. |
= C e3x |
+C |
2 |
e−3x . Найдем частное |
||
|
|
1 |
|
|
|
|
||
решение. Правая часть уравнения |
в нашем случае имеет вид |
|||||||
f (x)= e3x ( A cos x + B sin x) . Так как |
α = 3, β =1, число |
|||||||
α + β i = 3 +i не совпадает с корнями характеристического уравнения, следовательно s = 0 . Частное решение ищем в
виде |
yч.н. = e3x ( A cos x + B sin x) . Подставим его в |
исходное уравнение. |
|
yч′.н. |
= 3 e3x (A cos x + B sin x) +e3x (−A sin x + B cos x) = |
= e3x (3A cos x +3B sin x − A sin x + B cos x) , |
|
yч′′.н. |
= 3 e3x (cos x(B +3A) +sin x(3B − A)) + |
|
. |
+ e3x (−sin x(B +3A) + cos(3B − A)). |
|
Следовательно, |
|
e3x (cos x(3B +9A) +sin x(9B −3A)) + cos x(3B − A) − −sin x(B +3A) −9 e3x ( Acos x + B sin x) = e3x cos x
Приведем подобные члены в полученном выражении
cos x(3B +3B − A) +sin x(9B −3A − B −3A +9B) = cos x cos x(6B − A) +sin x(−6A − B) = cos x
Приравняем коэффициенты при cos x и sin x :
6B − A =1
6A + B = 0
25
|
Получим, A = −1/ 37, B = 6 / 37 . |
Тогда частное решение |
|||||||||||||||||
имеет вид |
yч.н. = e3x (− |
1 |
cos x + |
|
6 |
sin x) . |
|
|
|||||||||||
37 |
37 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
И наконец, общее решение исходное уравнения имеет вид |
||||||||||||||||||
y |
о.н. |
= c e3x + c |
2 |
e−3x + e3x ( |
6 |
sin x − |
1 |
cos x) . |
|||||||||||
|
|
|
|||||||||||||||||
|
1 |
|
|
|
|
37 |
|
|
37 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Ответ: |
y = c |
e3x + c |
2 |
e−3x + e3x |
( |
6 |
sin x − |
1 |
cos x) . |
|||||||||
|
|
|
|||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
37 |
|
|
37 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Задача 12
Найти общее решение дифференциального уравнения y′′+ 2 y′ = 3sin 2x +cos x .
Справочный материал
Данное уравнение, как и уравнения в задачах 9, 10, 11 относится к линейным уравнениям более высокого порядка с постоянными коэффициентами и специальной правой частью. Метод решения таких уравнений описан выше в справочном материале к задаче 9.
Особенность задачи 12 в том, что правая часть уравнения представляет собой сумму функций
f (x)= f1 (x) + f2 (x) +K+ fk (x) ,
каждая из которых, имеет специальный вид, рассмотренный в задачах 9, 10, 11. Решение заключается в следующем. Общее решение соответствующего однородного уравнения ищется аналогично, как и в задачах 9, 10, 11, а частное решение неоднородного уравнения ищется как сумма частных решений
yч.н. = yч1.н. + yч2.н. +K+ yчk.н.
Для нахождения этих частных решений исходное уравнение y(n) + a1 y(n−1) +... + an y = f1 (x) + f2 (x) +K+ fk (x)
Разбивается на совокупность k уравнений
26
y |
(n) + a |
y(n−1) +... + a |
n |
y = f |
i |
(x), i =1,K, k . |
|
|
|
||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для каждого из уравнений находится частное решение |
yчk.н. |
|
|||||||||||||||
|
|
|
|
|
Решение задачи 12 |
|
|
|
|
||||||||
|
|
Общее |
решение |
|
этого |
уравнения |
имеет |
вид |
|||||||||
yо.н. = yо.о. + yч1.н. + yч2.н. . |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
а) Решая однородное уравнение y′′+ 2 y′ = 0 , |
найдем yo.o. |
||||||||||||||
|
|
Характеристическое |
уравнение |
|
λ2 + 2λ = 0 . |
Его |
корни |
||||||||||
λ |
1 |
= 0, |
λ |
2 |
= −2, y |
o.o. |
= C +C |
2 |
e−2 x . |
|
|
|
|
||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||
|
|
б) |
Правая часть есть |
|
сумма |
двух |
функций |
||||||||||
f1 (x) = 3sin 2x, f2 (x) = cos x . |
|
|
Частное решение |
исходного |
|||||||||||||
уравнения будем искать в виде: |
|
yч.н. = yч1.н. + yч2.н. |
|
|
|||||||||||||
|
|
Найдем |
yч1.н. . Рассмотрим |
|
уравнение |
y′′+ 2 y′ = 3sin 2x , |
|||||||||||
здесь f1 (x) = 3sin 2x . В этой функции отсутствует экспонента и
присутствуют тригонометрическая функция sin 2x . Число 2i не является корнем характеристического уравнения, следовательно, s = 0 . Частное решение ищется в виде
yч1.н. = Asin 2x + B cos 2x.
Определим значения коэффициентов A и B . Вычислим производные функции yч1.н. :
yч1.н. = Asin 2x + B cos 2x. (yч1.н. )′ = 2Acos 2x − 2B sin 2x.
(yч1.н. )″ = −4Asin 2x −4B cos 2x.
Подставим значения y′ и y′′ в исходное уравнение
−4Asin 2x −4B cos 2x + 4 Acos 2x − 4B sin 2x = 3sin 2x .
Приравнивая коэффициенты при cos 2x и sin 2x в правой и
27

левой части уравнения, получим систему для определения коэффициентов A и B :
− 4A − 4B = 3
− 4B + 4A = 0 .
Отсюда A = −3 / 8, B = −3/8 . Следовательно
|
|
|
|
|
yч1.н. = − |
3 sin 2x − |
3 cos 2x. |
|
|
|||
|
|
|
|
|
|
8 |
|
|
8 |
|
|
|
|
Найдем |
yч2.н. . Рассмотрим уравнение y′′+2y′=cos x . Здесь |
||||||||||
f2 (x) = cos x . |
В этой функции отсутствует экспонента, поэтому |
|||||||||||
a = 0 . |
В |
этой функции |
присутствуют |
тригонометрическая |
||||||||
функция cos x , поэтому b =1. |
Составим |
a +bi = i . |
Число i |
|||||||||
не |
является |
корнем |
|
характеристического |
уравнения, |
|||||||
следовательно, |
s = 0 . |
|
|
|
|
|
|
|
||||
|
Частное решение ищем в виде yч2.н. = Asin x + B cos x. |
|||||||||||
|
Найдем |
|
неопределённые |
коэффициенты. |
|
Вычислим |
||||||
производные этой функции. |
|
|
|
|
|
|
||||||
|
yч2.н. |
= Asin x + B cos x. |
|
|
|
|
|
|
|
|||
|
(yч2.н. )′ = Acos x − B sin x. |
|
|
|
|
|
|
|||||
|
(yч2.н. )″ = − Asin x − B cos x. |
|
|
|
|
|
||||||
|
Подставляя |
значения |
y′ |
и y′′ |
в исходное |
уравнение и |
||||||
приравнивая |
коэффициенты |
|
при |
cos x |
и sin x , |
найдем: |
||||||
A = 2 / 5, B = −1/5 .
yч2.н. = 52 sin x − 15 cos x.
Правая часть представляет собой сумму двух функций, поэтому частное решение будем искать в виде:
yч.н. = yч1.н. + yч2.н.
yч.н. = − 83 sin 2x − 83 cos 2x + 52 sin x − 15 cos x.
28

|
|
Отсюда |
|
|
|
− 3 sin 2x − 3 cos 2x + |
2 |
|
|
1 |
|
|
|||||||
|
|
y |
o.н. |
= C +C |
e−2 x |
sin x − |
cos x. |
||||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
1 |
2 |
|
|
8 |
8 |
5 |
|
|
5 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Ответ: |
y = C +C |
2 |
e−2 x |
− 3 sin 2x − 3 cos 2x + |
2 |
sin x − |
1 |
cos x. |
|||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
1 |
|
|
8 |
8 |
5 |
|
5 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
Задача 13 |
|
|
|
|
|
|
|
|
|
|
|
Найти решение задачи Коши. |
|
|
|
|
|
|
|
|
|
||||||||
|
′′ |
|
|
|
|
1 |
|
|
|
′ |
|
|
|
|
|
|
|
|
|
y |
+ y = cos x |
, |
|
|
=1. |
|
|
|
|
|
|
|
|
||||||
|
|
y(0) = 0, y (0) |
|
|
|
|
|
|
|
|
|||||||||
Справочный материал
Для решения таких уравнений применяется метод Лагранжа. Сначала ищется общее решение соответствующего однородного уравнения. Для нахождения общего решения сначала ищутся корни характеристического уравнение. Тогда общее решение однородного уравнения имеет вид:
yo.o. = C1 y1 +C2 y2 .
Общее решение неоднородного уравнения ищется в виде y = C1 (x) y1 +C2 (x) y2 ,
гдеC1 (x),C2 (x) - некоторые неизвестные функции.
Система для нахождения неизвестных функций имеет вид
|
y C′ + y C′ |
= 0, |
|
|||
|
′ 1 ′ |
1 |
′ 2 ′ |
2 |
|
. |
y1C1 |
+ y2C2 |
= f (x) |
|
|||
Разрешая эту систему относительно Сi′(x),i =1,2 , получаем
dCi = ϕi (x), i =1,2 , dx
Откуда
29
~ |
|
Ci (x) = ∫ϕi (x)dx +Ci , i =1,2 , |
|
где С~i - произвольные постоянные. |
|
Тогда y = C1 (x) y1 +C2 (x) y2 есть общее |
решение |
уравнения. |
|
Решение задачи 13 |
|
Соответствующее однородное уравнение будет y′′+ y = 0 . |
|
Его характеристическое уравнениеλ2 +1 = 0 имеет |
мнимые |
корни λ1 = −i , λ2 = i и общее решение однородного уравнения имеет вид
yo.o. (x) = C1 cos x +C2 sin x .
Общее решение неоднородного уравнения ищем в виде y = C1 (x) cos x +C2 (x)sin x ,
где C1 (x), C2 (x) - неизвестные функции от х. Для их нахождения составим систему
|
cos x C′(x) +sin x C |
′ |
(x) = 0, |
|||
|
1 |
2 |
|
1 . |
||
|
|
|
|
|||
−sin x C1′(x) + cos x C2′ |
(x) = |
|
|
|||
cos x |
||||||
|
|
|
|
|||
Разрешаем эту систему относительно С1′(x) и C2′(x) :
C1′(x) = −tgx ; C2′(x) =1, |
~ |
|
|
|
|
|
||||||||||||||||||||
находим С1 (x) = ln |
|
cos x |
~ |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
+C1 , C2 (x) |
= x +C2 . |
|
|
||||||||||||||||||||||
Таким образом, общее решение данного уравнения |
||||||||||||||||||||||||||
|
|
~ |
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
cos x |
|
|
+ x sin x . |
||||
|
y = C1 cos x +C2 sin x +cos x ln |
|
|
|||||||||||||||||||||||
|
~ |
~ |
|
sin x + cos x ln |
|
cos x |
|
+ x sin x |
|
|||||||||||||||||
y = C cos x +C |
2 |
|
|
|
||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
~ |
|
|
cos x −sin x ln |
|
cos x |
|
|
+ x cos x |
|||||||||||||||
y′ = −C |
sin x +C |
|
|
|
|
|
||||||||||||||||||||
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Начальные данные имеют вид y(0) = 0, |
||||||||||||||||||||||
Решим задачу Коши. |
||||||||||||||||||||||||||
′ |
|
Подставим в систему x = 0 |
, y = 0 , y |
′ |
= 0 получим |
|||||||||||||||||||||
y (0) =1. |
|
|||||||||||||||||||||||||
С~ |
= 0, С~ |
=1. Ответ: |
y = sin x + сosx ln |
|
cos x |
|
+ x sin x . |
|||||||||||||||||||
|
|
|||||||||||||||||||||||||
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30

Вариант №1.
1.Найти общий интеграл дифференциального уравнения. (Ответ представить в виде ψ(x, y) = C ).
4xdx −3ydy = 3x 2 ydy −2xy2dx .
2. |
Найти решение задачи Коши. |
y′− |
y |
= x 2 , y(1) |
= 0 . |
3. |
x |
||||
Найти решение задачи Коши. |
|
|
|
|
|
|
y2dx +(x +e2 / y )dy = 0, |
y(e) = 2 . |
|
||
4.Найти общий интеграл дифференциального уравнения.
3x2eydx + (x3ey −1)dy = 0 .
5.Методом изоклин построить интегральную кривую, походящую через точку М. y′ = y − x 2 , М (1; 2).
6.Найти линию, проходящую через точку M0 и обладающую тем
→
свойством, что в любой ее точке М нормальный вектор MN
с концом на оси ОY имеет длину, равную а и образует острый угол с положительным направлением оси ОY. M0 (15; 1), a = 25 .
7.Найти общее решение дифференциального уравнения.
y′′′x ln x = y′′.
8.Найти решение задачи Коши.
4y3 y′′= y4 −1, y(0) =  2, y′(0) =1/(2
2, y′(0) =1/(2  2) .
2) .
9.Найти общее решение дифференциального уравнения.
y′′′+3y′′+ 2y′ =1 − x3 .
10.Найти общее решение дифференциального уравнения.
y′′′−4y′′+5y′−2y = (16 −12x)e−x .
11.Найти общее решение дифференциального уравнения.
y′′+ 2y′ = 4ex (sin x + cos x) .
12.Найти общее решение дифференциального уравнения.
y′′−2y′ = 2ch2x .
13.Найти решение задачи Коши.
|
′′ |
|
2 |
|
π2 |
|
′ |
|
y |
+ π |
|
y = cos πx , |
= 0 . |
||||
|
|
y(0) = 3, y (0) |
||||||
31
.
.
.
.
.
.
.
.
.
Вариант №2.
1Найти общий интеграл дифференциального уравнения. (Ответ представить в виде ψ(x, y) = C ).
x 1 + y2 + yy′ 1 + x 2 = 0 .
1 + x 2 = 0 .
2 |
Найти решение задачи Коши. |
|
|
||||||
|
y′− yctgx = 2x sin x, |
y(π 2) = 0 . |
|||||||
3 |
Найти решение задачи Коши. (y4ey + 2x)y′ = y, y(0) =1. |
||||||||
4 |
Найти общий интеграл дифференциального уравнения. |
||||||||
|
(3x 2 + |
2 |
cos |
2x |
)dx = |
2x |
cos |
2x |
dy . |
|
|
|
|
|
|||||
|
|
y |
y |
y2 |
y |
||||
5Методом изоклин построить интегральную кривую, походящую через точку М. yy′ = −2x, М (0; 5).
6Найти линию, проходящую через точку M0 и обладающую тем
→
свойством, что в любой ее точке М нормальный вектор MN
с концом на оси ОY имеет длину, равную а и образует острый угол с положительным направлением оси ОY. M0 (12; 2), a = 20 .
7 Найти общее решение дифференциального уравнения.
xy′′′+ y′′ =1.
8 Найти решение задачи Коши.
y′′ =128y3 , y(0) =1, y′(0) = 8 .
9 Найти общее решение дифференциального уравнения.
y′′′− y′′ = 6x 2 +3x .
1Найти общее решение дифференциального уравнения.
0.y′′′−3y′′+ 2y′ = (1 − 2x)ex .
1Найти общее решение дифференциального уравнения.
1.y′′−4y′+ 4y = −e2x sin 6x .
1Найти общее решение дифференциального уравнения.
2. |
y′′+ y = 2sin x −6 cos x + 2e x . |
|
|
||||||
3. |
1 Найти решение задачи Коши. |
|
|
||||||
|
′′ |
|
′ |
|
9e3x |
|
′ |
|
|
|
y |
+3y |
= 1 + e3x , y(0) = ln 4, |
= 3(1 −ln 2) . |
|||||
|
|
|
y (0) |
||||||
32

.
.
.
Вариант №3.
1 Найти общий интеграл дифференциального уравнения. (Ответ представить в виде ψ(x, y) = C ). 4 + y2 dx − ydy = x 2 ydy .
2 Найти решение задачи Коши.
|
′ |
1 |
|
|
y |
+ y cos x = 2 sin 2x, y(0) |
= 0 . |
||
|
3 Найти решение задачи Коши.
y2dx +(xy −1)dy = 0, y(1) = e .
4 Найти общий интеграл дифференциального уравнения.
. |
(3x 2 + 4y2 )dx +(8xy +ey )dy = 0 . |
|
5 Методом изоклин построить интегральную кривую, походящую через |
.
.
.
.
.
точку М. y′ = 2 + y2 , М (1; 2).
6 Найти линию, проходящую через точку M0 и обладающую тем
→
свойством, что в любой ее точке М нормальный вектор MN
с концом на оси ОY имеет длину, равную а и образует острый угол с положительным направлением оси ОY. M0 (9; 3), a =15 .
7 Найти общее решение дифференциального уравнения.
2y′′′x = y′′.
8 Найти решение задачи Коши.
y′′y3 +64 = 0, y(0) = 4, y′(0) = 2 .
9 Найти общее решение дифференциального уравнения.
y′′′− y′ = x 2 + x .
1Найти общее решение дифференциального уравнения.
0.y′′′− y′′− y′+ y = (3x +7)e2x .
1Найти общее решение дифференциального уравнения.
1.y′′+ 2y′ = −2ex (sin x +cos x) .
1Найти общее решение дифференциального уравнения.
2.y′′′− y′ = 2ex +cos x .
1Найти решение задачи Коши.
3. |
y |
′′ |
+ 4y |
= 8ctg2x, |
y( |
π |
′ |
π |
|
|
4 ) = 5, y ( |
4 ) = 4 . |
|||||
33

.
.
.
.
.
.
.
.
.
0.
Вариант №4.
1 Найти общий интеграл дифференциального уравнения. (Ответ
|
представить в виде ψ(x, y) = C ). |
|
3 + y2 dx − ydy = x 2 ydy . |
|||||||||
2 |
|
|
|
|
|
′ |
|
2 |
π 1 |
|||
|
|
|
|
|
|
|
|
|
|
|
||
3 |
Найти решение задачи Коши. y |
+ ytgx |
= cos x, y( 4 ) = 2 . |
|||||||||
|
||||||||||||
Найти решение задачи Коши. 2(4y2 + 4y − x)y′ =1, |
y(0) = 0 . |
|||||||||||
4 |
Найти общий интеграл дифференциального уравнения. |
|
|
|
||||||||
|
(2x −1 − |
y |
)dx −(2y − |
1 |
)dy = 0 . |
|
|
|
|
|||
|
x 2 |
|
|
|
|
|
||||||
|
|
|
x |
|
|
|
|
|
|
|||
5 Методом изоклин построить интегральную кривую, походящую через
|
точку М. y′ = |
2x |
|
|
|
|||
|
|
, |
М (1; 1). |
|
||||
|
3y |
|
||||||
6 |
Найти линию, проходящую через точку M0 и обладающую тем |
|||||||
|
|
|
|
|
|
|
|
→ |
|
свойством, что в любой ее точке М нормальный вектор MN |
|||||||
|
с концом на оси ОY имеет длину, равную а и образует острый угол с |
|||||||
|
положительным направлением оси ОY. M0 (6; 4), a =10 . |
|||||||
7 |
Найти общее решение дифференциального уравнения. |
|||||||
|
xy′′′+ y′′ = x +1. |
|
||||||
8 |
Найти решение задачи Коши. |
|
||||||
|
y |
′′ |
+ 2sin y cos |
3 |
y = 0, |
′ |
||
|
|
|
y(0) = 0, y (0) =1 . |
|||||
9 Найти общее решение дифференциального уравнения.
y′′′−3y′′+3y′− y = 2x .
1Найти общее решение дифференциального уравнения.
. y′′′−2y′′+ y′ = (2x +5)e2x
1Найти общее решение дифференциального уравнения.
1.y′′+ y = 2 cos 7x +3sin 7x .
1Найти общее решение дифференциального уравнения.
2.y′′−3y′ = 2ch3x .
1Найти решение задачи Коши.
3. |
′′ |
−6y |
′ |
+8y = |
4 |
, |
′ |
= 6 ln 2 . |
|
y |
1 + e−2x |
||||||||
|
|
y(0) =1 + 2 ln 2, y (0) |
34

.
.
.
.
.
.
.
.
.
Вариант №5.
0Найти общий интеграл дифф. уравнения. (Ответ представить в виде
1ψ(x, y) = C ). 6xdx −6ydy = 2x 2 ydy −3xy2dx .
2 |
Найти решение задачи Коши. y′− |
y |
= x |
2 |
+ 2x, y(−1) |
= |
3 |
. |
|
|
x + 2 |
|
2 |
||||||
3 |
Найти решение задачи Коши. |
|
y(1 4)= π 3 . |
|
|
|
|||
|
(cos 2 y cos2 y − x) y′ = sin y cos y, |
|
|
|
|||||
4 Найти общий интеграл дифференциального уравнения.
(y2 + y sec2 x)dx +(2xy + tgx)dy = 0 .
5 Методом изоклин построить интегральную кривую, походящую через
точку М. y′ = (y −1)x, M(1; 3/2).
6 Найти линию, проходящую через точку M0 и обладающую тем
→
свойством, что в любой ее точке М нормальный вектор MN с концом на оси ОY имеет длину, равную а и образует острый угол с положительным
направлением оси ОY. M0 (3; 5), a = 5 .
7 Найти общее решение дифференциального уравнения.
y′′tgx − y′+ sin1 x = 0 .
8 Найти решение задачи Коши.
y′′ = 32sin3 y cos y, y(1) = π/ 2, y′(1) = 4 .
9 Найти общее решение дифференциального уравнения.
y1V − y′′′ = 5(x + 2)2 .
1Найти общее решение дифференциального уравнения.
0.y′′′−3y′′+ 2y′ = (18x −21)e−x .
1Найти общее решение дифференциального уравнения.
1.y′′+ 2y′+5y = −sin 2x .
1Найти общее решение дифференциального уравнения.
2.y′′+ 4 y = −8sin 2x + 32cos 2x + 4e2x .
1Найти решение задачи Коши.
3. |
′′ |
−9y |
′ |
+18y = |
9e3x |
|
′ |
= 0 . |
|
y |
1 + e3x , |
||||||||
|
|
y(0) = 0, y (0) |
|||||||
35
