7. Вычисление длины дуги

1. Пусть дуга AB кривой задана уравнением , где  непрерывно дифференцируемая функция. Тогда длина дуги AB

. (5.14)

2. В случае, когда кривая задана параметрическими уравнениями , , где  непрерывно дифференцируемые функции, длина дуги вычисляется по формуле

. (5.15)

Здесь α, β  значения параметра t, соответствующие концам дуги AB.

3. Если гладкая кривая задана в полярных координатах уравнением , то длина l дуги AB вычисляется по формуле

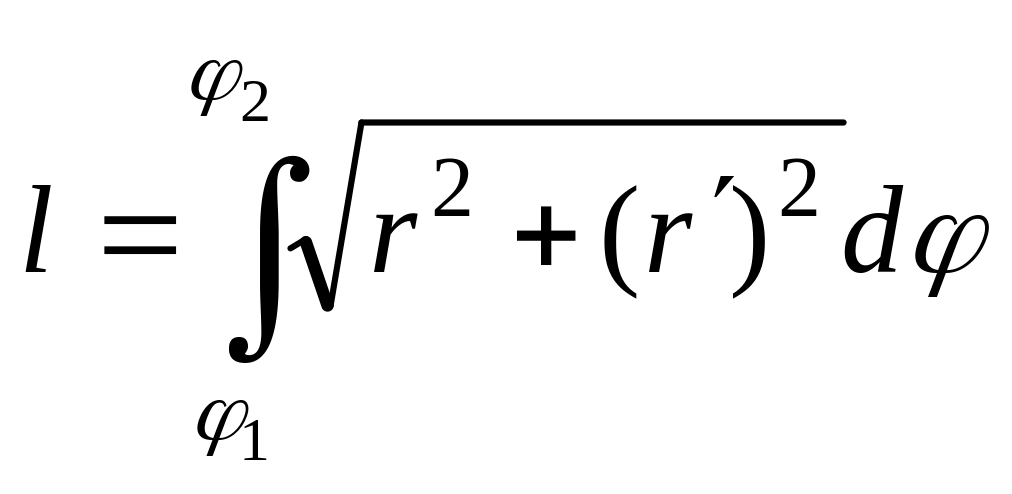, (5.16)

где и соответствуют концам дуги AB.

8. Пусть криволинейная трапеция, ограниченная прямыми линиями , и частью графика кривой , вращается вокруг оси . Тогда объем полученного при этом тела вращения вычисляется по формуле

. (5.17)

Пример 1. Найти .

▲ Используя формулы (5.1), имеем

.

Проверка. .▼

Пример 2. Найти .

▲ Применяя (5.2), получим

.▼

Пример 3. Найти .

▲ Применяя формулу (5.3), имеем

. ▼

Пример 4. Найти .

▲

.

Перенося последний интеграл в левую часть равенства, получим

.

Следовательно, . ▼

Пример 5. Найти .

▲ Рациональная подынтегральная дробь является правильной (см. методы интегрирования 4) и разлагается на простейшие дроби вида (5.4):

.

Если привести дроби из данного разложения к общему знаменателю, то он совпадает со знаменателем исходной подынтегральной функции. Числители в левой и правой частях последнего равенства будут тождественно равными, т.е.

.

Для нахождения неизвестного коэффициента A используем метод частных значений, т. е. подставим вместо переменной x ее частное значение, совпадающее с вещественным корнем знаменателя, . Получим равенство , откуда следует, что .

Для вычисления значений M, N используем метод неопределенных коэффициентов. Приравнивая коэффициенты при одинаковых степенях x в обеих частях полученного тождества, получаем систему уравнений

Решение этой системы: . Таким образом,

. ▼

Пример 6. Найти .

. ▲

Пример 7. Вычислить несобственные интегралы или установить их расходимость: .

▲ 1) Первый интеграл является несобственным интегралом с бесконечным верхним пределом интегрирования. Согласно определению (5.9), имеем

.

2) Второй интеграл является несобственным интегралом от неограниченной функции; функция терпит бесконечный разрыв в нижнем пределе . Согласно определению (5.10) получаем

.

Оба несобственных интеграла сходятся. ▼

Пример 8. Вычислить площадь фигуры, ограниченной линиями и .

▲ Находим точки пересечения данных кривых:

у

2

х

−2 −1 O 1 2 3 4

−2

−4

Рис.8

Следовательно, по формуле (5.11) имеем (см. рис. 8)

. ▼

Пример 9. Вычислить длину одной арки циклоиды

, .

▲ Поскольку все арки циклоиды одинаковы, рассмотрим ее первую арку, вдоль которой параметр t изменяется от 0 до 2 (см. рис. 9). Тогда, согласно формуле (5.15), имеем ,

у

2

О 2 4 6 х

Рис. 9

. ▼

Пример 10. Вычислить объем тела, образованного вращением вокруг оси кривой .

▲ Объем полученного тела вращения найдем по формуле (5.17):

. ▼

После изучения темы ”Неопределенный и определенный интеграл“ выполните контрольную работу 5.