
«Дополнительные главы ТОЭ» Лекция 4
Расчет цепи при действии последовательности импульсов.
Разностные уравнения.
Доцент ВШВЭ Е.Ю.Кочеткова
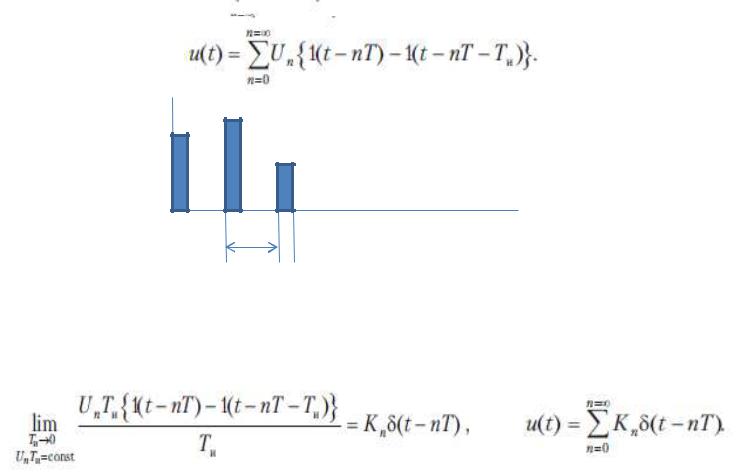
Последовательность прямоугольных импульсов с амплитудами Un = {U0 ,U1 , U2 ….} и длительностью Ти :
u U0
t
Т  Ти
Ти
Если Ти → 0: последовательность δ - импульсов
Kn - площадь n –го импульса

Решетчатые функции
Решетчатая функция – последовательность дискретных значений функции f(t) в моменты времени 0, Т, 2Т,….
Пример 1 |
U[n] = U0 - решетчатая |
U |
константа |
u(t) |
|
|
|
|
|
|
|
|
|
|
U0 |
|
|
|
|
|
|
|
U0 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
t |
|
n |
|
|
|
|
|
|
|||||
0 |
T 2T 3T |
0 1 |
2 3 |
|||||||
Пример 2 |
|
|
|
|
|
|
|
|
|
|
f [n] e anT |
решетчатая экспонента |
|
|
|||||||
Разностные уравнения
Аналогом дифференциального уравнения, которое описывает процессы при действии непрерывных сигналов, является разностное уравнение, которое описывает процессы при воздействии импульсов. Разностное уравнение связывает значения решетчатой функции в отдельные моменты времени.
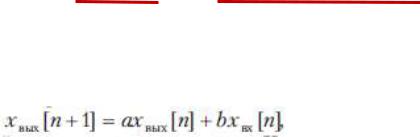
Разностное уравнение 1-го порядка устанавливает связь между значением выходного сигнала в начале (n+1) –го интервала со значением в начале n-го интервала.
Формирование разностного уравнения 1-го порядка. Пусть на вход цепи действует последовательность прямоугольных импульсов длительностью Ти : xвх [n]
Значение xвых [n+1] можно получить методом наложения двух процессов:
1-й процесс определяется энергией, накопленной к началу n-го интервала (к моменту nT), 2-й процесс определяется только действием импульса, который пришел в момент nT
xвых [n+1] = xвых [n] e-T/τ + xвх [n] ( h(T) – h(T - Ти) )
1 |
2 |
Общий вид разностного уравнения 1-го порядка:
где α = e-T/τ , b = h(T) – h(T - Ти) , h - переходная характеристика цепи
Аналитическое решение разностного уравнения можно получить способом, схожим с классическим методом расчета переходных процессов:
xвых [n] = xвых’[n] + xвых”[n] ,
где xвых’[n] – частное решение неоднородного разностного уравнения, xвых”[n] – общее решение однородного разностного уравнения
xвых [n+1] - α xвых [n] = 0

Пример.
Расчет rL-цепи, находящейся под воздействием прямоугольных импульсов с амплитудой U0 и длительностью Тu.
|
-T/τ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
Y (t) |
1 |
|
t |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
e |
|
||||
i[n+1] = i[n] e |
+ u[n] ( Y(T) – Y(T - Ти) ), |
u[n]=U |
|
r |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При t→∞ i[n+1]=i[n], подставляя в уравнение, находим i’[n]: |
|
|
|
|
||||||||||||||||||||
|
i'[n] |
bu[n] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где α = e-T/τ , b = Y(T) – Y(T - Ти) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Однородное уравнение: i[n+1] -i[n] e-T/τ = 0 |
|
|
|
|
|
|
|
|
||||||||||||||||
Характеристическое уравнение: λ - e-T/τ = 0, λ = e-T/τ , i”[n] =C λn |
|
|
||||||||||||||||||||||
C определим из начальных условий i[0]=0 |
|
|
|
|
|
|
|
|
||||||||||||||||
0=i' [0]+C |
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U0 |
|
e |
|
|
|
|
Tu |
|
|
|
nT |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Решение: |
i[n] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
r |
|
|
|
|
|
T |
|
e |
|
|
1 1 e |
|
|
|
|
|
|
|
||||
|
|
|
|
|
1 e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
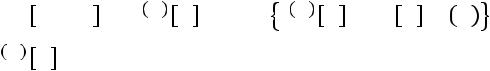
Формирование разностного уравнения 1-го порядка при воздействии на входе цепи последовательности δ- импульсов площадью К [n] (на примере rL- цепи )
Состояние цепи перед приходом очередного δ- импульса и сразу после δ- импульса отличаются, хотя и относятся к одному и тому же моменту nT .
Обозначим
|
i |
( ) |
[n] |
|
|
|
|
||
i |
( ) |
[n] |
||
|
|
|||
значение тока до прихода импульса в момент nT,
значение тока после прихода импульса в момент nT
(+)[ ] = (−)[ ] + [ ] (0)
Перед приходом следующего δ- импульса в момент (n+1)T
(−) + 1 |
= + |
− |
− |
|
|
− |
|
= |
|
+ 0 |
= |
(*) |
|||
|
|
|
|
|
|
|
−
−
+ K[n] (T)
После прихода δ- импульса в момент (n+1)T |
|
|
|||||
|
|
|
T |
|
|
(**) |
|
i( )[n 1] i( )[n 1] K[n 1]Y |
(0) i( )[n]e |
|
K[n 1]Y (0) |
||||
|
|
||||||
|
|
|
|
|
|
|
|

Таким образом , получены два разностных уравнения: в уравнении (*) дискретный момент времени nT – это момент, предшествующий приходу импульса, а в уравнении (**) дискретный момент времени nT – это момент, следующий за приходом импульса.
Для примера используем уравнение (**):
|
|
|
|
|
|
T |
|
i[n 1] i[n]e |
|
||||||
|
|||||||
|
|
||||||
|
|
1 |
|
t |
|
|
|
Y |
(t) |
|
|
|
|||
|
e |
|
|
||||
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
||
K[n 1]Y (0)
Y (0) |
1 |
|
|
|
L |
|
Аналитическое решение разностного уравнения можно получить, как i [n] = i’[n] + i”[n] ,
где i’[n] – частное решение неоднородного разностного уравнения, i”[n] – общее решение однородного разностного уравнения
Пусть K[n]=K =const
При t→∞ i[n+1]=i[n], подставляя в уравнение, находим i’[n]:

i'[n] |
K |
|
1 |
L |
|
|
|
|
1 |
e |
|
|
|
T
Однородное уравнение: i[n+1] - i[n] e-T/τ =0
Характеристическое уравнение: λ - e-T/τ = 0, λ = e-T/τ , i”[n] =C λn
C определим из начальных условий: i[0] = KYδ (0) = K/L
K/L =i' [0]+C = i' [n]+C
C = K/L - i' [n]
Решение
|
|
|
|
|
|
( n 1)T |
|
|||
i[n] |
K 1 e |
|
|
|
|
|
||||
|
|
|
|
|
|
|||||
L |
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
e |
|
|
||||||
|
|
|
|
|||||||
«Дополнительные главы ТОЭ» Лекция 5
Расчет цепи при действии последовательности импульсов.
Z-преобразование
Доцент ВШВЭ Е.Ю.Кочеткова
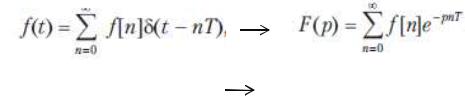
Расчет реакции цепи при воздействии последовательности
импульсов с помощью z- преобразования.
Аналогия:
Операторный метод – для непрерывных функций времени, Метод z- преобразования – для решетчатых функций.
Схема метода:
1. Переход от решетчатой функции f[n] к ее z-изображению F(z). 2. Решение задачи для z-изображений.
3. Переход к оригиналу: искомой решетчатой функции.
Преобразование, определяющее соответствие решетчатой функции f[n] и ее z- изображения F(z), можно найти, вычисляя операторное изображение функции, описывающей последовательность δ-импульсов площадью f[n] :
Обозначим
z e |
pT |
e |
T |
e |
j T |
|
|
|
|
n |
|
F (z) f [n]z |
||
|
||
n 0 |
|
f[n] 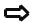 F(z)
F(z)
Условие сходимости z- преобразования: если f[n] |
при n→∞ растет не быстрее e 0 nT |
то ряд F(z) сходится вне круга с радиусом R e 0T |
0 |
