Билеты 2021 / билет

http://www.rec.vsu.ru/rus/ecourse/eldin/sto.pdf

https://scask.ru/c_book_t_phis2.php?id=77 – книга где есть всё

8) Тензор электромагнитного поля. Преобразование напряженностей поля.0

9) Уравнения Максвелла в четырехмерной форме. Действие и лагранжиан электромагнитного поля.

10) Уравнения Максвелла в трехмерном виде и их физическое содержание. Интегральная и дифференциальная формы уравнений Максвелла.

---------Интегральная---------

11) Сохранение заряда и уравнение непрерывности. Плотность заряда и плотность тока при дискретном и непрерывном описании распределения зарядов.

Из 3 закона Максвела:

Дискретный?

12) Потенциалы электромагнитного поля и калибровочная инвариантность электродинамики. Условие Лоренца.

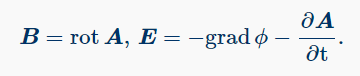
Магнитный поток (Ф):

13) Уравнение Пуассона. Потенциал и напряженность электростатического поля.

14) Поле стационарных токов. Закон Био - Савара.

Из колибровки лоренса можно:

15) Прецессия магнитного момента в магнитном поле. Теорема Лармора.

16) Монохроматическая плоская волна.

17) Поле произвольно движущихся зарядов. Запаздывающие потенциалы.

18) Поле системы движущихся зарядов на большом расстоянии от системы. Излучение волн.

19) Дипольное излучение. Излучение медленно движущихся зарядов.

20) Квадрупольное и магнито-дипольное излучение.

21) Торможение излучением.

В § 65 было показано, что разложение потенциалов поля системы зарядов в ряд по степеням   приводит во втором приближении к функции Лагранжа, вполне определяющей (в этом приближении) движение зарядов. Произведем теперь разложение поля до членов более высокого порядка и выясним, к каким эффектам приводят эти члены. В разложении скалярного потенциала

член третьего порядка по 1/с равен

По тем же причинам, что и при выводе (65,3), в разложении векторного потенциала мы должны взять только член второго порядка по 1/с, т. е.

Произведем преобразование потенциалов:

выбрав функцию f таким образом, чтобы скалярный потенциал   обратился в нуль:

Тогда новый векторный потенциал будет равен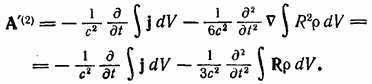

Переходя здесь от интегралов к суммам по отдельным зарядам, для первого слагаемого в правой части получим выражение —  . Во втором слагаемом пишем  , где   имеют обычный смысл (см. § 66); тогда  , и второе слагаемое принимает вид  . Таким образом,

Соответствующее этому потенциалу магнитное поле равно нулю  )   поскольку   не содержит явным образом координат. Электрическое же поле,   равно

где d — дипольный момент системы.

Таким образом, члены третьего порядка в разложении поля приводят к появлению дополнительных действующих на заряды сил, не содержащихся в функции Лагранжа (65,7); эти силы зависят от производных по времени от ускорения зарядов.

Рассмотрим систему зарядов, совершающих стационарное движение и вычислим среднюю работу, производимую полем (75,4) за единицу времени. На каждый заряд   действует сила  , т. е.

В единицу времени эта сила производит работу, равную  ; полная работа, совершенная над всеми зарядами, равна сумме по зарядам:

При усреднении по времени первый член исчезает, так что средняя работа оказывается равной

Но стоящее справа выражение есть не что иное, как (взятое с обратным знаком) среднее излучение энергии системой за единицу времени (см. (67,8)). Таким образом, возникающие в третьем приближении силы (75,5) описывают обратное действие излучения на заряды. Эти силы носят название торможения излучением или лоренцевых сил трения.

Одновременно с потерей энергии в излучающей системе зарядов происходит также и потеря момента импульса. Уменьшение момента импульса в единицу времени, , легко вычислить с помощью выражений для сил торможения. Дифференцируя момент  по времени, имеем , так как . Производную по времени от импульса частицы заменяем действующей на нее силой трения (75,5) и находим:

Нас интересует среднее по времени значение потери момента импульса при стационарном движении, подобно тому как выше нас интересовала средняя потеря энергии. Написав

и замечая, что полная производная по времени (первый член) при усреднении исчезает, найдем окончательно следующее выражение для средней потери момента импульса излучающей системой:

Торможение излучением имеет место и при наличии одного движущегося во внешнем поле заряда. Оно равно

Для одной частицы можно всегда выбрать такую систему отсчета, в которой она в данный момент времени покоится. Если вычислять в такой системе дальнейшие члены разложения создаваемого зарядом поля, то легко убедиться в том, что при стремлении к нулю радиус-вектора R от заряда к точке наблюдения все эти члены обращаются в нуль. Таким образом, в случае одного заряда формула (75,8) является точным выражением для обратного действия излучения в той системе отсчета, в которой заряд покоится.

Надо, однако, иметь в виду, что описание действия заряда «самого на себя» с помощью силы торможения вообще не является вполне удовлетворительным и содержит в себе противоречия. Уравнение движения заряда в отсутствие внешнего поля, на который действует только сила (75,8), имеет вид

Это уравнение имеет, кроме тривиального решения  , еще решение, в котором ускорение v пропорционально  , т. е. неограниченно возрастает со временем. Это значит, например, что заряд, прошедший через какое-нибудь поле, по выходе из поля должен был бы неограниченно «само-ускоряться». Абсурдность этого результата свидетельствует об ограниченной применимости формулы (75,8).

Может возникнуть вопрос о том, каким образом электродинамика, удовлетворяющая закону сохранения энергии, может привести к абсурдному результату, в котором свободная частица неограниченно увеличивает свою энергию. Корни этой трудности находятся, в действительности, в упоминавшейся ранее (§ 37) бесконечной электромагнитной «собственной массе» элементарных частиц. Когда мы пишем в уравнениях движения конечную массу заряда, то мы этим, по существу, приписываем ему формально бесконечную же отрицательную «собственную массу» неэлектромагнитного происхождения, которая вместе с электромагнитной массой приводила бы к конечной массе частицы. Поскольку, однако, вычитание одной из другой двух бесконечностей не является вполне корректной математической операцией, то это и приводит к ряду дальнейших трудностей, в том числе и к указанной здесь.

В системе координат, в которой скорость частицы мала, уравнение движения с учетом торможения излучением имеет вид

По изложенным соображениям, это уравнение применимо только постольку, поскольку сила торможения мала по сравнению с силой, действующей на заряд со стороны внешнего поля.

Для выяснения физического смысла этого условия поступим следующим образом. В системе отсчета, в которой заряд в данный момент покоится, вторая производная от скорости по времени равна, при пренебрежении силой торможения:

Во втором члене подставляем (ограничиваясь той же точностью)   и получаем:

Соответственно этому сила торможения будет состоять из двух членов:

 (75,10)

Если и есть частота движения, то   пропорицонально   и, следовательно, первый член порядка величины второй же — порядка 

Поэтому условие малости сил торможения по сравнению с действующей на заряд внешней силой   дает, во-первых:

или, вводя длину волны :  (75,11)

Таким образом, формула (75,8) для торможения излучением применима только в том случае, если длина падающей на заряд волны велика по сравнению с «радиусом» заряда  Мы видим, что расстояния порядка  опять оказываются той границей, за которой электродинамика приходит в противоречие сама с собой (см. § 37).

Во-вторых, сравнивая второй член в силе торможения с силой , находим условие  (75,12)

(или , где ). Таким образцом, необходимо также, чтобы само поле не было слишком велико. Поля  тоже являются границей, за которой классическая электродинамика приводит к внутренним противоречиям. И здесь надо иметь в виду, что в действительности электродинамика становится неприменимой, вследствие квантовых эффектов, уже при значительно меньших полях.

Напомним во избежание недоразумений, что длина волны в (75,11) и величина поля в (75,12) относятся к той системе отсчета, в которой частица в данный момент покоится.

22) Потенциалы Лиенара-Вихерта.

Потенциа́лы Лиена́ра — Ви́херта представляют собой простое лоренц-инвариантное выражение для потенциалов поля, создаваемого точечным электрическим зарядом, движущимся по заданной траектории.

23) Излучение быстродвижущегося заряда

( https://scask.ru/c_book_t_phis2.php?id=76 ).

Рассмотрим теперь заряженную частицу, движущуюся со скоростью не малой по сравнению со скоростью ввета.

Формулы § 67, выведенные в предположении и , неприменимы к этому случаю непосредственно. Мы можем, однако, рассматривать частицу в той системе отсчета, в которой она в данный момент покоится; в этой системе отсчета упомянутые формулы, очевидно, применимы (обращаем внимание на то, что это возможно сделать лишь в случае одной движущейся частицы; для нескольких частиц не существует, вообще говоря, системы отсчета, в которой бы все они одновременно покоились).

Таким образом, в указанной системе отсчета частица излучает в течение времени энергию

(согласно формуле (67,9)), где w — ускорение частицы в этой же системе. Полный же излучаемый ею импульс в рассматриваемой системе отсчета равен нулю

Действительно, излучение импульса определяется как интеграл от плотности потока импульса в поле излучения по замкнутой поверхности, охватывающей частицу. Но в силу свойств симметрии дипольного излучения импульсы, уносимые в противоположных направлениях, одинаковы по величине и противоположны по направлению; поэтому указанный интеграл обращается тождественно в нуль.

Для перехода к произвольной системе отсчета перепишем формулы (73,1) и (73,2) в четырехмерном виде. Легко видеть, что «излучение 4-импульса»  должно быть записано ка

Действительно, в системе отсчета, в которой частица покоится, пространственные компоненты 4-скорости и равны нулю, а  поэтому пространственные компоненты  обращаются в нуль, а временная дает равенство (73,1).

Полное излучение 4-импульса за время пролета частицы через данное электромагнитное поле равно интегралу от выражения (73,3), т. е.

Перепишем эту формулу в другом виде, выразив 4-ускорение   через тензор внешнего электромагнитного поля с помощью уравнений движения (23,4):

Мы получим тогда  (73,5)

Временная компонента уравнения (73,4) или (73,5) дает полное излучение энергии . Подставляя для четырехмерных величин их выражения через трехмерные величины, получим: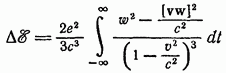

( — ускорение частицы), или, через внешние электрическое и магнитное поля: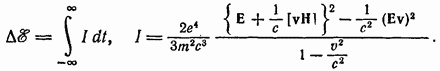

Выражения для полного излучения импульса отличаются лишним множителем v под знаком интеграла.

Из формулы (73,7) видно, что при скоростях, близких к скорости света, полное излучение энергии в единицу времени зависит от скорости в основном как   т. е. пропорционально квадрату энергии движущейся частицы. Исключение представляет только движение в электрическом поле параллельно направлению поля. В этом случае множитель  ), стоящий в знаменателе, сокращается с таким же множителем в числителе, и излучение оказывается не зависящим от энергии частицы.

24) Рассеяние электромагнитных волн свободными зарядами. Формула Томсона.

https://scask.ru/c_book_t_phis2.php?id=81

параграф 40

Если на систему зарядов падает электромагнитная волна, то под ее влиянием заряды приходят в движение. Это движение в свою очередь сопровождается излучением во все стороны; происходит рассеяние первоначальной волны.

Рассеяние удобно характеризовать отношением количества энергии, испускаемой рассеивающей системой в данном направлении в единицу времени к плотности потока энергии падающего на систему излучения. Это отношение имеет размерность площади и называется аффективным сечением (или просто сечением) рассеяния.

Пусть   есть энергия, излучаемая системой в телесный угол   (в 1 с) при падении на нее волны с вектором Пойнтинга S. Тогда сечение рассеяния (в телесный угол  ) равно

(черта над буквой означает усреднение по времени). Интеграл от   по всем направлениям есть полное сечение рассеяния.

Рассмотрим рассеяние, производимое одним неподвижным свободным зарядом. Пусть на этот заряд падает плоская монохроматическая линейно поляризованная волна. Ее электрическое поле можно написать в виде

Будем предполагать, что скорость, приобретаемая зарядом под действием поля падающей волны, мала по сравнению со скоростью света, что практически всегда выполняется.

Тогда можно считать, что сила, действующая на заряд, равна  , а силой   со стороны магнитного поля можно пренебречь.

В этом случае можно также пренебречь влиянием смещения заряда при его колебаниях под влиянием поля. Если заряд совершает колебания около начала координат, то можно тогда считать, что на него все время действует то поле, которое имеется в начале координат, т. е.

Поскольку уравнения движения заряда гласят

а его дипольный момент  , то

Для вычисления рассеянного излучения воспользуемся формулой (67,7) для дипольного излучения; мы имеем право сделать это, поскольку приобретаемая зарядом скорость предполагается малой. Заметим также, что частота излучаемой зарядом (т. е. рассеянной им) волны равна, очевидно, частоте падающей волны.

Подставляя (78,2) в (67,7), находим:

где n — единичный вектор в направлении рассеяния. С другой стороны, вектор Пойнтинга падающей волны равен

Отсюда находим сечение рассеяния в телесный угол  :

где   — угол между направлением рассеяния и направлением электрического поля Е падающей волны. Мы видим, что сечение рассеяния свободным зарядом не зависит от частоты.

Определим полное сечение а. Для этого выберем направление Е в качестве полярной оси; тогда   и, интегрируя по   от   до   и по   от   до  , находим: (так называемая формула Томсона).

25) Рассеяние электромагнитных волн осциллятором. Учет силы трения излучением.

Рассеяние:

26) Понятия микро- и макрополя в среде. Усреднение. Электрическая напряженность и магнитная индукция в среде. (2.1)

27) Свободные и связанные заряды. Вектор поляризации. Объемные и поверхностные связанные заряды. Вектор электрической индукции.

Свободные заряды – это заряды, перемещающиеся под действием поля на существенные расстояния. Например, электроны в проводниках, ионы в газах и заряды, привносимые извне на поверхность диэлектриков, которые нарушают их (диэлектриков) нейтральность. Заряды, входящие в состав нейтральных, в целом, молекул диэлектриков, так же, как ионы, закрепленные в кристаллических решетках твердых диэлектриков около положений равновесия, получили название связанных зарядов. Вектор поляризации — векторная физическая величина, равная дипольному моменту единицы объёма вещества, возникающему при его поляризации, количественная характеристика диэлектрической поляризации^[1].

Обозначается буквой   , в Международной системе единиц (СИ) измеряется в Кл/м².

Диэлектрическая поляризация обусловлена смещением связанных зарядов вещества во внешнем электрическом поле относительно их расположения при отсутствии внешнего электрического поля. Если выделить какой-либо объём в диэлектрике, то в результате приложения поля на его поверхности могут возникнуть поверхностные электрические заряды   . Такие заряды могут возникнуть или благодаря смещению электронной оболочки относительно ядра атома, или же в результате переориентации молекул, которые имеют собственный дипольный момент.

Нормальную к поверхности составляющую вектора поляризации определяют как