1 4. Кинетическая энергия материальной точки.

- по 2 закону ньютона

  - кинетическая энергия материальной точки массой  , движущейся со скоростью  . Изменение кинетической энергии материальной точки на некотором перемещении равно работе, совершаемой силой, под действием которой точка движется:

15. Полная механическая энергия материальной точки. Консервативные, неконсервативные силы.

Связь работы и кинетической энергии A₁₂ = W_k2 - W_k1, Связь работы и потенциальной энергии A₁₂ = W_n1 - W_n2. Отсюда W_n1 - W_n2 = W_k2 - W_k1 или W_k1 + Wn1 = W_k2 + W_n2.

Пусть некоторая частица находится в стационарном поле консервативных сил.

Со стороны этого поля на частицу действует консервативная сила F_конс. Работа, совершаемая этой силой, с одной стороны, идёт на приращение кинетической энергии частицы, движущейся под действием силы F_конс, а с другой – равна убыли потенциальной энергии этой частицы. Но это значит, что приращение кинетической энергии частицы равно убили её потенциальной энергии. Перегруппировав члены этого уравнения, получаем. Из этого следует, что сумма кинетической и потенциальной энергии частицы, движущейся в стационарном консервативном поле, остаётся постоянной. Величину называют полной механической энергией частицы.

16. Система частиц. Внутренние и внешние силы. Потенциальная энергия системы. Собственная энергия.

Внешние силы - это такие силы, которые действуют только на поверхность предмета, но не проникают внутрь его. К этим силам относятся все силы, развиваемые материальным объектом. Внутренние силы - это такие силы, которые действуют сразу на все атомы передвигаемого предмета независимо от того, где они находятся: на поверхности или в середине предмета. К этим силам относятся силы инерции и силы поля: гравитационного, электрического, магнитного. В механике внешними силами по отношению к данной системе материальных точек (т. е. такой совокупности материальных точек, в которой движение каждой точки зависит от положений или движений всех остальных точек) называются те силы, к-рые представляют собою действие на эту систему других тел (других систем материальных точек), не включенных нами в состав данной системы.

Потенциальная энергия — механиче­ская энергия системы тел, определяемая их взаимным расположением и характе­ром сил взаимодействия между ними. Пусть взаимодействие тел осуществля­ется посредством силовых полей (напри­мер, поля упругих сил, поля гравитацион­ных сил), характеризующихся тем, что работа, совершаемая действующими сила­ми при перемещении тела из одного поло­жения в другое, не зависит от того, по какой траектории это перемещение прои­зошло, а зависит только от начального и конечного положений. Такие поля на­зываются потенциальными, а силы, дей­ствующие в них, — консервативными. Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипативной; ее примером является си­ла трения.

17. Полная энергия системы материальных точек. Закон сохранения энергии.

Умножим скалярно на  ,и просуммируем результат по всем точкам системы: Слева стоит дифференциал кинетической энергии системы точек Кинетическую энергию используя систему отсчета с началом в центре масс (будем называть ее ЦСО), удобно представить в виде

Таким образом мы показали, что кинетическая энергия системы материальных точек равна сумме кинетической энергии системы частиц в их движении относительно ЦСО и кинетической энергии «центра масс» т. е. кинетической энергии системы в предположении, что вся масса системы точек сосредоточена в центре масс (теорема Кенига).

Предположим, что внешние и внутренние силы потенциальны и консервативны². Тогда выражение является полным дифференциалом скалярной функции  , имеющей смысл потенциальной энергии системы частиц во внешнем поле. Если, кроме того,  удовлетворяют третьему закону Ньютона, то они могут быть построены с помощью некоторой функции (15.5) как . (16.5)

Учитывая, что  и  ,где f —скалярная функция аргумента , преобразуем двойную сумму: .(17.5) Здесь мы использовали очевидное соотношение . Коэффициент 1/2 появился в (17.5), так как при суммировании по i, j каждый индекс данной пары появляется дважды: при суммировании по i и по j. Мы видим, что можно определить потенциальную энергию системы точек как и если внешние и внутренние силы консервативны, то, собирая все члены вместе, получим . (18.5) Эти равенства выражают собой закон сохранения полной механической энергии системы материальных точек. На их основе можно сформулировать теорему: Полная механическая энергия консервативной системы материальных точек не изменяется во время движения.

Билет 18. Задача двух тел. Приведенная масса

Рассмотрим задачу о движении двух взаимодействующих толь­ко между собой материальных точек. Вследствие однородности и изотропности пространства потенциальная энергия взаимодей­ствия может зависеть только от расстояния между точками. Функ­ция Лагранжа для данной задачи запишется в форме:

 

Рассматриваемая система материальных точек замкнута. Поэтому ее импульс сохраняется, и система отсчета центра инерции являет­ся инерциальной системой отсчета. Задачу будем решать в систе­ме отсчета центра инерции. Начало координат поместим в центр инерции, что дает

Введем радиус-вектор  , направленный от первой материальной точки ко второй:

С помощью формул выразим векторы   и    через вектор   :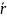

Потенциальная энергия теперь зависит только от величины век­тора    . Выражая с помощью формул (4.4) скорости   и   через вектор  , кинетическую энергию системы двух материальных точек можно записать как кинетическую энергию одной матери­альной точки массой

Выраженная через радиус-вектор функция Лагранжа запи­шется в форме  (4.6)

Функция Лагранжа (4.6) — это функция Лагранжа одной мате­риальной точки массы  , движущейся в потенциальном поле, за­висящем только от расстояния до начала координат. Такое потен­циальное поле называется Центральным полем. Сила, действую­щая в центральном поле на материальную точку, направлена по прямой, соединяющей материальную точку с центром поля:  (4.7)

Масса  , определенная согласно (4.5), называется Приведенной массой. Следовательно, решение задачи двух тел эквивалентно решению задачи о движении в центральном поле материальной точки с массой, равной приведенной массе. После решения задачи о движении материальной точки в центральном поле координаты двух тел можно получить при помощи формул (4.4).

Если масса одной материальной точки, например  , много больше массы другой материальной точки, то из формул (4.4) и (4.5) получим, что приближенно  ,  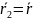,  , то есть центр инерции системы двух тел совпадает с более массивным те­лом, а приведенная масса равна массе менее массивного тела. В этом случае задача двух тел сводится к задаче о движении одного тела в потенциальном поле, создаваемом другим телом.

Поскольку масса Солнца намного больше массы каждой из пла­нет Солнечной системы, то в первом приближении можно прене­бречь взаимодействием планет между собой и движением Солнца вокруг центра инерции Солнечной системы. В этом приближении движение отдельной планеты рассматривается как движение ма­териальной точки в поле тяготения Солнца. Учет взаимодействия планет между собой приводит к задаче многих тел, взаимодейству­ющих между собой. Эта задача не может быть сведена к квадра­турам и решается приближенными методами.

Билет 19. Упругое, неупругое столкновение двух частиц. Отражение от стенки. Замедление нейтронов.

Абсолютно упругим ударом двух тел в нерелятивистском случае называется такое столкновение, после которого не остается никаких деформаций, не изменяется их внутренняя энергия (шары не нагреваются), а полная кинетическая энергия до удара равна полной кинетической энергии тел после удара. Рассмотрим центральный удар абсолютно упругих шаров. В этом случае скорости шаров до удара  и   направлены вдоль прямой, соединяющей их центры. Эта прямая называется линией центров. В случае абсолютно упругого удара шары при столкновении деформируются, и кинетическая энергия частично переходит в потенциальную энергию упругих деформаций. В некоторый момент вся кинетическая энергия относительного движения переходят в потенциальную энергию упруго деформированных шаров. В этот момент шары аналогичны сжатым пружинам, стремящимся перейти в недеформированное состояние. Ввиду этого начинается обратный переход энергии упругих деформаций в кинетическую энергию поступательного движения шаров. Когда он заканчивается, шары разлетаются в разные стороны и вновь оказываются недеформированными. Таким образом, кинетическая энергия поступательного движения шаров снова принимает исходное значение, каким оно было до удара. Скорости шаров после столкновения   и    легко найти из законов сохранения импульса и потенциальной энергии 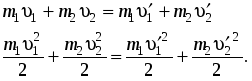  (7.18)  Такая система должна иметь решение относительно неизвестных   и   . Одно решение очевидно  ,   . Но это решение означает, что столкновения не было. Это связано с тем, что в законах столкновения мы рассматриваем два состояния, разделенных промежутком времени  , но в законе сохранения не заложено условие, что это столкновение произошло. Чтобы получить решение, относящееся к столкновению, нужно потребовать. чтобы скорости изменилась. Заметив это, перепишем (7.18) в виде Поделив уравнения почленно друг на друга, получим В результате задача сводится к решению системы двух линейных уравнений Решение этой системы уравнений имеет следующий вид Рассмотрим несколько частных случаев столкновения двух шаров. 1. Пусть два шара перед столкновением имеют импульсы, равные по величине, но противоположные по направлению, то есть  . Тогда, согласно полученным формулам, скорости шаров после удара равны соответственно   и   и, следовательно, в результате столкновения импульсы шаров изменяются на противоположные по направлению и шары разлетаются с прежними по величине скоростями. 2. Пусть один из шаров покоится,  . Скорости шаров после столкновения  ,  .  Таким образом, после столкновения оба шара будут иметь скорости, отличные от нуля, но их величины   и   будут зависеть от соотношения масс шаров, участвующих в столкновении. а) при   скорость первого шара уменьшается по величине, но сохраняет свое направление. Часть кинетической энергии этого шара передается второму шару. Кинетическая энергия, приобретенная вторым шаром  .  Очевидно, переданная второму шару энергия максимальна, когда  . В этом случае первый шар останавливается, а вся его энергия   переходит в кинетическую энергию второго шара  . Если  , то переданная энергия   мала. Импульс второго шара после удара 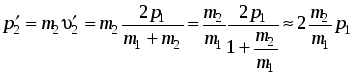  также мал по сравнению с  , хотя скорость   мало отличается от  Действительно,  . b) При   направление движения первого шара изменяется на противоположное  , а второй шар начнет двигаться в направлении движения первого шара до столкновения  . При   от первого шара второму переходит энергия  , то есть малая ее часть. Импульс второго шара  , а скорость .  Например, при ударе шара о стенку можно принять  , тогда  , а  , и, следовательно, шар отскакивает от стенки, сохраняя кинетическую энергию неизменной. Можно решить задачу о столкновении в системе центра масс (Ц - системе). Относительно лабораторной системы отсчета центр масс движется со скоростью . Если воспользоваться теперь нерелятивистским законом сложения скоростей, то для скоростей частиц после столкновения получим следующие выражения ,  . Таким образом в системе центра масс столкновение приводит просто к изменению знака каждой скорости.

Замедление нейтронов Особенности упругого удара имеют многие важные применения, например, для замедления нейтронов в ядерном реакторе. Энергия, которая выделяется в ядерных реакторах — это энергия деления ядер урана при столкновении их с нейтронами. Вероятность захвата нейтрона тем больше, чем меньше их кинетическая энергия. Для ее уменьшения в активную зону реактора вводится графит, масса ядра атома углерода, который входит в графит, приблизительно в 12 раз больше массы нейтрона. Поэтому при каждом центральном столкновении нейтрона с ядром графита ядру передается   энергии нейтрона и процесс замедления идет быстро.

Абсолютно неупругий удар Интересным примером, где имеет место переход механической энергии в другие виды энергии под действием диссипативных сил, является абсолютно неупругий удар. Так называется столкновение двух тел, в результате которого они соединяются вместе и движутся дальше как одно тело.  Н айти скорость тела можно не вдаваясь в механизм явления, а используя только закон сохранения импульса. Рассмотрим центральный удар. Пусть два шара массами  и   движутся со скоростями  и  . При столкновении образуется тело массой   , движущееся со скоростью . Запишем закон сохранения импульса для такого удара  . В проекции на ось, совпадающую по направлению со скоростью движущихся частиц, закон сохранения импульса запишется следующим образом

О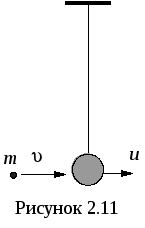 тсюда скорость движения слипшегося тела после столкновения Изменение механической энергии системы для рассматриваемого случая равно изменению ее кинетической энергии где  - приведенная масса системы.  Таким образом, при столкновении двух абсолютно неупругих шаров происходит потеря кинетической энергии макроскопического движения, равная половине произведения приведенной массы на квадрат относительной скорости. Во время столкновения в системе действуют диссипативные силы, уменьшающие кинетическую энергию макроскопического движения. Поэтому применять закон сохранения механической энергии к процессам, происходящим во время удара, нельзя. Но после того, как удар закончился и тела соединились, законом сохранения механической энергии уже можно пользоваться. В качестве примера можно рассмотреть задачу о баллистическом маятнике. Пусть на маятник массой  налетает со скоростью  пуля массой  . Для простоты расчета будем считать маятник математическим. Процесс столкновения происходит настолько быстро, что за время столкновения, маятник не успевает отклониться на заметный угол. В результате удара он только приходит в движение и задача заключается в том, чтобы найти скорость после удара. Во время удара всеми силами, действующими на маятник, можно пренебречь по сравнению с силой, с которой на маятник действует налетающая пуля, то есть систему маятник-пуля можно считать замкнутой и использовать закон сохранения импульса. В проекции на направление движения пули закон сохранения импульса выглядит следующим образом , где   - скорость системы после удара. После удара диссипативные силы не действуют, поэтому можно использовать закон сохранения механической энергии где 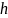 - высота, на которую поднимется маятник, . Измерив  , можно вычислить скорость пули .