
573
.pdf
Уравнение (11.1) мы получили по второму закону Ньютона, который является основным законом динамики и гласит, что производная по времени от количества движения материальной точки равна действующей на неѐ силе, т. е.
(mv) = F |
(11.2) |
где v – скорость точки M.
Считая массу постоянной, можно представить уравне-
ние (11.2) в виде |
|
или |
. |
Итак, уравнение (11.1) в проекции на ось τ даст нам одно из естественных уравнений движения точки по заданной
неподвижной гладкой кривой: |
|
|
|||||||||
|
|
|
|
|
|
или |
|
= . |
|||
|
|
|
|
||||||||
В нашем случае получим в проекции на ось τ |
|||||||||||
|
|
|
|
|
|
|
|
|
, |
||
где m – масса маятника. |
|||||||||||
|
|
||||||||||
Так как v = l |
или v = l |
|
, отсюда находим |
||||||||
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Сокращая на m и полагая
, |
(11.3) |
будем окончательно иметь:
. (11.4)
Рассмотрим сначала случай малых колебаний. Пусть в начальный момент маятник отклонѐн от вертикали на угол φ0 и опущен без начальной скорости. Тогда начальные условия будут:
221

при = 0, |
, ̇ |
. |
(11.5) |
||
Из интеграла энергии: |
|
|
|
||
|
|
|
|
, |
(11.6) |
|
|
|
|
||
где V потенциальная энергия, а h — постоянная интегрирования, следует, что при этих условиях в любой момент времени угол φ ≤ φ0. Значение постоянной h определяется по начальным данным. Допустим, что угол φ0 мал; тогда угол φ будет также мал и можно приближѐнно положить sin φ ≈ φ. При этом уравнение (11.4) примет вид
. (11.7)
Уравнение (11.7) есть дифференциальное уравнение простого гармонического колебания. Общее решение этого уравнения имеет вид
, (11.8)
где A и B или a и ε суть постоянные интегрирования.
Отсюда сразу находим период T малых колебаний математического маятника (период промежуток времени, в течение которого точка возвращается в прежнее положение с той же скоростью)
и
,
т.к. sin имеет период равный 2 , то ωT=2 , следовательно
T = |
|
√ |
|
(11.9) |
|
|
Для нахождения закона движения при начальных условиях (11.5) вычисляем:
̇ |
(11.10) |
Подставляя значения (11.5) в уравнения (11.8) и (11.10), получим:
222

φ0 = A, 0 = ωB,
т.е. B=0. Следовательно, закон движения для малых колебаний будет:
φ = φ0 cosωt. |
(11.11) |
Найдѐм теперь точное решение задачи о плоском мате- |
|
матическом маятнике. Определим сначала первый интеграл уравнения движения (11.4). Так как
|
|
|
|
|
|
̇ |
̇ |
|
̇ |
̇ |
||||
|
|
|
= |
|
|
|
|
|
|
|
, |
|||
|
|
|
|
|
|
|
|
|
||||||
то (11.4) можно представить в виде |
|
|
|
|
||||||||||
|
|
|
|
|
̇ ̇ |
|
|
. |
|
|
||||
Отсюда, умножая обе части уравнение на dφ и интегри- |
||||||||||||||
руя, получим: |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
̇ |
|
|
|
|
|
|
. |
|
(11.12) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Обозначим здесь через φ0 угол максимального отклоне- |
||||||||||||||
ния маятника; тогда при φ = φ0 |
будем иметь ̇ , откуда |
|||||||||||||
C = ω2 cos φ0. В результате интеграл (11.12) даѐт: |
||||||||||||||
|
̇ |
|
|
|
|
|
|
, |
(11.13) |
|||||
где ω определяется равенством (11.3).
Этот интеграл представляет собой интеграл энергии и
может быть непосредственно получен из уравнения |
|
|||||
|
|
|
|
|
, |
(11.14) |
|
|
|
||||
где |
работа на перемещении M0M активной силы |
|||||
F, если учесть, |
что в нашем случае v0=0, |
̇и |
||||
Из уравнения (11.13) видно, что при движении маятника угол φ будет изменяться между значениями +φ0 и φ0 (|φ|<φ0, так как ̇ ), т.е. маятник будет совершать колебательное движение. Условимся отсчитывать время t от момента про-
223

хождения маятника через вертикаль OA при его движении право (см. рисунок 1). Тогда будем иметь начальное условие:
при t = 0,φ = 0. |
(11.15) |
Кроме того, при движении из точки A будет ̇ |
; из- |
влекая из обеих частей равенства (11.13) квадратный корень, получим:
√ .
Разделяя здесь переменные, будем иметь:
. (11.16)
√
Так как
,
,
то
.
Подставляя этот результат в уравнение (11.16), получаем:
. (11.17)
√
Чтобы проинтегрировать уравнение (11.17), нужно найти квадратуру левой части. Для этого перейдѐм от переменной φ к новой переменнойα, полагая:
, |
(11.18) |
где . Тогда
,
откуда
.
√
224

Кроме того, |
|
|
|
. |
|
|
Подставляя все эти величины в уравнение (11.17) и заменяя ω его значением (11.3), получим:
|
|
√ |
|
. |
(11.19) |
|
|
|
|
||||
√ |
||||||
|
|
|
|
|||
По принятым начальным условиям (11.15) при t=0 угол φ=0, а, следовательно, как видно из (11.18), и α=0. Тогда, беря от обеих частей уравнения (11.19) определѐнные интегралы справа от 0 до t, а слева от 0 до α, получим закон движения маятника в виде
∫ |
|
|
√ |
|
. |
(11.20) |
√ |
|
|
||||
|
Интеграл, стоящий в левой части равенства (11.20),
представляет собой эллиптический интеграл первого рода.
Величина k называется модулем эллиптического интеграла. Этот интеграл есть функция верхнего предела и модуля, т.е.
∫ |
|
|
. |
(11.21) |
√ |
|
|||
|
Если в равенстве (11.21) рассматривать верхний предел a как функцию от интеграла u, то такая функция носит название амплитуды u и обозначается так:
, или |
. |
(11.22) |
Беря от обеих частей равенства (11.22) синус, мы полу-
чим:
. (11.23)
Функция snu (синус-амплитуда u) представляет собой так называемую эллиптическую функцию Якоби. Поскольку,
согласно уравнению (11.20), u=√ , то, переходя в равенстве
225

(11.23) от α к φ с помощью формулы (11.18), найдѐм закон движения маятника, выраженный эллиптическую функцию sn, в виде
√ . (11.24)
11.1.4. Период колебаний математического маятника в общем случае
Найдѐм период T колебания маятника. Из положения φ = 0 в положение φ = φ0 маятник приходит за четверть периода. Так как, согласно равенству (11.18), при φ = 0 и = 0, а при φ = φ0 величина , то из уравнения (11.20) имеем:
√ |
|
|
|
∫ |
|
|
|
. |
(11.25) |
|
|
√ |
|
|
|||||
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
Таким образом, определение периода колебаний маятника сводится к вычислению величины
∫ |
|
|
( |
|
) |
, |
(11.26) |
|
|
|
|
||||||
√ |
||||||||
|
|
|
|
|
|
|||
представляющий собой четверть периода эллиптического интеграла (11.21).
Известно (формула Валлиса), что
∫ |
|
|
|
. |
(11.27) |
|
|
Разлагая в выражении (11.26) подынтегральную функцию в ряд, получим:
.
√
Тогда, используя формулу (11.27), будем иметь:
∫ |
|
|
|
|
[ |
( |
|
) |
|
] (11.28) |
|
|
|
|
|
|
|||||||
√ |
|||||||||||
|
|
|
|
|
|
|
|
|
|||
Подставляя это значение K в равенство (11.25) и учитывая, что
226

, получим для периода колебаний плоского матема-
тического маятника выражение
T=2 √ |
|
[ |
( |
|
) |
|
|
|
|
|
]. (11.29) |
|
|
|
|
|
Следовательно, чем больше φ0 (угол размаха), тем больше период колебания маятника. Таким образом, математический маятник свойством изохронности не обладает. Если при малых размерах ограничиться в формуле (11.29) только двумя первыми членами, то, полагая , получим приближѐнное выражение периода
T 2 √ |
|
|
|
. |
(11.30) |
|
|
Таким образом, получено уравнение простого гармонического колебания, закон движения для малых колебаний, закон движения маятника через эллиптическую функцию, а также выражение для периода колебаний маятника.
11.2. Задача о двойном математическом маятнике
В лагранжевой механике для описания системы исполь-
зуются обобщенные координаты и обобщенные скорости. В
нашем случае в качестве таких переменных можно взять уг-
лы отклонения маятников α |
, α |
2 |
и их угловые скорости |
̇, |
̇. |
1 |
|
|
1 |
2 |
Используя указанные переменные, построим лагранжиан двойного маятника и запишем дифференциальные уравнения Лагранжа. Упрощенная модель двойного маятника показана на рисунке 2. Будем считать стержни невесомыми. Их длины равны l1 и l2. Массы точечных тел (они представлены шарами конечного радиуса) составляют m1 и m2. В точках подвеса (шарнирах) трение отсутствует.
227
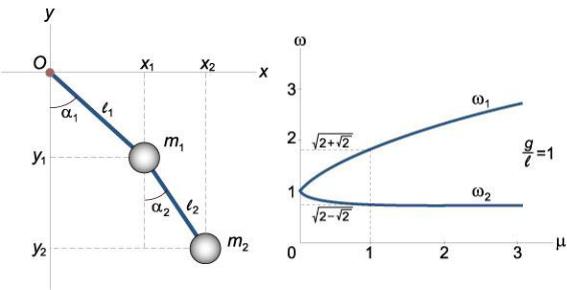
Рис. 2. Упрощенная модель |
Рис. 3. Зависимость частот ω1, |
двойного маятника |
ω2 от параметра μ |
Введем систему координат Oxy, начало которой совпадает с точкой подвеса O. Координаты маятников определяются следующими соотношениями:
|
, |
|
|
|
|
. |
|||
Кинетическая и потенциальная энергия маятников (со- |
|||||||||
ответственно T и V) выражаются формулами |
|
|
|||||||
T = |
|
|
|
|
( ̇ ̇) |
( ̇ ̇) |
|||
|
|
|
|
|
|
|
|
|
|
Тогда лагранжиан записывается в виде |
|
|
|
||||||
L = T-V = T +T |
-(V |
+V |
) = |
|
( ̇ ̇) |
|
( ̇ ̇) |
||
|
|
||||||||
1 |
2 |
1 |
2 |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
С учетом того, что |
|
|
|
|
|
|
|||
̇= l1 |
|
̇, |
̇ l1 |
̇+ l2 |
|
|
̇, |
||
̇ |
|
̇, |
̇= |
̇ |
̇ |
̇. |
|||
Следовательно,
228

Т = |
|
( ̇ ̇) |
|
( |
|
|
̇ |
|
|
̇ |
|
|
) |
|
|
̇ |
||||||||
|
|
|
|
|
||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т = |
|
|
( ̇ ̇) |
|
|
|
̇ |
|
|
|
|
|
̇ |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
̇ |
|
̇ |
|
|
|
* |
|
|
̇ |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
̇ |
|
̇ ̇ |
|
|
|
|
|
|
̇ |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
̇ |
̇ ̇ |
|
+ |
|
|
|
* |
̇ |
|
|
̇ |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
̇ ̇ |
+ |
|
|
|
|
|
||||||
|
|
V1 = m1 g y1 = m1 g l1 |
, |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
V2 = m2 g y2 = m2 g (l1 |
|
+l2 |
). |
|
|
|
|
|
||||||||||||||
|
|
В результате лагранжиан системы принимает такой вид: |
||||||||||||||||||||||
|
|
|
|
|
|
|
L = T V = T1+T2 |
(V1+V2) = |
|
|
|
|
||||||||||||
|
|
|
|
|
|
̇ |
̇ |
|
̇ ̇ |
|
|
|
|
|
|
|||||||||
|
= |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
g |
|
|
|
+ |
g |
, |
|
|
|
|
|||||
где |
|
|
m1 +m2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Для данной задачи уравнения Лагранжа запишем в виде: |
||||||||||||||||||||||
̇
Входящие в эти уравнения частные производные выражаются следующими формулами:
|
|
̇ |
̇ |
|
̇ |
||||
|
|
|||
|
|
|
̇ ̇ |
|
|
|
|
||
|
|
̇ |
̇ |
|
̇ |
||||
|
|
|||
̇ ̇
Следовательно, первое уравнение Лагранжа записывается как
229

|
|
|
̇ |
̇ |
|
|
|
||
|
|
|
̇ ̇ |
|
|
̈ |
̈ |
̇ |
|
|
|
̇ |
̇ + |
̇ ̇ |
|
̈ |
̈ |
̇ ̇ |
̇ |
|
|
||
|
̇ ̇ |
|
̈ |
̈ |
̇ |
|
||
Сокращая на l1 ≠ 0, получаем: |
|
||
̈ |
̈ |
+ |
̇ |
|
|||
|
+ g |
|
. |
Аналогично выведем второе дифференциальное уравне-
ние:
̇̇
̇̇
|
̈ |
̈ |
|
̇ |
̇ ̇ |
|
̇ ̇ |
|
|
̈ |
̈ |
|
̇ |
̇ ̇ |
|
|
230 |
