
Автоколебания, метод многих масштабов
.pdfАвтоколебания, метод многих масштабов
Дано следующее безразмерное уравнение с начальными условиями:
x¨ + x ϵ |
x˙ |
x˙3 |
= 0, |
|
||
|
|
|
||||
− 6 |
(1) |
|||||
x(0) =−0, |
|
|ϵ| 1. |
||||
x˙(0) = v0;
Требуется найти ассимптотическое разложение решения уравнения методом многих масштабов с точностью до порядка ϵ, а также решить его численно при v0 = 1, ϵ = ±0.05, используя симплектический метод; решения сравнить, построив фазовые траектории.
Согласно используемому методу вводятся так называемые быстрое время и медленное время, t и t1 соответственно:
t = t; t1 = ϵt.
Тогда решение уравнения ищется в следующем виде:
x = x(t, t1) = x0(t, t1) + ϵx1(t, t1) + O(ϵ2).
Перепишем выражения для операторов дифференциирования:
|
|
|
d |
= |
∂ |
+ ϵ |
∂ |
|
; |
||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
dt |
|
∂t |
|
∂t1 |
||||||
d2 |
= |
|
∂2 |
+ 2ϵ |
∂2 |
|
|
+ O(ϵ2). |
|||||
dt2 |
∂t2 |
∂t∂t1 |
|||||||||||
|
|
|
|
|
|
||||||||
С учетом полученных выражений уравнение из системы (1) перепишется в виде
|
|
∂2 |
∂2 |
+ O(ϵ2) |
x0 + ϵx1 + O(ϵ2) + |
x0 + ϵx1 + O(ϵ2) − |
|
|
||||||||||||||||||||
|
|
|
+ 2ϵ |
|
|
|
|
|
||||||||||||||||||||
−ϵ |
∂t2 |
∂t∂t1 |
3 |
! = 0. |
||||||||||||||||||||||||
∂t |
+ ϵ∂t1 |
x0 + ϵx1 + O(ϵ2) − 6 |
∂t + ϵ |
∂t1 x0 + ϵx1 + O(ϵ2) |
|
|||||||||||||||||||||||
|
|
∂ |
|
|
|
∂ |
|
|
|
|
|
|
1 |
|
∂ |
∂ |
|
|
|
|
|
|
|
|||||
Отбрасывая здесь слагаемые порядка выше ϵ, получим |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
∂2x |
∂2x |
|
|
∂2x |
|
|
|
|
∂x |
|
ϵ ∂x |
3 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
0 |
+ ϵ |
1 |
+ 2ϵ |
0 |
+ x0 |
+ ϵx1 − ϵ |
|
0 |
|
+ |
|
|
0 |
= 0. |
|
|
|||||||
|
|
|
|
|
∂t2 |
∂t2 |
∂t∂t1 |
|
∂t |
6 |
∂t |
|
|
|||||||||||||||
1

Собрав слагаемые относительно порядков ϵ, получим уравнения
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϵ |
0 |
: |
|
∂2x0 |
|
|
+ x0 |
= 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂2x |
|
|
|
|
|
|
∂x |
|
|
|
|
1 |
|
|
|
|
|
∂x |
|
3 |
|
|
|
|
∂2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ϵ1 : |
|
1 |
+ x1 = |
|
|
0 |
− |
|
|
|
0 |
|
|
|
− 2 |
0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∂t2 |
|
|
∂t |
6 |
∂t |
|
|
∂t∂t1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
Первое уравнение из (2) имеет решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 = A(t1)eit + |
|
|
(t1)e−it. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= iAeit − iAe−it; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂2x0 |
|
|
|
|
|
|
|
|
|
|
|
it |
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
it |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= iA′e |
|
|
− iA |
e− |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t∂t1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Подставим полученные выражения во второе уравнение из (2): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
∂2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iA′eit − iA′e−it ; |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
1 |
+ x1 = iAeit − iAe−it − |
|
iAeit − iAe−it |
|
− 2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
∂t2 |
6 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
∂2x1 |
|
|
|
|
|
|
|
|
|
|
|
iA3 |
|
|
|
|
iA2 |
|
|
it |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
it |
|
|
|
−it |
|
3it |
|
|
|
A |
|
|
|
|
|
|
iAA |
|
|
−it |
|
|
|
|
iA |
−3it |
|
|
|
′ |
it |
|
|
|
|
|
|
′ |
−it |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
+ x1 = iAe |
|
− iAe |
|
|
|
+ |
|
e |
|
|
− |
|
|
|
|
e |
|
|
+ |
|
|
|
|
|
|
|
|
e |
|
|
|
− |
|
|
e |
|
− 2iA e |
|
+ 2iA e |
|
; |
|||||||||||||||||||||||||||||||||||||||
∂t2 |
|
|
|
|
6 |
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
6 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2x |
|
|
|
|
|
iA2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iA3 |
|
|
|
|
3 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iAA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iA |
|
|
||||||||||||||||||||||||||||
|
∂ 1 |
+ x1 = iA − |
|
|
|
− 2iA′ eit + −iA + |
|
|
|
|
|
|
|
+ 2iA′!e−it + |
|
|
e3it |
− |
|
|
e−3it. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
∂t2 |
2 |
|
|
2 |
|
|
|
|
|
6 |
|
6 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Во избежание резонанса амплитуды при гармониках, совпадающих с собственной частотой
колебаний, должны равняться нулю: |
|
|
|
|
|
|
|
|
|
|
|
|
( |
A + AA |
|
+ 2A′ = 0. |
(3) |
||||||||
A |
− A22 |
A |
|
|
−2 2A |
′ = 0, |
|
|||||
|
|
|
|
|
|
|||||||
− |
|
|
|
|
|
|
|
|
||||
2 |
|
|
|
|
|
|
||||||
Уравнения системы (3) являются сопряженными, поэтому рассмотрим ттолько одно из
них: |
|
|
|
dA |
|
|
2A − A|A|2 |
|
|
|
||||||
|
|
|
|
|
= |
. |
|
|
||||||||
|
|
|
|
dt1 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||
Представим комплексное число A в показательной форме: |
||||||||||||||||
|
|
|
A = R(t1)eiϕ(t1) = |
|
||||||||||||
|
dR |
eiϕ + i |
dϕ |
Reiϕ = |
2Reiϕ − R3eiϕ |
= |
||||||||||
|
dt1 |
|
|
|
|
|
||||||||||
|
|
|
dt1 |
|
|
|
|
4 |
|
|
|
|||||
|
|
|
dR |
+ i |
dϕ |
R = |
2R − R3 |
. |
|
|||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
dt1 |
|
dt1 |
4 |
|
|
|
|||||||
Сравнивая вещественные и мнимые части чисел, стоящих в правой и левой частях уравнения, получим
2
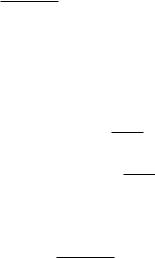
(dt1 |
= |
−4 ; |
|
|
dϕ |
= 0, |
|
|
|
dt1 |
|
2R R3 |
|
= ϕ(t1) = ϕ0. |
dR |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
2R − R3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
dR |
= |
|
|
|
= R(t |
) = |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
dt1 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
√C0e−t1 + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
x0 = Aeit + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
Ae−it |
= x0(0, 0) = 0 = A(0) + A(0); |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t0 |
t,t1=0 = v0 = iA(0) − iA(0) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iv0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A(0) = |
− |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
A(0) = R |
eiϕ0 = |
|
|
|
|
R |
(cos ϕ |
|
+ i sin ϕ |
) = |
|
−iv0 |
|
= |
|
|
|
cos ϕ |
|
|
|
|
= 0 = |
ϕ |
|
= |
− |
π |
; |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R0 |
|
= |
|
v0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
R(0) = R0 = |
|
v0 |
= |
|
√ |
|
2 |
|
|
|
|
= C0 = |
|
8 |
|
|
|
− 1 = |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
v02 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
C0 + 1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
v0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R(t1) = |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p(8 − |
|
v2 |
|
e |
|
t1 + v2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0) |
− |
|
√ |
|
v00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
A = R(t1)eiϕ(t1) = −i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
t1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
Возвращаясь к уравнению для x1, получим p(8 − v0)e− |
|
|
|
|
+ v0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
∂2x1 |
+ x1 |
= − |
|
|
|
|
|
|
|
|
|
|
23/2v03 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
3it |
+ e |
−3it |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
∂t2 |
|
6 ((8 − v02)e−t1 + v02)3/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
∂2x1 |
|
|
|
|
= − |
|
|
|
|
|
|
|
|
23/2v03 cos 3t |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
+ x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
∂t2 |
3 ((8 − v02)e−t1 + v02)3/2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
x1 = |
|
− |
|
|
|
|
|
|
|
|
|
|
|
23/2v03 |
|
|
|
|
|
|
|
|
|
|
|
Z0 |
t |
sin (t |
− |
|
τ) cos 3τ dτ; |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
3 ((8 − v02)e−t1 + v02)3/2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x1 = − |
|
|
|
|
|
|
|
|
|
23/2v03 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
t cos t. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
6 ((8 − v02)e−t1 + v02)3/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Таким образом, запишем общее решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
√ |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2v0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2ϵv0 |
|
|
|
|
2 |
|
|
|
2 |
|
|||||||||||||||||||
x(t, t1) = x0(t, t1)+ϵx1(t, t1) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
t cos t+O(ϵ |
). |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
С учетом t1 = ϵt получим p(8 − v02)e−t1 + v02 |
|
|
|
|
|
|
|
− |
6 ((8 − v02)e−t1 + v02)3/2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2√ |
|
v0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2√ |
|
ϵv03 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||||||
x(t) = |
|
|
sin t |
|
|
|
|
sin |
t cos t + O(ϵ |
). |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
p |
|
|
6 ((8 − v02)e−ϵt + v02)3/2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(8 − v02)e−ϵt + v02 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3
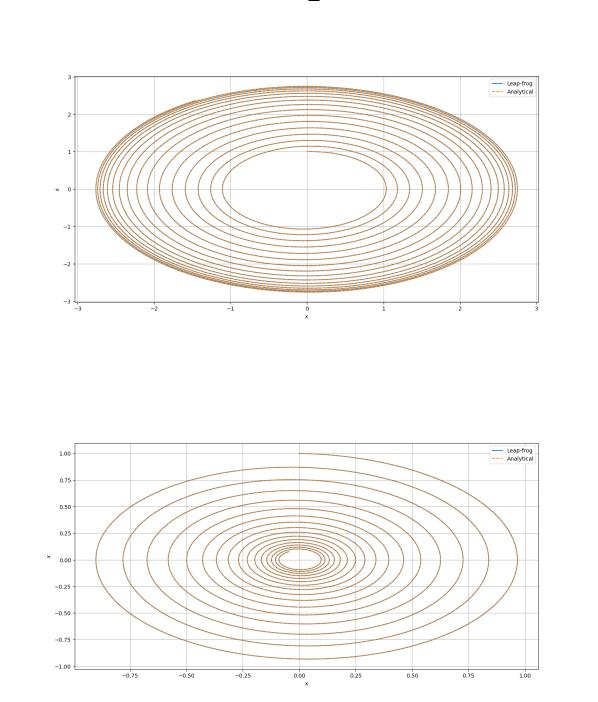
Для решения уравнения численно, будем использовать метод Верье (Leap-frog). Предварительно приведем исходное уравнение из (1) к нормальной системе дифференциальных уравнений:
(
x˙ = v,
v˙ = ϵ v − v63 − x.
Рис. 1: Фазовый портрет при ϵ = 0.05
Рис. 2: Фазовый портрет при ϵ = −0.05
4
