10669

100

где mβ – СКО измерения углов; αi – дирекционные углы направлений засечки; [q2] – сумма квадратов градиентов сторон засечки; qз – замыкающая квадратического полигона; φʹ – румб, по величине и названию которого вычисляют дирекционный угол φ большой полуоси подеры.

В свою очередь градиенты и замыкающую вычисляют по формулам:

где Si – длины сторон засечки, которые могут быть определены графически со схемы засечки; ρ" = 206265".

Необходимые данные для вычислений по формулам (74, 75) приведены в табл. 34.

В результате вычислений при mβ = 10″ получены следующие значения: qз = 237,39 с2/см2 , А = 0,74 см, В = 0,49 см, φ = 4°14'. Следует отметить, что такие аргументы как qз и φ могут быть найдены путём элементарных графических построенийm так называемого квадратического полигона Т–1'–2' со сторонами | , дирекционные углы которых 2αi. В этом полигоне Т–2' = qз, а её дирекционный угол равен 2φ.

По формулам (73), приняв, например, t = 2, вычисляем элементы результирующей подеры, характеризующей ошибку определения полного кре-

один из них (рис. 72). Проводим через точку Т прямую, дирекционный угол которой равен 4°14'. На ней откладываем в выбранном масштабе отрезки

М – средней квадратической (круговой, радиальной) ошибке. В точке е восстанавливаем перпендикуляр ав к большой полуоси подеры, причём Те = еа = ев = М/2. По точкам а, 2 и в находим центр окружности О, а также симметричный ему О1. Проведя окружности радиусом О–2 = О1–1 и плавно соединив их с точками 3 и 4, получаем подеру. При неизменной методике на-

101

блюдений в каждом цикле такие вычисления и построения достаточно выполнить один раз.

Из других способов построения подеры отметим механический способ с помощью приборов типа «Подерограф» или на ПК с использованием специальной программы.

Оценка точности определения полного крена с помощью подеры осуществляется следующим образом. Пусть в одном из циклов наблюдений был определён полный крен К = 5 см с дирекционным углом 36°. Проводим линию ТК = 5 см под углом 36° к оси х и измеряем отрезок Т–i , который в масштабе построений оказался равным 2,2 см. Следовательно, полный крен в данном цикле измерений был определён с ошибкой 2,2 см.

В общем случае с заданной вероятностью можно судить о полном крене, если его величина Кi ≥ Ri, где Ri – радиус-вектор подеры по направлению крена. При Кi < Ri нельзя судить о полном крене с заданной степенью вероятности, поскольку ошибка определения превышает его величину. Следовательно, при расчётах требуемой точности измерения горизонтальных углов βI и βII необходимо исходить из величины минимального крена, который необходимо фиксировать в результате наблюдений с заданной вероятностью.

Особый интерес представляет расположение точек так называемой Е- оптимальной опорной сети (Тамутис З.П. Оптимальные методы проектирования геодезических сетей. М.: Недра, – 1979. – 133 с.), для которой подера трансформируется в круг. В этом случае ошибки точек по любому направлению будут одинаковы. Из формул (74) видно, что А = В в том случае, если qз = 0. Эта задача может быть решена различными способами [126], причём наиболее просто с помощью построения и анализа квадратического полигона.

Одним из способов является выбор соответствующего расположения опорных пунктов. Так, подера однократной угловой засечки трансформируется в круг, если угол засечки равен 90°, а стороны засечки одинаковы. В этом случае точка 2' квадратического полигона Т–1'–2' совпадает с точкой Т, следовательно qз = 0.

Если наблюдения следует производить более чем с двух пунктов, то на плане необходимо наметить возможные направления засечки и определить их дирекционные углы. Затем на схеме провести через точку Т линии под двойными дирекционными углами. Варьируя расстояния (квадраты градиентов), число и сочетание направлений, добиваются замкнутого квадратического полигона. По квадратам градиентов определяют длины сторон засечки.

Другим способом Е-оптимизации является включение в сеть дополнительных измерений. Например, если положение некоторых опорных пунктов фиксировано, то по длине и направлению замыкающей квадратического полигона можно вычислить параметры дополнительного направления засечки для включения его в наблюдения. В нашем примере подера трансформирует-

102

ся в круг, если есть возможность к существующей схеме засечки добавить

ходимой точности измерения горизонтальных углов. В каждом конкретном случае специалисту, производящему наблюдения, следует исходить из заданной наименьшей величины крена, которую необходимо фиксировать с требуемой степенью достоверности. Тогда, приняв радиус трансформированной в круг подеры равным Кmin, на основании формул (73, 74) можно определить требуемую точность измерения горизонтальных углов засечки:

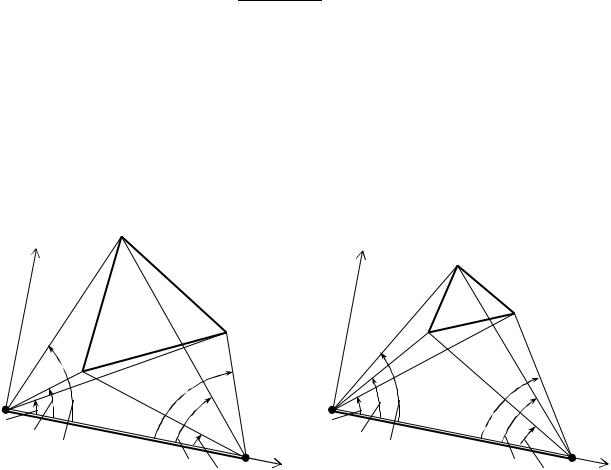
Использование способа координат для определения крена башен треугольной формы предлагается осуществлять по следующей схеме [143]. Вначале определяют координаты вершин нижнего и верхнего треугольников и находят координаты ортоцентров этих треугольников.

По координатам ортоцентров получают всю необходимую информацию. Координаты вершин треугольников могут определяться способом засечек, электронными тахеометрами или (в перспективе, согласно работе [116]) GPS-приемниками. На рис. 73 показан способ прямых угловых засечек.

Рис. 73. Схемы к определению координат нижних (а) и верхних (б) точек башни

Для выполнения способа засечек разбивают рядом с сооружением базис 1-2 известной длины Б. Точки 1 и 2 располагают произвольно на расстоянии от башни не менее полутора – двух Н (Н – высота башни) так, чтобы с них была обеспечена видимость на нижние ABC и верхние abc

точки, а углы в треугольниках засечек находились в пределах 30-120º.

104

По координата м ортоцентров OH, OB и вершин AB C, abc путём решения обратных геодезических задач определяют величину крена К, его направление и угол скр учивания φ.

При необходимости координаты вершин треуголь ников и их ортоцентров могут быть пересчитаны в другую систему коорд инат по существующим формулам перехода из одной системы координат в другую.

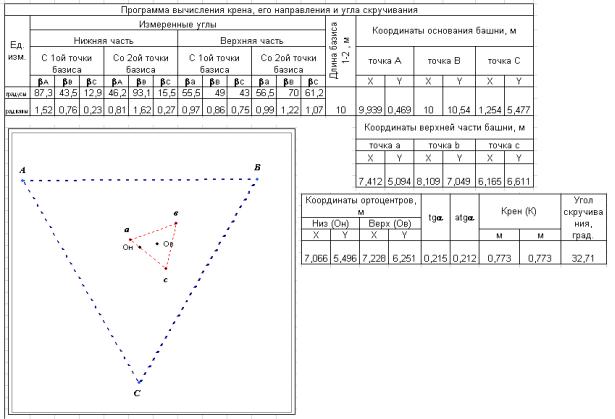
На рис. 74 прив еден пример одной из разработанных нами на базе Microsoft Exсel програм м для обработки результатов изм ерений, получаемых способом прямоугольных координат [131].

Для этого достаточно ввести в ПК длину базиса Б и 12 измеренных углов. Программа вычисляет координаты каждой вершины треугольников ABC и abc, координаты ортоцентров, величину крена и его направление и дает геометрическую интерпретацию положения верхнего тр еугольника относительно нижнего и их ортоцентров.

Рис. 74. Программа для вычисления крена башни треугольной формы и его геометрической и нтерпретации

В работе [27] т акже описана в Excel программа вычисления по известным формулам результатов измерения прямой угловой засечкой геометрии высоких стальных тр ёхгранных сооружений с одновременной геометрической интерпретацией крена, непрямолинейности отдельных элементов сооружения и его кручения.

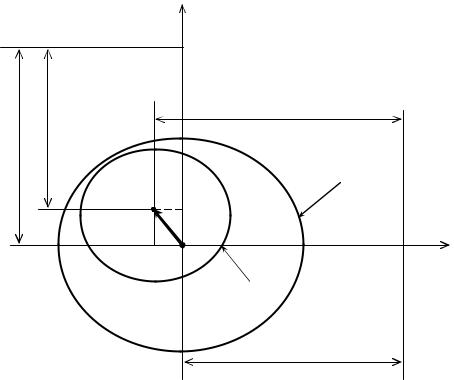
Крен трубы К и его направление (рис. 75) можно также найти путём простых графических построений. Для этого достаточно на осях прямоуголь-

= b; х = b, у2 = 0; х2 = 0, у2 = b; х2 = b, у2 = 0.

В соответствии с этим было выполнено знаковое моделирование [159], где в качестве засечки фигурировал равносторонний треугольник со стороной равной 150 м (рис. 76).

уТ3 β2

Т3

2

Рис. 76. Оптимальные варианты ориентирования базиса засечки

Для этого на базе Microsoft Exсel для любой координатной системы была разработана программа, в которой достаточно ввести в ПК значения координат точек базиса засечки и дирекционных углов двух сторон этой засечки, по которым программа вычисляет координаты точки Т. Полученные результаты моделирования представлены в табл. 35.

107

Координаты точек Т1, Т2, Т3 и Т4 на рис. 76 были также определены графическим способом, которые полностью совпали с таковыми в табл. 35.

где верхние знаки перед коэффициентом b (плюс или минус) относятся к ва-

Причём, если сооружение круглого сечения, то визирование рекомендуется выполнять по двум касательным (слева Л и справа П) к верхнему и нижнему сечению, получая два значения βЛ и βП. Средние значения β = (βЛ + βП)/2 из этих измерений принимают за направление соответственно на центр верхнего и нижнего наблюдаемого сечения.

В случае, относящемуся к рис. 76, СКО координат в зависимости от ва- рианта будут равны: ¨.,1 = 0,866 ©, у.,1 = 0,5 ©,

Однако формулы (82) дают лишь приблизительную оценку точности, поскольку они не учитывают СКО угловых измерений. В общем случае, исследуя формулы (81) с позиций теории ошибок с использованием ошибки функции общего вида, можно получить формулы оценки точности координат точки Т, которые будут иметь сложный вид. Вместо этого рекомендуется использовать методику геометрической интерпретации ошибки положения точки Т изложенную в монографии [126].

Как было отмечено выше, сущность этой методики заключается в том, что ошибка определения координат точки Т наиболее полно характеризуется подерой эллипса СКО, элементы которой А, В и φ вычисляют по формулам (74) и (75). Исходные данные и результаты вычислений по этими формулам для однократных засечек на рис. 76 при принятом значении mβ,α = 10" приведены в табл. 37.

Для этого на базе Microsoft Exсel была разработана программа, в которой достаточно ввести в ПК значения дирекционных углов и длин сторон за-

Большая полуось подеры А всегда располагается внутри острого угла засечки γ = α1 – α2. Если угол засечки тупой, то А располагается внутри острого угла, являющегося дополнением γ до 180°. В то же время при определении румба φʹ по формуле (74) для всех четырёх вариантов на рис. 76 будем получать положительный или отрицательный нуль (графа 11 табл. 37). Наглядный переход от такого нуля к удвоенному дирекционному углу большой полуоси 2φ в градусной мере можно получить путём элементарных графиче-

109

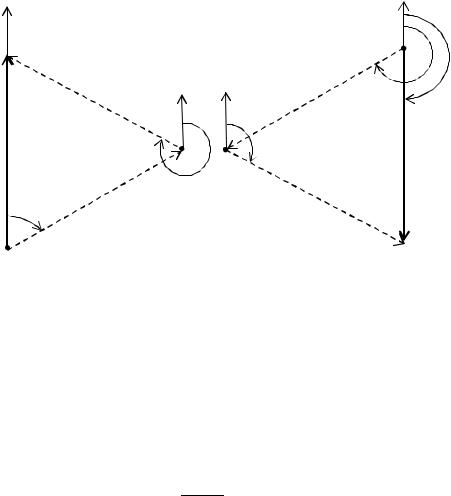
ских построений квадратического полигона Т–1 ʹ–2 ʹ со сторонами m| , дирекционные углы которых 2αi (рис. 77).

В таком полигоне Т–2 ʹ = qз является замыкающей полигона, а её дирекционный угол равен 2φ, что наглядно иллюстрируется на рис. 77. Причём замыкающая всегда имеет направление от определяемой точки Т к конечной

Рис. 77. Квадратические полигоны однократных засечек для вариантов 1,3 (а) и 2,4 (б)

Следует подчеркнуть, что периметр полигона П = [m| ] и его замыкающая qз обладают важными свойствами. Во-первых, они могут быть использованы для определенияm полуосейm А и В эллипса СКО или его подеры, а проекции замыкающей ¨ и « на оси координат – для вычисления дирекционного угла φ большой полуоси:

Во-вторых, зная периметр полигона и его замыкающую, можно вычислить радиус R и эксцентриситет e так называемой окружности СКО с внутренним или внешним эксцентриситетом, которая была в своё время предложена нами [126]. Её отличительной особенностью является то, что она может с успехом заменить такие, вообще говоря, довольно сложные по конфигурации эллипс или подеру, позволяя в то же время получать наглядно практически любую информацию о погрешности положения определяемого пункта.