
10365
.pdf71
l |
|
M |
0 |
|
M |
0 |
|
l |
|
Q |
0 |
Q |
0 |
|
|
l |
|
N |
0 |
N |
0 |
|
|
|
|
||||||
mn |
|
m |
|
|
n |
dS |
|
m |
n |
dS |
|
|
|
m |
n |
dS |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
0 |
|
|
EI |
0 |
|
|
GA |
|
|
|
0 |
|
|
|
|
EA |
|
|
|
|
|
|
|||||||||
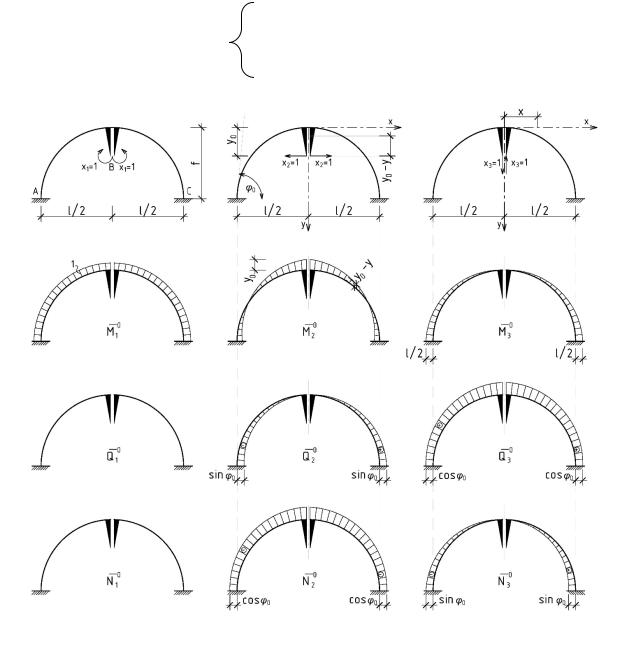
Для их |
вычисления |
построим |
эпюры |
|
|
0 |
, |
|
0 |
, |
|
0 |
в основной системе от единичных |
||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||
|
M |
Q |
N |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
i |
|
|
|
i |
|
||||
неизвестных (см. рис. 9.5).
Из рассмотрения рис. 9.4в видно, что уравнения эпюр от единичных лишних неизвестных имеют следующий вид:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
10 1; |
|
|
|
M |
20 1 (y0 y); |
|
|
|
|
|
M |
30 1 x , |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где y0 – длина консолей. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0; |
|
|
|
|
|
|
|
|
|
20 |
|
cos ; |
|
|
|
|
|
|
30 sin ; |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N10 |
|
|
|
|
N |
N |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0; |
|
|
|
|
|
|
|
|
|
0 |
|
sin ; |
|
|
|
|
|
|
0 cos . |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
Q |
|
|
|
Q |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Из приведенных на рис. 9.5 |
эпюр видно, что: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
- эпюры |
|
|
|
|
|
|
|
0 |
и |
|
|
|
|
|
|
0 |
, |
|
|
|
|
|
0 |
|
|
и |
|
|
|
0 - |
|
симметричны; |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
M |
|
M |
|
|
|
|
|
N |
|
Q |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
- эпюры |
|
|
|
|
|
0 |
, |
|
|
0 |
|
|
|
|
|
|
и |
|
|
|
|
0 |
|
|
- обратно симметричны; |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
M |
N |
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
- эпюры |
|
|
|
0 |
|
|
|
и |
|
|
|
|
0 |
|
- |
|
|
|
нулевые по всей длине арки. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Q |
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Следовательно, побочные перемещения 13 и |
|
23 |
будут равны нулю. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Подберем длину консоли y0 |
|
|
исходя из условия, чтобы и третье побочное переме- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
щение |
12 |
обращалось в ноль, т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
l |
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
l |
|
0 |
|
|
0 |
|
l |
|
|
0 |
|
|
0 |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
M |
M |
|
|
|
|
|
|
|
|
|
|
Q |
Q |
|
|
|
|
|
|
|
|
N |
N |
M |
M |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
12 |
|
|
1 |
|
|
|
|
|
|
2 |
dS |
1 |
|
|
|
2 |
dS |
|
1 |
|
|
2 |
dS |
1 |
|
2 |
dS 0. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
GA |
|
|
|
0 |
|
|
|
EA |
|
|
0 |
|
|
EI |
||||||||||||||||||||||||||||||||||
Подставим вместо |
|
10 |
|
и |
|
|
|
|
|
|
|
|
20 |
|
|
их выражения (см. выше). Тогда получим: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
M |
|
|
|
M |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B 1 (y y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B dS |
|
B y dS |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2A |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
dS 0 |
|
или |
|
|
|
y0 A |
|
|
A |
|
|
0 . |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EI |
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
I |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
B |
|
I0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y dS |
|
|
|
|
y |
dS |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
I |
|
|
A |
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Следовательно, |
|
|
|
|
|
|
|
y0 |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
B |
I0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dS |
|
|
|
|
|
|
dS |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
I |
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
I0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Если рассматривать |
|
dS |
как приведенную длину арки или приведенный контур |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
B |
|
I0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
арки, а |
y0 |
dS |
|
|
|
|
|
|
как статический момент приведенного контура арки, то y0 будет |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
A |
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
представлять собой координату центра тяжести приведенного контура арки. Именно вследствие этого, точку “B” (см. рис. 9.4б) называют упругим центром.
Таким образом, если концы консолей совместить с упругим центром “B”, то и пе-
ремещения 12 обратятся в ноль. Канонические уравнения метода сил примут в этом слу-
чае следующий вид:
72
11 x1 01P 0;
22 x2 02P 0;
33 x3 03P 0.
Рис. 9.5
Задания для самостоятельной работы.
Литература: [2, гл. 3];
Вопросы для самопроверки:
1.От каких факторов зависит очертание оси арок ?
2.Перечислите виды статически неопределимых арок.
3.Выбор расчетной схемы и метода расчета статически неопределимых арок. 4.Особенности расчета двухшарнирных и бесшарнирных арок.
73
10. Метод конечных элементов
10.1. Задачи, решаемые методом конечных элементов
Метод конечных элементов является одним из наиболее распространенных методов решения задач строительной механики и механики деформируемого твердого тела. Сущность метода состоит в том, что заданная система расчленяется на отдельные элементы конечных размеров. Для стержневой системы конечными элементами могут быть стержни или части стержней, для двухмерных областей – прямоугольные или треугольные конечные элементы; для трехмерных областей – тетраэдры или параллепипеды . Не зависимо от вида, каждый элемент сохраняет все физические и геометрические свойства заданной расчетной схемы. При этом форма конечных элементов должна быть удобна для исследования их напряженно-деформированного состояния под действием внешних воздействий и сил взаимодействия между соседними элементами.
Получая решение для отдельного конечного элемента и объединяя его с другими конечными элементами в единую заданную систему в соответствии с условиями сопряжения конечных элементов – равновесия, равенства деформаций и перемещений в узловых точках, соединяющих отдельные элементы и ряда других, - будем иметь возможность характеризовать напряженно-деформированное состояние расчетной схемы.
Т.е. при построении математической модели (основной системы) геометрия конструкции представляется набором конечных элементов очень простой формы. Изменение перемещений и напряжений внутри одного элемента моделируется также достаточно простыми функциями – линейными или квадратичными. При рассмотрении соединений конечных элементов действующие между ними напряжения представляются эквивалентными сосредоточенными силами (и иногда моментами), приложенными в точках соединения
– узловых точках. Соответственно смещения этих точек – степени свободы, используются для описания перемещений элемента. К узловым силам приводятся также внешние распределенные нагрузки, действующие на поверхности тела. Закрепление границ тела также сводится к закреплению узловых точек. Таким образом, расчетная модель становится дискретной.
Решение задачи может быть выполнено в форме метода сил, когда за неизвестные принимаются силы взаимодействия между конечными элементами в местах их соединения, или в форме метода перемещений – когда за неизвестные принимаются перемещения узлов, соединяющих элементы. В методе сил неизвестные силы должны обеспечивать равенство перемещений конечных конечных элементов в узлах, а в методе перемещений неизвестные перемещения должны удовлетворять условиям равновесия узлов. Метод конечных элементов в форме метода перемещений является более удобным по сравнению с другими, потому он получил наибольшее распространение.
Чаще всего метод конечных элементов используется для расчета континуальных систем - пластин, плит, оболочек, массивов и систем, состоящих из них. Но его можно применять и к расчету стержневых систем, которые и будем рассматривать в настоящем курсе.
74
10.2. Применение МКЭ к расчету стержневых систем. Матрица жесткости стержне-
вого конечного элемента.
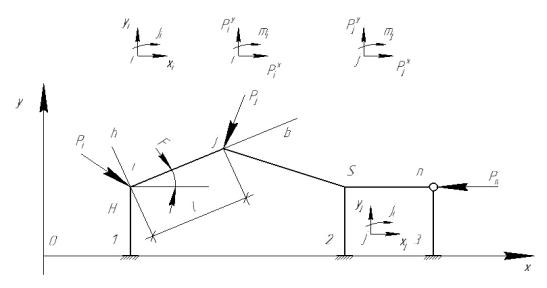
Рассмотрим стержневую систему – раму, находящуюся под действием узловой нагрузки и состоящую из “m” прямолинейных стержней постоянного по длине поперечного сечения, соединенных друг с другом “n” шарнирами или жесткими узлами, а с основанием - опорными связями (рис. 10.1).
Рис.10.1.
Введем две системы координат: общую XOY и местную .
Рассмотрим конечный элемент – стержень i j (в общей системе координат или nk в местной системе координат), длиной l, и выразим для него зависимости между перемещениями и нагрузками в общей и местной системах координат до и после его деформа-
ции. Координаты стержня до деформации x/ , y/ , x/ , |
y/ . После деформации координаты |
|
i |
i j |
j |
получили приращение xi , yi , xj , yj . |
|
|
Составим вектор перемещений концов стержня в общей системе координат: |
||
z xi yi i xj yj j |
|
zj , |
zi |
||
где xi ... j |
- линейные и угловые перемещения узлов стержня в общей системе координат. |
||||
Вектор перемещений концов стержня в местной системе координат будет: |
|||||
|
|
|
z* un vn n uk vk k |
|
|
|
|
|
zн* zk* , |
||
где un ...vk |
- линейные перемещения концов стержня в местной системе координат (вдоль |
||||
осей и ). |
|
|
|
|
|
Составим зависимость между векторами z и z*. Для этого выразим проекции пе- |
|||||
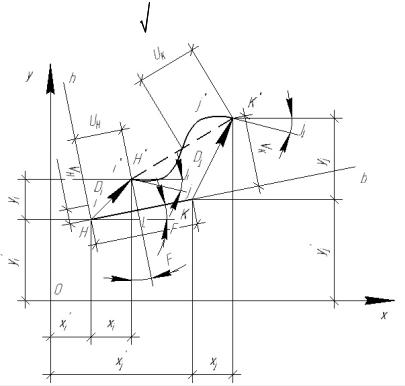
ремещения начала стержня i (рис.10.2)на оси координат: |
|||||
|
un |
xi |
cos yi |
sin ; |
. |
|
vn |
yi |
cos xi |
sin xi |
|
|
sin yi cos |
||||
n i
|
|
|
|
|
|
75 |
|
|
|
|
|
|
Используя эти зависимости, |
получим: |
|
|
|
|
|
|
|||||
|
|
|
cos |
sin |
0 xi |
|
|
|
|
|||
* |
|
|
|
sin |
cos |
|
|
|
|
|
|
(10.1) |
zн |
un vn n |
|
0 yi |
|
с zi . |
|||||||
|
|
|
|
0 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
Аналогично, для конца стержня: |
|
|
|
|
|
|
|
|||||
|
|
|
cos |
sin |
0 xj |
|
|
|
|
|||
* |
|
|
|
|
cos |
|
|
|
|
|
|
(10.2) |
zk |
uk vk k |
sin |
0 yj |
с |
zj . |
|||||||
|
|
|
|
0 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
В этих выражениях матрица с формируется по координатам узлов i и j в общей системе координат.
|
|
|
|
|
x/ |
x/ |
y/ |
y/ |
||
|
|
2 |
2 |
|
||||||
Длина стержня: l |
x/j xi/ |
y/j yi/ |
|
, cos |
j |
i |
; sin |
j |
i |
. |
|
|
|
|
|
||||||
|
|
|
|
|
|
l |
|
l |
||
Рис.10.2
Объединяя выражения (10.1) и (10.2), получим для стержня ij :
z* c z |
, |
|
|
|
(10.3) |
|
где: |
0 |
|
|
|
||
с |
|
|
|
|||
|
|
|
- матрица преобразований. |
(10.4) |
||
с |
|
|||||
0 |
с |
|
|
|
|
|
|
|
|
|
|
|
|
Умножая обе части (10.3) на с : |
с z* с c z |
, получим: |
||||
z c |
z* , |
|
(10.5) |
|||
|
76 |
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|||||||
|
|
0 |
1 |
0 |
0 |
0 |
0 |
|
|
так как с с E - единичная матрица: |
E |
0 |
0 |
1 |
0 |
0 |
0 |
|
. |
|
|
0 |
0 |
0 |
1 |
0 |
0 |
|
|
|
|
0 |
0 |
0 |
0 |
1 |
0 |
|
|
|
|
0 |
0 |
0 |
0 |
0 |
1 |
|
|
Выражения (10.3) и (10.5) позволяют осуществить переход от значений перемещений узлов стержня в местной системе координат к значениям перемещений этих узлов в общей системе координат и наоборот.
Аналогично составим выражения узловых сил по концам стержня в местной P* и в
общей P системах координат:
|
|
|
|
P* Pн Pн mн Pк Pк mк |
; |
||
|
|
|
, |
P Pix Piy mi Pjx Pjy mj |
|
||
и зависимости, с помощью которых осуществляется их взаимное преобразование, анало-
гичные (10.3) и (10.5):
|
|
|
|
(10.6) |
P* C P ; |
P C |
P* . |
||
Составим зависимость, которая выражала бы связь между узловыми нагрузками, приложенными к конечному элементу, и его узловыми перемещениями. Это можно получить, рассматривая равновесие конечного элемента и используя в качестве условия равновесия систему канонических уравнений метода перемещений:
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rik |
zk Ri,p |
0, |
(i 1,2,...,n), |
(10.7) |
|||||||
|
|
|
|
|
к 1 |
|
|
|
|
|
|
|
|
|
|
|
которая в местной системе координат может быть представлена в виде: |
||||||||||||||||
|
|
|
|
|
|
|
|
* |
* |
|
* |
. |
|
|
|
(10.8)_ |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
Rz |
z |
Rp 0 |
|
|
|
|||||
В уравнении (10.9) обозначено: |
|
|
|
|
|
|||||||||||
|
|
|
|
|
r11 |
r12 |
r13 |
r14 |
r15 |
r16 |
|
|
||||
|
|
|
|
|
r |
|
... ... ... |
... |
r |
|
|
|
||||
|
|
|
|
|
|
21 |
|
|
|
|
|
26 |
|
|
|
|
|
|
* |
|
* |
r31 ... ... ... |
... |
r36 |
|
___ |
|
||||||
|
|
|||||||||||||||
Rz |
k |
|
r |
|
... ... ... |
... |
r |
|
|
(10.9) |
||||||
|
|
|
|
|
|
41 |
|
|
|
|
|
46 |
|
|
|
|
|
|
|
|
|
r |
|
... ... ... |
... |
r |
|
|
|
||||
|
|
|
|
|
|
51 |
r |
r |
r |
r |
56 |
|
|
|
||
|
|
|
|
|
r |
r |
|
|
|
|||||||
|
|
|
|
|
|
61 |
|
62 |
63 |
64 |
65 |
66 |
|
|
|
|
матрица жесткости стержневого конечного элемента в местной системе координат. Каж-
дый элемент rmn этой матрицы представляет собой реакцию, возникающую по направле-
нию связи “m” от единичного перемещении связи “n”; при этом перемещения всех других связей, кроме связи “n”, равны нулю.

77
|
z1 |
uн |
|
|
|
|
|||||
|
z |
2 |
|
v |
н |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
z |
|
|
|
|
|
|
|
|
|
* |
3 |
|
|
н |
|
вектор перемещений в местной системе координат |
|||||
z |
z |
|
u |
||||||||
|
|
4 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|||||||
|
|
|
к |
|
|
|
|||||
|
z |
|
|
v |
|
|
|
|
|
||
|
|
5 |
|
|
к |
|
|
|
|
||
|
z |
|
|
|
к |
|
|
|
|
||
|
|
|
6 |
|
|
|
|
|
|
||
вектор перемещений в общей системе координат
Вектор R*p можно выразить через узловую нагрузку, рассматривая равновесие уз-
лов рамы (R*p = P* ).
С учетом принятых обозначений окончательно получим:
|
* |
* |
P |
* |
, |
(10.10) |
k |
|
z |
|
- основное соотношение между узловыми нагрузками и перемещениями начального и конечного сечений стержневого конечного элемента в местной системе координат.
Преобразуем выражение (10.10) для общей системы координат, умножая обе части
уравнения на с :
|
c |
|
k |
|
|
|
|
|||
|
|
c z |
c |
c P |
||||||
|
|
|
|
|
|
* |
|
|
|
|
|
|
k |
|
|
|
E |
|
|||
где: |
|
k = c |
k* c |
(10.11) |
||||||
|
|
|
|
|
|
|
|
|
|
|
-матрица жесткости стержневого конечного элемента в общей системе координат;
E - единичная матрица.
Тогда: |
k z P |
(10.12) |
- основное соотношение между узловыми нагрузками и перемещениями начального и конечного сечений стержневого конечного элемента в общей системе координат.
Матрицы жесткости основных стержневых конечных элементов в местной системе координат.
Составим матрицу жесткости стержневого конечного элемента, используя значения реактивных усилий метода перемещений и учитывая продольную деформацию стержня.
78
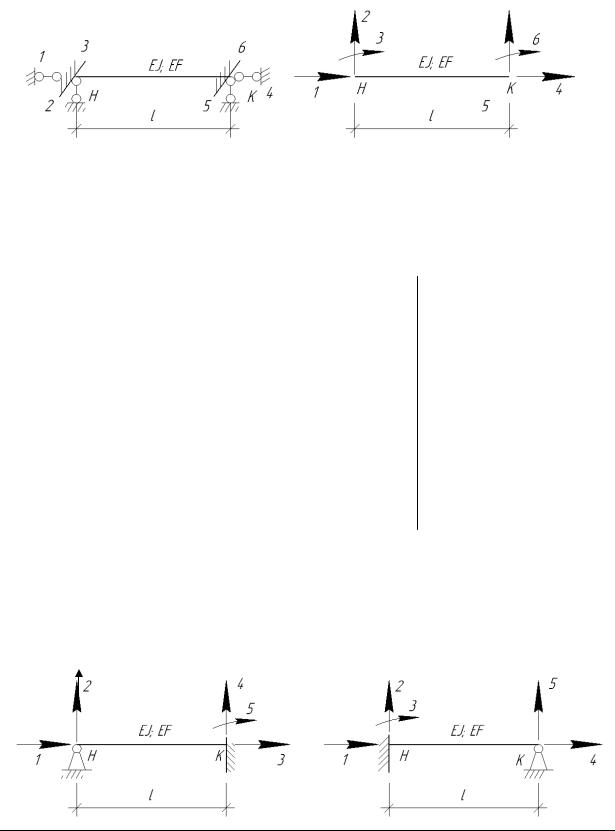
Стержень с жестко защемленными связям (см. рис. 10.3а и 10.3б)
Рис. 10.3а) и б)
Матрица жесткости стержневого элемента с жестко защемленными концами получается следующего вида (рис. 10.3б)
|
|
|
|
EF |
|
0 |
|
|
0 |
|
|
EF |
0 |
|
|
0 |
|
|||||||||||||
|
|
|
|
|
l |
l |
||||||||||||||||||||||||
|
|
|
|
|
12EI |
|
|
6EI |
|
|
|
|
|
12EI |
|
|
6EI |
|||||||||||||
|
|
|
0 |
|
|
0 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
l3 |
|
l2 |
l3 |
l2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
0 |
|
|
6EI |
|
|
4EI |
|
0 |
|
|
|
6EI |
|
|
2EI |
|
|||||||||||
|
* |
|
|
l2 |
|
|
l |
|
|
|
l2 |
|
|
l |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
EF |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
EF |
0 |
|
|
0 |
|
|
0 |
|
|
0 |
|
|||||||||||||||
|
|
l |
|
|
|
|
|
l |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
12EI |
|
6EI |
|
|
|
12EI |
|
6EI |
|||||||||||||||
|
|
|
0 |
|
|
|
0 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
l2 |
|
|
|
|
|
l3 |
|
|
|
l2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
l3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
0 |
|
|
6EI |
|
|
2EI |
|
0 |
|
|
|
6EI |
|
|
4EI |
|
|||||||||||
|
|
|
l2 |
|
|
l |
|
|
|
|
l2 |
|
|
l |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Стержень с одним защемленным концом, а другим шарнирным (см. рис. 10.4)
Рис.10.4.а) и б)

79
Для стержня с закреплением «шарнир-жесткий» (рис. 10.5а):
|
|
|
|
EF |
|
0 |
|
|
EF |
0 |
|
0 |
|
|||||||||
|
|
|
|
|
l |
l |
||||||||||||||||
|
|
|
|
|
|
3EI |
|
|
|
|
|
3EI |
|
|
3EI |
|||||||
|
|
|
0 |
|
|
0 |
|
|
|
|||||||||||||
|
|
|
|
|
|
l3 |
l3 |
l2 |
||||||||||||||
|
|
|
|
|
EF |
|
|
|
EF |
|
|
|
|
|
||||||||
|
* |
|
|
0 |
|
|
0 |
|
0 |
|
||||||||||||
|
l |
|
|
|
l |
|||||||||||||||||
k |
|
|
|
|
|
3EI |
|
|
|
3EI |
|
|
3EI |
|
||||||||
|
|
|
0 |
|
|
0 |
|
|
|
|||||||||||||
|
|
|
|
l3 |
|
|
|
l3 |
|
|
l2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
0 |
|
|
3EI |
0 |
|
|
3EI |
|
|
3EI |
|
||||||||
|
|
|
|
l2 |
|
|
|
l2 |
|
|
l |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для стержня с закреплением «жесткий-шарнир» (рис.10.5б):
|
|
|
|
EF |
|
|
|
0 |
|
|
0 |
|
|
EF |
0 |
|
||||||||
|
|
|
|
|
l |
|
|
|
|
l |
||||||||||||||
|
|
|
|
|
|
3EI |
|
|
3EI |
|
|
|
|
3EI |
||||||||||
|
|
|
0 |
|
|
|
0 |
|
|
|||||||||||||||
|
|
|
|
|
l3 |
|
|
l2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l3 |
||||
|
* |
|
0 |
|
|
3EI |
|
3EI |
|
0 |
|
|
3EI |
|
||||||||||
|
|
l |
2 |
|
|
|
l |
|
|
|
l |
2 |
|
|||||||||||
k |
|
|
|
|
|
|
|
|
|
EF |
|
|
|
|
|
|||||||||
|
|
|
|
EF |
|
|
0 |
|
|
0 |
|
|
0 |
|
||||||||||
|
|
l |
|
|
|
|
|
|
|
l |
|
|||||||||||||
|
|
|
|
|
|
|
3EI |
|
3EI |
|
|
|
|
3EI |
|
|||||||||
|
|
|
0 |
|
|
|
0 |
|
|
|||||||||||||||
|
|
|
l3 |
|
|
l2 |
|
|
|
l3 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Матрица жесткости всей системы
Используя зависимости между узловыми нагрузками и перемещениями стержневого конечного элемента, составим матрицу жесткости всей системы.
Вектор узловых внешних сил в общей системе координат:
|
|
|
|
|
, |
P |
P1,...,Pi,...,Pn |
|
|||
где: |
|
Pix Pi y mi |
|
|
|
Pi |
- вектор внешних сил в узле i в общей системе координат. |
||||
Составим вектор узловых перемещений всех узлов рамы в общей системе координат:
|
|
|
|
|
z |
z1 |
,...,zi |
,...,zn , |
|
где: zi xi yi i - вектор узловых перемещений узла i в общей системе координат.
Составим условие равновесия произвольного узла i , используя (10.12) :
|
|
|
|
|
|
|
|
|
Pi ki1 z1 |
... kii zi |
... |
zj |
... kin zn , |
(10.13) |
|||
kij |
||||||||
где: kij - матрицы жесткости конечных элементов, сходящихся в узле i , в общей систе-
ме координат.
Аналогичные условия равновесия составим для всех «n» узлов рамы:
|
|
|
k |
|
|
|
P |
|
|||||
|
1 |
|
|
11 |
|
|
|
... |
... |
|
|||
|
|
k |
|
|
||
P |
i1 |
|||||
|
i |
|
|
|
|
|
|
... |
... |
|
|||
|
|
|
kn1 |
|||
P |
|
|||||
|
n |
|
|
|
|
|
или:
... |
k1i |
... |
... |
... |
kii |
... |
... |
... |
kni |
...
...
...
...
...
k1n |
z1 |
||
... |
|
|
|
|
... |
|
|
kin zi |
, |
||
... |
|
|
|
|
... |
|
|
|
|
|
|
knn |
zn |
||
P R z
(10.14)
(10.15)
R - матрица жесткости всей системы в общей системе координат. Элементы этой
матрицы, лежащие на главной диагонали, определяются простым суммированием по всем «e» стержням, сходящимся в «i-ом» узле, т.е.:
kss kss e .
Элементы матрицы ksc , не лежащие на главной диагонали, определяются:
- |
ksc ksc e |
- |
если узлы “s” и “c” |
соединены одним стержнем; |
- |
ksc 0 |
- |
если узлы “s” и “c” |
не соединены стержнем. |
|
Решая (10.15) определяют z - вектор узловых перемещений в общей системе коор- |
|||
динат. |
|
|
|
|
По найденным перемещениям можно выразить концевые реактивные усилия в местной системе координат для каждого конечного элемента “e”. С этой целью введем два вектора:
- |
re* rн ,rн ,rнm.rк ,rк ,rкm |
|
|
- концевые реактивные усилия в местной системе коорди- |
|||
нат; |
|
|
|
- |
re rix ,riy ,rim.rjx,rjy ,rjm |
|
|
- концевые реактивные усилия в общей системе координат. |
|||
Тогда, по аналогии с (10.3), получим:
re* c e re c e ke ze .
С учетом действия внешней нагрузки, концевые реактивные усилия в местной системе координат окончательно запишутся в виде:
re/ re* Pe* .
Задания для самостоятельной работы.
Литература: [2, гл. 11]; [4, гл. 9].
Вопросы для самопроверки:
1.Понятие о конечном элементе. Поэлементное вычисление матрицы жёсткости системы.
2.Какой общий вид имеет система уравнений МКЭ? Каковы основные процедуры формирования уравнений МКЭ?
3.Основные виды конечных элементов, применяемых в расчётах строительных конструкций.
