
10365
.pdf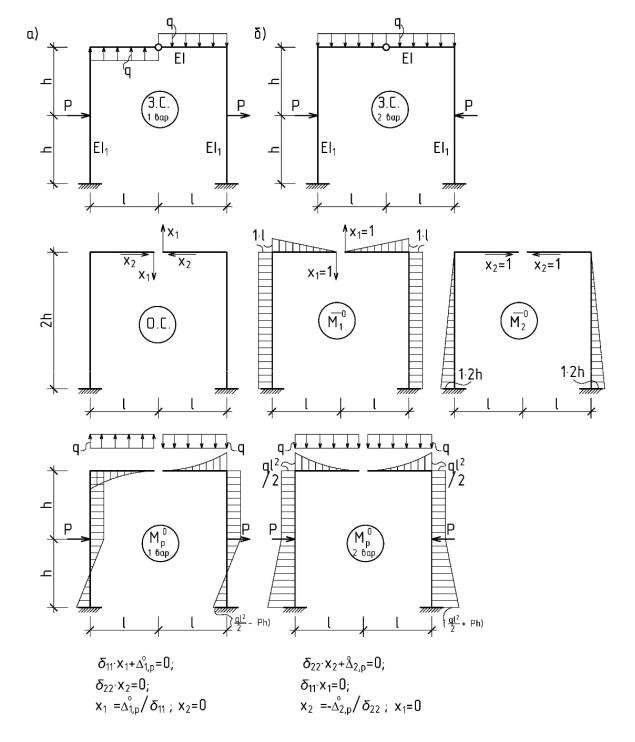
21
Рис 2.8
22
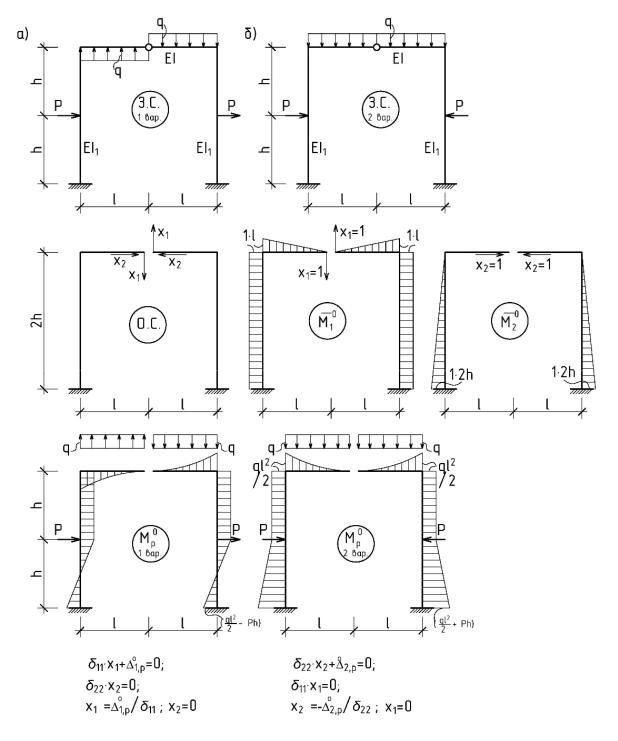
Рис 2.9
23
2.5.2. Метод группировки неизвестных при расчете симметричных рам
Из приведенного анализа вариантов решений ряда задач видно, что решение существенно упрощается при обращении ряда перемещений (побочных удельных и грузовых) в ноль. К этой же цели приводит и способ группировки неизвестных. Его основная суть заключается в том, что в симметричной системе за лишние неизвестные принимают не отдельные неизвестные, заменяющие отброшенные связи, а групповые неизвестные, выбираемые так, чтобы единичные эпюры были бы ортогональны.
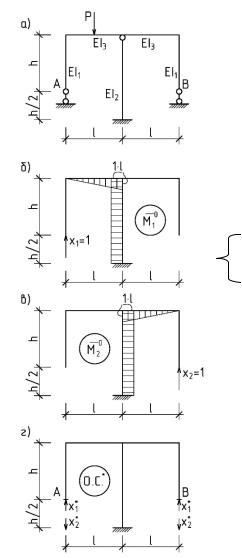
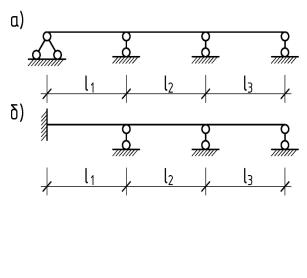
Для пояснения сказанного рассмотрим симметричную двух пролетную раму под действием несимметричной нагрузки (см. рис. 2.10).
За основную систему принимаем симметричную раму с защемлением нижнего конца средней стойки, отбрасывая крайние вертикальные опорные стержни. Первые неизвестные реакции крайних опор обозначим x1 и x2 . Они оказываются выбранными неудачно, так как эпюры изгибающих моментов, построенные, соответственно, от x1=1 и x2=1 в основной системе не являются
ортогональными. Таким образом, в этом |
случае |
|||||||
12 |
21 0и |
канонические уравнения |
будут |
|||||
являться совместными: |
|
|||||||
|
11 |
x |
12 |
x |
2 |
0 |
0; |
|
|
1 |
|
1P |
|
|
|||
21 x1 22 x2 02P 0.
Заменим первые неизвестные x1 и x2 новыми групповыми неизвестными: неизвестное x1 –
суммой неизвестных сил (x*1 x*2 ), а неизвестное x2 - разностью тех же неизвестных сил
(x*1 x*2 ). Таким образом, вместо двух сил x1 и x2
мы ввели четыре силы, определяемые двумя параметрами x*1 и x*2 , причем x*1 – значение каждой из сил симметричной группы, а x*2 – значение каждой из сил обратно симметричной группы.
24
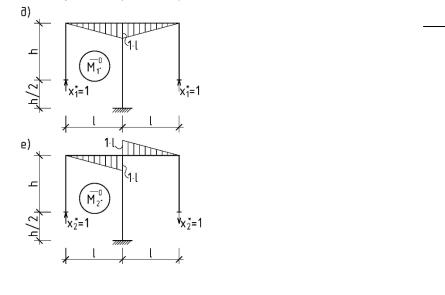
При приложении к основной системе первого
группового неизвестного |
x*1 =1, эпюра моментов |
||
___ |
единичном |
состояниии |
|
M 01 симметрична; в |
|||
|
|
|
___ |
второго группового неизвестного |
x*2 |
эпюра M 0 2 |
|
обратно симметрична. Поэтому теперь 12 21 0.
Следовательно, неизвестные в уравнениях в этом случае разделяются и канонические уравнения примут вид:
|
11 |
x* |
0 |
0; |
|
1 |
1P |
|
|
22 x*2 02P 0. |
||||
Рис 2.10 |
|
Первое уравнение выражает условие |
||
равенства нулю суммы вертикальных перемещений точек А и B, второе – разности тех же перемещений. Но так как отдельные перемещения равны нулю, то суммы и разности их тоже должны быть равны нулю. Из решения каждого уравнения определяют групповые неизвестные и далее строят эпюру моментов в заданной
___ ___
системе: M MP0 +M 01 . x*1 +M 0 2 . x*2 .
2.5.3. Использование бесконечно жестких консолей при группировке неизвестных
метода сил
Рассмотрим систему, показанную на рис. 2.11. Перережем сечение, например, ригеля в произвольном сечении и прикрепим в этом месте две бесконечно жесткие консоли. Если эти консоли каким угодно образом соединить в одно жесткое целое, например с помощью трех жестких стержней, не пересекающихся в одной точке, то условия работы полученной системы ни чем не будут отличаться от заданной. Тем не менее, это будет справедливо именно только при абсолютной жесткости консолей. В противном случае при консолях, обладающих податливостью, взаимное их скрепление не обеспечило бы взаимной неподвижности сечения ригеля в месте его перерезывания.
Наличие таких абсолютно жестких консолей удобно тем, что их использование позволяет в широких пределах варьировать выбором основных неизвестных. За основные неизвестные могут быть приняты усилия в перерезанных стержнях, а последние можно располагать на плоскости как угодно, лишь бы они не пересекались в одной точке.
В рассматриваемом примере по рис. 2.11 целесообразно перерезать сечение ригеля по оси симметрии и считать, что консоли связаны друг с другом двумя горизонтальными и одним вертикальным стержнями. Тогда эпюры от единичных неизвестных – усилия в перерезанных стержнях, - будут такими, как показаны на рис. 2.11б. На консолях эпюры показывать не имеет смысла, так как не зависимо от их вида учитывая, что жесткость консолей EI= , все интегралы на участке их длины обратятся в ноль.
Горизонтальные лишние неизвестные можно располагать на любом расстоянии от оси ригеля. Используем эту возможность следующим образом: расположим силу x1 на том
25
же уровне, на котором находится центр тяжести |
треугольной |
эпюры |
___ |
т.е. на |
||||
M 0 2 , |
||||||||
расстоянии 2.h/3 от ригеля. Тогда перемещение 12 |
будет равно нулю, так как эпюры |
|||||||
___ |
и |
___ |
|
|
|
___ |
___ |
а также |
M 01 |
M 0 2 ортогональны. Ортогональными же являются эпюры |
M 01 и |
M 0 3 , |
|||||
___ |
и |
___ |
___ |
___ |
и обратно |
симметричная |
___ |
|
M 0 2 |
M 0 3 (как симметричные |
M 01 |
и M 0 2 |
M 0 3 ). |
||||
Следовательно, все три побочных удельных перемещений обратятся в ноль и система канонических уравнений метода сил разделится на три самостоятельных уравнения:
11 x1 01P 0;
22 x2 02P 0;
33 x3 03P 0.
Задания для самостоятельной работы.
Литература: [1, гл. 5]; [2, гл. 6]; [4, гл. 4].
Вопросы для самопроверки:
1.Каким требованиям должна отвечать основная система в методе сил?
2.Как составляются канонические уравнения в методе сил, и какие требования они отражают?
3.В чем заключается физический смысл коэффициентов при неизвестных в канонических уравнениях метода сил?
4.Как определяются коэффициенты канонических уравнений метода сил?
5.Почему статическая проверка в методе сил необходимой, но недостаточной?
6.Почему внутренние усилия при силовом воздействии не зависят от абсолютных значений жесткостей, а определяются их соотношением?
7.В каком случае внутренние усилия будут зависеть от абсолютных значений жесткостей?
8.Какова последовательность расчета статически неопределимых систем методом сил?
9.В чем состоит отличие статически неопределимых систем от статически определимых систем?
10.Как определяется число лишних связей статически неопределимой системы? 11.В чем заключается физический смысл канонических уравнений метода сил?
12.Чем отличается вычисление коэффициентов при неизвестных от вычисления грузовых коэффициентов?
13.В чем заключается универсальная проверка?
14.Для чего используется постолбцовая проверка?
15.Каков алгоритм метода сил?
16.Какие способы проверки правильности расчета существуют?
26
3. Расчет неразрезных балок
3.1. Общие сведения о неразрезных балках
Неразрезной балкой называют конструкцию в виде бруса, перекрывающего два и более пролета и неразрывно связанного с опорами, нигде не прерываясь по длине шарнирами или разрезами. Характерным отличием неразрезной балки от разрезной является то, что нагрузка, расположенная в любом пролете неразрезной балки изгибает ее на протяжении всех пролетов, создавая плавную упругую линию.
Неразрезные балки экономичнее разрезных, так как при одинаковой нагрузке значения изгибающих моментов в них меньше. Недостатком неразрезных балок, как, в общем, и всякой статически неопределимой системы, является чувствительность их к неравномерной осадке опор, а также появление дополнительных напряжений при неравномерном изменении температурного режима.
Расчетная схема неразрезной балки предполагает идеальное шарнирное прикрепление ко всем промежуточным опорам и допускает абсолютную или упругоподатливую заделку только крайних опор.
Неразрезная балка принадлежит к числу наиболее распространенных конструкций. Она применяется в металлическом, железобетонном и деревянном строительстве в качестве основной части сооружения или его элемента: несущие пролетные строения мостов, переходных галерей, путепроводов; грузовые пояса подкраново-подстропильных и подкраново-стропильных ферм; подкрановые балки каркасов промышленных зданий и т.д.
3.2. Степень статической неопределимости. Основная система
Как известно, для обеспечения неподвижности стержня в плоскости требуется три опорных стержня, не пересекающихся в одной точке. Поэтому количество лишних связей неразрезной балки всегда меньше числа ее опорных связей на три единицы.
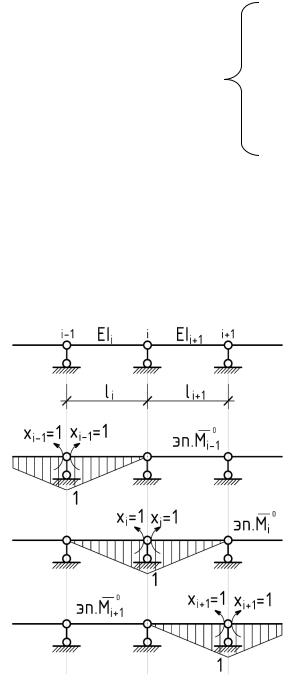
Так, например, балка, изображенная на рис. 3.1a, содержит две лишние связи, т.е. два раза статически неопределима, а балка по рис. 3.1б – три лишние связи или трижды статически неопределима.
Неразрезная балка может быть статически определимой только в одном случае: когда она имеет три опорных стержня, не пересекающихся в одной точке, не параллельных между собой и разбивающих
длину балки на два пролета – рис. 3.2.
Рис.3.1.
При выборе основной системы необходимо стремиться к тому, чтобы канонические уравнения получались наиболее простыми. Такой эффект будет иметь место в том

27
случае, когда максимальное количество побочных удельных перемещений обратятся
в ноль.
Рис.3.2.
Рассмотрим неразрезную балку, изображенную на рис.3.3a. На рис. 3.3б показана возможная основная система, полученная из заданной путем устранения лишних промежуточных опорных стержней. Именно такая основная система является первой по времени появления в литературе и содержит следующие недостатки: в каждое из канонических уравнений входят все неизвестные и не одно из побочных удельных перемещений не обращается в ноль. Каждое уравнение выражает равенство нулю перемещения точки приложения каждого из неизвестных (x1, x2, …, xn) по его
направлению в основной системе от самих
Рис 3.3
неизвестных и заданной нагрузки или, иначе, равенство нулю прогиба каждой из опор заданной системы.
При более удачном выборе основной системы для неразрезной балки можно добиться того, что множество коэффициентов (побочных удельных перемещений) обратится в ноль и при любом количестве пролетов ни одно из уравнений не будет содержать больше трех неизвестных.
3.3. Расчет неразрезных балок на внешнюю нагрузку. Уравнение трех моментов
Выберем в качестве основной системы совокупность однопролетных шарнирно опертых балок. Такая статически определимая система получается из заданной неразрезной балки (рис. 3.4a) путем устранения жесткой (моментной) связи между сечениями на каждой промежуточной опоре и замене ее шарнирной. Число отброшенных моментных связей обозначим через “n”. За неизвестные x1, x2, …, xn примем изгибающие моменты, действующие в опорных сечениях.
Так как заранее неизвестно, какой из этих моментов растягивает нижнее, а какой верхнее волокно балки, то будем считать, что все неизвестные изгибающие моменты растягивают нижнее волокно (рис. 3.4б). Если на самом деле тот или иной момент направлен в обратную сторону, то это выясниться в
Рис 3.4
28
результате реше ния системы уравнений и получения для этого момента знака минус.
Все левые части каждого из уравнений выражают собой суммарный взаимный угол поворота сечения на рассматриваемой опоре, вызываемый всеми лишними неизвестными и заданной внешней нагрузкой.
Этот угол взаимного поворота можно назвать также углом перелома упругой линии на соответствующей опоре. Из рис. 3.4б видно, что момент x1 вызывает перелом упругой линии только на опорах 1 и 2; момент x2 – на опорах 1, 2 и 3; момент x3 – на опорах 2, 3 и 4 и т.д. В свою очередь перелом на опоре 1 зависит только от моментов x1 и x2 и от внешней нагрузки, но не зависит от всех остальных лишних неизвестных. Аналогично, перелом на опоре 2 зависит только от x1, x2, x3 и от внешней нагрузки и.т.д.
Следовательно, в каждом из канонических уравнений, кроме первого и последнего, будут фигурировать только по три неизвестных, а в первом и последнем – только по два.
Эти рассуждения позволяют без всяких дополнительных вычислений переписать канонические уравнения для балки по рис.3.4б в более простой форме:
11 x1 12 x2 1P 0;
21 x1 22 x2 23 x3 2P 0;
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
i,i 1 xi 1 ii xi i,i 1 xi 1 i,P 0;
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
n 1,n 2 xn 2 n 1,n 1 xn 1 n 1,P 0.
Такие уравнения называются трехчленными, так как каждое из них содержит не более трех неизвестных. При этом, учитывая, что неизвестными являются опорные моменты (x1=M1, xi=Mi , xn-1=Mn-1), канонические уравнения называют уравнениями трех моментов.
Вычислим удельные перемещения, входящие в канонические уравнения. С этой целью построим эпюры изгибающих моментов в основной системе от единичных
значений лишних неизвестных (рис.3.5).
|
i,i |
1 |
|
1 |
|
1 l |
i |
|
1 |
|
1 |
1 |
|
|
|
|
li |
|
|
; |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
6 EIi |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
EIi |
|
|
|
|
|
|
|
|
|||||||||||||||
|
i,i |
|
1 |
|
1 l |
i |
|
2 |
1 |
|
1 |
|
|
1 |
|
1 l |
i 1 |
|
2 |
1 |
1 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
EIi |
2 |
|
|
|
|
3 |
|
|
EIi 1 |
|||||||||||||
|
|
|
li |
|
|
|
|
|
|
|
li 1 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
3 EIi |
3 EIi 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
i,i |
1 |
|
1 |
1 l |
i 1 |
|
|
1 |
1 |
1 |
|
|
|
|
|
li 1 |
. |
|
|
||||||||||||||||||||
|
|
|
EIi 1 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
6 EIi 1 |
|
|
||||||||||||||||||||
Обозначим |
|
через |
|
EI0 |
жесткость, принятую за |
|||||||||||||||||||||||||||||||||||
единичную. Тогда для i-ой промежуточной опоры каноническое уравнение примет вид:
Рис.3.5.

|
|
|
|
|
|
|
|
|
|
|
29 |
li EI0 |
Mi 1 |
2 ( |
li EI0 |
|
li 1 EI0 |
) Mi |
|
||||
|
|
|
|
||||||||
EIi |
|
|
EIi |
|
EIi 1 |
|
|||||
|
li 1 EI0 |
Mi 1 6 EI0 iP 0 . |
|
||||||||
|
|
||||||||||
|
EIi 1 |
|
|
|
|
|
|
|
|||
|
Рис.3.5. |
|
|
|
|
|
|
|
|||
Величину |
li |
EI0 |
i |
называют приведенной длиной пролета i. Тогда: |
|||||||
|
|
||||||||||
|
|
|
|
|
EIi |
|
|
|
|
||
i Mi 1 2 ( i i 1)Mi i 1 Mi 1 6EI0 iP
Это и есть уравнение трех моментов.
В том случае, когда балка имеет во всех пролетах один и тот же момент инерции, т.е.
жесткость балки по длине постоянна и равна EI, целесообразно принять EI0 EI и тогда уравнение примет следующий вид:
li Mi 1 2 (li li 1)Mi li 1 Mi 1 6 EI iP
Полученное уравнение составляется для каждой промежуточной опоры.
Для определения свободного члена уравнения трех моментов – грузового перемещений
iP , необходимо построить эпюры изгибающих моментов в основной системе от единичного неизвестного xi Mi 1 и от заданной нагрузки, расположенной в пролетах слева и справа от опоры i (см. рис. 3.6).
Тогда:
|
|
|
|
|
|
|
|
|
|
|
|
|
___ |
|
|
___ |
|
|
|||||
|
|
|
|
|
|
|
|
|
iP |
|
i a i |
|
i 1 b i 1 |
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
li EIi |
|
li 1 EIi 1 |
||||||||||
|
|
|
|
Уравнение трех моментов примет вид: |
|||||||||||||||||||
|
|
|
|
i Mi 1 2 ( i |
i 1)Mi |
|
i 1 Mi 1 |
||||||||||||||||
|
|
|
|
|
|
|
|
___ |
|
|
|
|
|
|
|
|
___ |
|
|
|
|||
|
|
|
|
6 ( |
i |
a i EI0 |
|
i 1 b i 1 EI0 |
), |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
li EIi |
|
|
|
|
|
li 1 EIi 1 |
|||||||||
|
|
|
|
или: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
i Mi 1 2 ( i |
i 1)Mi |
|
i 1 Mi 1 |
||||||||||||||||
|
|
|
|
|
|
|
|
___ |
|
|
|
|
|
|
|
|
___ |
|
|
|
|||
|
|
|
|
6 ( |
i |
a i |
i |
i 1 b i 1 |
i 1). |
||||||||||||||
|
|
|
|
|
li2 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
li21 |
|||||||
|
|
Рис.3.6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При равных жесткостях всех пролетов балки: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
___ |
|
|
|
|
___ |
|
|
|
|
|
|
|
|
||||||
li |
Mi 1 2 (li |
li 1) Mi |
li 1 Mi 1 |
6 ( |
i a i |
|
i 1 b i 1 |
). |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
li |
|
|
|
|
|
li 1 |
|
|
|
|
|
|||||||

30
Последнее выражение можно написать иначе, если обратить внимание на то (см.
|
|
|
|
|
|
|
|
___ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рис. 3.6), что произведение |
i |
a i |
Bф |
|
- |
есть правая опорная реакция пролета |
l |
i |
от |
||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
li |
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
___ |
|
|
|
|
|
|
|
|
|
фиктивной нагрузки |
i |
. Аналогично |
i 1 |
b i 1 |
= Aф |
есть левая опорная реакция пролета |
|||||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
li 1 |
|
|
|
i 1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
li 1 от фиктивной нагрузки |
|
i 1 . Тогда |
окончательно при |
равных жесткостях |
всех |
||||||||||||||||||
пролетов балки уравнение трех моментов примет вид: |
|
|
|
|
|
||||||||||||||||||
l |
i |
M |
i 1 |
2 (l |
i |
l |
i 1 |
) M |
i |
l |
i 1 |
M |
i 1 |
6 ( Bф Aф ) |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
i |
i 1 |
|
|
|
||||||||
Если нагрузка в пролете представляет собой сложное загружение, состоящее из нескольких простых, например: в пролете одновременно действуют сосредоточенная сила и распределенная нагрузка, - то фиктивные реакции можно определять как сумму
реакций, отвечающих каждой схеме загружения. |
|
|
В таблице 3.1 даны величины (6 Aф ) и |
(6 Bф ) для некоторых вариантов нагрузок. |
|
Таблица 3.1 |
|
|
|
|
|
Схема нагружения пролета |
6 Aф |
6 Bф |
|
|
|
|
P l2 u v (1 v) |
P l2 u v (1 u) |
|
q l3 |
|
q l3 |
||||
|
4 |
|
4 |
|
|||
|
|
|
|
|
|
||
|
5 |
q l3 |
|
5 |
q l3 |
||
|
32 |
32 |
|||||
|
|
|
|
|
|||
