10321

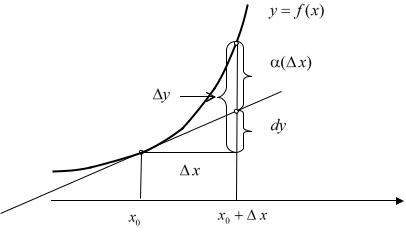
[Введите текст]

можно сделать, если данная функция дифференцируема в точке x0 . Действительно, в этом случае в точке (x0 , f (x0 )) существует касательная к гра-

жённо заменить приращением ординаты касательной dy (см. рис. 21.1)

y dy f (x0 ) x

Рис. 21.1

Таким образом, приращение функции y представлено в виде двух

Первое из них называют дифференциалом функции в данной точке и обо-

значают символом

dy f (x0 ) x .

Ввиду важности этого понятия, только что определённого кратко с помощью формулы (21.1), приведём его словесную формулировку, акцентирующую внимание на наиболее характерных свойствах дифференциала.

Дифференциалом функции в данной точке называется главная часть приращения функции в этой точке, линейная относительно приращения независимой переменной x .

Второе слагаемое (заметим, что оно может быть любого знака) представляет собой бесконечно малую величину более высокого порядка, чем

150

[Введите текст]

Другими словами, обе бесконечно малые y и dy эквивалентны. В связи

с этим дифференциал называют главной частью приращения функции. Убедимся на следующем примере, что дифференциал действительно

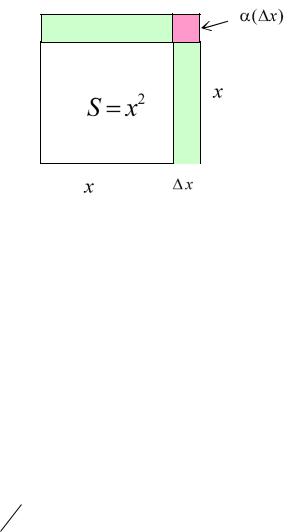
составляет «львиную» долю приращения функции. Площадь квадрата со стороной x равна S (x) x2 . Вычислим приращение этой функции

S (x x)2 x2 2x x ( x)2 .

Рис. 21.2

Из рисунка видно, что первое слагаемое, представляющее собой дифференциал, равно площади двух прямоугольников, а второе равно площади квадрата со стороной x .

Заменяя приращение функции дифференциалом, мы получаем универсальную формулу для вычисления значения функции в точке близкой к

[Введите текст]

Отметим еще раз геометрическое содержание приближённого равенства (21.2), переписав его в других обозначениях

y y0 f (x0 )(x x0 ) .

Отбрасывая в приращении функции бесконечно малую величину более высокого порядка, чем x , мы заменяем кривую в окрестности точки x0 её

касательной в этой точке, т.е. линеаризуем данную функцию, заменяя её

линейной функцией.

Заметим, что дифференциал независимой переменной равен её приращению, т.е.

Таким образом, дифференциал функции вычисляется по формуле d f (x) f (x)d x .

Отсюда получаем выражение производной через дифференциалы f (x) dd xy .

Отметим еще так называемое свойство инвариантности дифференциала. Пусть сначала имеем функцию y f (u) , где u – независимая перемен-

ная. Тогда по определению

dy f (u)du .

В случае же, когда u (x) , используя формулу производной сложной функции, получим

dy f (u) (x)dx f (u)du .

Таким образом, выражение для дифференциала не зависит от того, является ли аргумент независимой или зависимой переменной.

Дифференциалы высших порядков определяются по индукции: дифференциал n -го порядка равен дифференциалу от дифференциала (n 1) -го

порядка

d n x d (d n 1x) .

152

21.2. Правило Лопиталя. Франсуа маркиз де Лопиталь (1661-1704) ма- тематик-любитель, ученик Иоганна Бернулли, автор первого печатного учебника курса дифференциального исчисления.

Под «правилом Лопиталя» понимают один из способов вычисления некоторых пределов. Пусть речь идёт о вычислении предела отношения

[Введите текст]

Найдем предел логарифма этого выражения

Следовательно, искомый предел равен

155

[Введите текст]

Лекция 22. Исследование функций и построение их графиков

В аналитическом выражении, которым чаще всего бывает задана функция, содержится вся информация о её свойствах. График функции делает эти свойства легко обозримыми. Поэтому нужно уметь строить график функции по формуле, которой она задана. Самый простейший приём – это построение «по точкам». Однако он требует большого объёма вычислений и при этом могут быть потеряны характерные особенности исследуемой функции. Приёмы исследования, основанные на дифференциальном исчислении, позволяют именно эти особенности и уловить. Так, например, один факт существования производной функции в точке x0 даёт возможность ли-

неаризовать функцию в окрестности этой точки. Дифференцируемость функции, как мы выяснили ранее, равносильна представлению её приращения в виде

y f (x0 ) x ( x) ,

где ( x) – бесконечно малая более высокого порядка, чем x . Заменяя

мы заменяем в окрестности точки x0 кривую y f (x) касательной к ней в

этой точке. Нельзя ли это приближённое равенство превратить в точное? Такое равенство, выражающее приращение дифференцируемой функции через приращение её аргумента, было получено Лагранжем (1736-1813гг).

22.1. Формула Лагранжа имеет вид

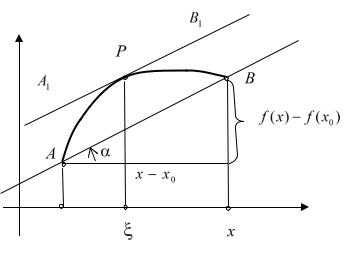
f (x) f (x0 ) f ( )(x x0 ) , x0 x . (22.1)

За знак равенства в ней мы «заплатили» тем, что не знаем точного положения точки . Эту формулу называют также формулой конечных прира-

щений.

Из (22.1) следует, что на интервале (x0 , x) существует точка , в кото-

рой

f ( ) f (x) f (x0 ) tg , x x0

156

[Введите текст]

т.е. касательная в этой точке параллельна прямой AB (см. рис. 22.1). Из рисунка видно, что является абсциссой точки P , полученной перемещением прямой AB параллельно себе. Формулу конечных приращений или формулу Лагранжа (22.1) мы будем неоднократно применять в дальнейшем.

Рис. 22.1

22.2.Признак монотонности функции. Применим формулу Лагранжа

кисследованию поведения функции на некотором промежутке (a,b) .

Напомним, что функция называется возрастающей в этом промежутке, если для любых значений x1 x2 выполняется неравенство f (x1) f (x2 ) .

Выясним, каков же признак того, что функция возрастает.

Пусть производная функции положительна во всех точках промежутка (a,b) . Для произвольных x1 x2 из этого промежутка применим формулу

Поскольку правая часть этого равенства положительна, то f (x2 ) f (x1) , т.е. f (x) – возрастающая функция. В предположении, что производная неотрицательна ( f (x) 0) , получим, что функция – неубывающая в этом проме-

жутке, т.е. f (x2 ) f (x1) .

Аналогичным образом можно получить признаки убывающей и невоз-

растающей функций: f (x) 0 и f (x) 0 .

Геометрически эти признаки означают, что в точках возрастания функции касательная к кривой составляет острый угол с положительным направлением оси абсцисс, а в точках убывания – тупой. В качестве примера найдем промежутки возрастания и убывания функции

157

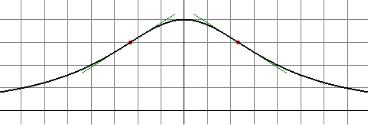
Рис. 22.2

Следовательно, в промежутке ( ,0) эта функция возрастает, а в промежутке (0, ) – убывает.

22.3. Экстремумы. Под экстремумом функции в точке понимают её максимальное или минимальное значение в некоторой окрестности этой точки. Говорят, что точка x0 – точка максимума (минимума), если в некото-

Как находить экстремумы, зная аналитическое выражение функции? Заметим, что точки экстремумов разделяют интервалы возрастания и убывания функции (точки максимумов) и наоборот (точки минимумов). Исходя из приведенных выше условий монотонности функции, естественно предположить, что в точках экстремумов производная функции обращается в ноль или не существует. Для дифференцируемых функций имеет место следующее.

Необходимое условие экстремума. Пусть функция имеет конечную производную в (a,b) и x0 – точка максимума (для определенности). Тогда

производная в этой точке равна нулю f (x0 ) 0 , т.е. касательная в точке

экстремума горизонтальна (такие точки иногда называют стационарными). Действительно, по определению производной

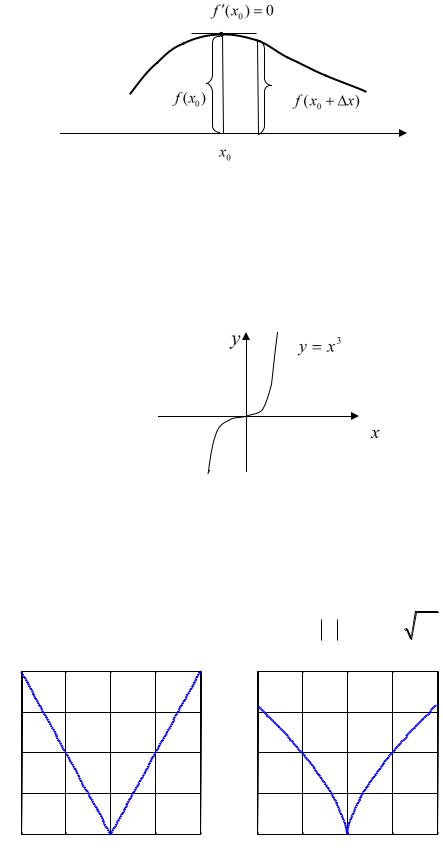
[Введите текст]

Рис. 22.3

Следующий пример показывает, что обратное утверждение не верно. Так, для функции y x3 производная в начале координат равна нулю, касательная совпадает с осью абсцисс, но экстремума в этой точке нет.

Рис. 22.4

Другие точки, в которых могут быть экстремумы, это точки, в которых производная либо не существует, либо обращается в бесконечность. В совокупности со стационарными эти точки называют критическими. Примеры