10303

Рис. 52.1

а тройной интеграл в декартовых координатах обозначается следующим образом:

f (x, y, z) в области .

Сравнивая рассуждения, проведенные при нахождении массы пространственного тела, со способом введения тройного интеграла, приходим к выводу, что

M (x, y, z)dV .

G

Свойства тройного интеграла аналогичны свойствам двойного интеграла. Следует обратить внимание на случай, когда в качестве подынтегральной функции выступает функция, тождественно равная единице

что она равна объѐму области интегрирования. Таким же, естественно, оказывается и предел интегральных сумм. Тем самым, получаем способ вычисления объѐма пространственной области с помощью тройного интеграла

dxdydz V .

Заметим, что определения всех определѐнных интегралов (начиная с обычного определѐнного интеграла по отрезку и завершая тройным интегралом) аналогичны. Они могут быть сформулированы единым образом. Вместо длины, площади или объѐма фигурирует обобщѐнное понятие «мера множества». На этом же языке можно записать общие свойства всех определѐнных интегралов.

82

52.3. Вычисление тройного интеграла в прямоугольных декарто-

вых координатах. Вычисление тройного интеграла, как и двойного, сводится к последовательному интегрированию функций одной переменной (теперь уже трижды). Для этого удобно представить тройной интеграл в виде комбинации обычного определѐнного интеграла по отрезку и двойного интеграла. Двойной интеграл, в свою очередь, заменяется повторным уже известным способом.

Снова нужно начинать с точного описания области, по которой ведѐтся интегрирование. Пусть – некоторая область в пространстве. Через D обозначим ее проекцию на плоскость xOу . Рассмотрим произвольную

ограниченной цилиндрической поверхностью с образующей, параллельной оси Oz . Еѐ характерная особенность заключается в том, что каждая прямая, параллельная оси Oz и проходящая через внутреннюю точку области

кальной цилиндрической поверхностью, проходящей через его границу,

Здесь интегрирование ведѐтся от точки входа на поверхности до точки выхода поверхности . При этом интегрировании и и элемент 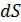постоянны.

83

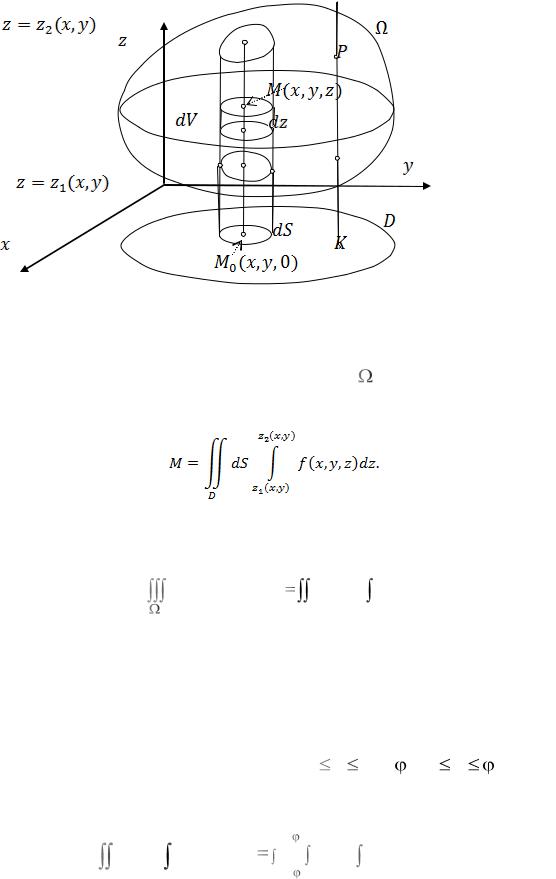
Рис. 52.2

Для того чтобы вычислить массу всего тела , нужно «просуммировать» массы всех «столбиков», подобных рассмотренному выше. Таким образом,

Это приводит нас к формуле вычисления тройного интеграла

янные величины. Затем вычисляется внешний двойной интеграл по области D .

84

Последний результат совпадает с формулой вычисления объѐма двойным интегралом, полученной ранее.

Заметим, что сходным образом можно ввести понятие пространственной области, правильной в направлении оси Ox или оси Oy . Скажем, пра-

вильная в направлении оси Ox область должна быть ограничена поверхностями x x1( y, z) , x x2 ( y, z) и цилиндрической поверхностью с обра-

зующими, параллельными оси Ox .В этом случаев формуле, аналогичной формуле (52.2), внутреннее интегрирование ведѐтся по переменной x , а двойной интеграл берѐтся по области, которая является проекцией тела на плоскость yOz .

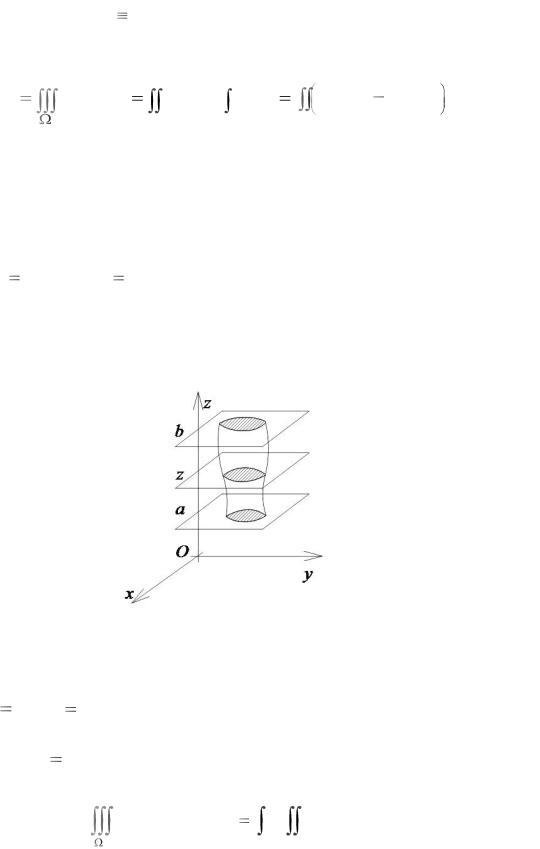
Рис. 52.3

Другой способ вычисления тройного интеграла удобно использовать для областей, располагающихся в полосе между горизонтальными плоскостями z a и z b (рис. 52.3). При этом необходимо определить, как изменяются в зависимости от переменной z сечения DZ исходной области

плоскостью z const . В этом случае получаем следующую формулу вычисления тройного интеграла:

Здесь сначала вычисляется внутренний двойной интеграл по области D , а

Z

затем – определенный интеграл по отрезку, на котором меняется переменная z . Естественно, можно записать аналогичные формулы и для другого

85

плоскости α введем полярную систему координат (r, ) с полюсом в точке O , являющейся пересечением оси L с плоскостью.

Рис. 52.5

Тогда цилиндрические координаты (r, , h) точки P будут пред-

ная поверхность r const является круговым цилиндром, что и объясняет название координат. Если ввести декартову систему координат, совместив ось Ox с полярной осью, а плоскость α – с плоскостью xOу (рис. 52.5), то

связь между декартовыми и цилиндрическими координатами запишется очевидным образом

Рис. 52.6

Цилиндрические координаты используют при рассмотрении тел вращения (круговые цилиндр, конус и т.д.), причем ось L располагают по оси вращения. Например, записанные в цилиндрических координатах уравне-

87

бой параллелепипеды. Чтобы найти элементы объѐма в цилиндрических

y

i

O

x

Рис. 52.7

Так как объѐм цилиндра равен произведению площади основания на высоту, а основанием в данном случае оказывается элемент площади в по-

лярных координатах ds rdrd , то элементарный объѐм dV rdrd dh . Поэтому формула перехода в тройном интеграле от декартовых координат к цилиндрическим приобретает вид

В качестве примера определим массу M материального полушара радиуса R с центром в начале координат, если плотность его вещества в каждой точке (x, y, z) пропорциональна расстоянию от этой точки до основания, т.е. (x, y, z) kz (рис. 52.8). В декартовых координатах верхняя по-

лусфера задается уравнением z R2 x2 y2 .

Рис. 52.8

Рассмотрим цилиндрические координаты. В них для точек полушара

89

Лекция 53. Тройной интеграл в сферических координатах. Приложения к механике

53.1. Вычисление тройного интеграла в сферических координатах.

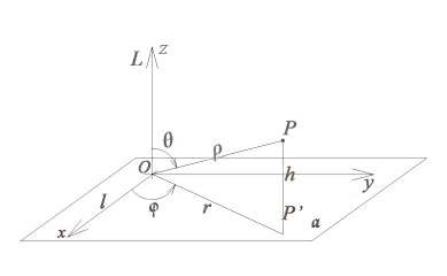
Чтобы ввести сферические координаты в трёхмерном пространстве, рассмотрим снова плоскость α и перпендикулярную ей ось L . На плоскости α введём ось l . Тогда сферические координаты (ρ,ϕ,θ) точки P будут представлять собой соответственно её расстояние ρ от начала координат (длина радиус–вектора точки P ), угол ϕ между проекцией OP′ радиусвектора точки P на плоскость α и осью l , а также угол θ между радиусвектором OP и осью L (рис. 53.1). Координатная поверхность ρ = const является сферой, что объясняет название координат.

Для описания всех точек в пространстве достаточно следующих промежутков изменения координат: 0 ≤ ρ < ∞, 0 ≤ θ ≤ π, 0 ≤ ϕ < 2π .

Введём декартову систему координат, совместив ось Ox с осью l , а плоскость xOу декартовой системы – с плоскостью α (рис. 53.1). Декар-

товы координаты точки P обозначим (x, y, z) , тогда координаты её проекции P′ на плоскость xOу приобретут значения (x, y,0) . Поскольку расстояние r = OP′ и угол ϕ являются полярными координатами точки P′ , то x = rcosϕ, y = rsinϕ.

Рис. 53.1

Учитывая, что OP′ = ρsinθ и z=ρcosθ, получим связь сферических и декартовых координат в виде

Пусть для примера поверхность задана в декартовых координатах уравнением

(x2 + y2 + z2 )2 = a2 (x2 + y2 ).

По такому уравнению представить вид поверхности весьма непросто. Перейдём к сферическим координатам, пользуясь соотношениями (53.1)

= a2 (ρ2 sin2 θcos2 ϕ+ρ2 sin2 θsin2 ϕ).

После очевидных преобразований уравнение упрощается

ρ4 (sin2 θ+ cos2 θ)2 = a2ρ2 sin2 θ ,

что дает ρ2 = a2 sin2 θ или, окончательно, ρ = asinθ .

Теперь можно представить вид поверхности. Во-первых, ясно, что она имеет одинаковые сечения плоскостями ϕ = const . Во-вторых, можно определить вид этих сечений. Для этого перейдём в плоскости yOz к де-

картовым координатам по формулам, которые получаются из (53.1), если

ϕ = π2

z = ρcosθ

y = ρsinθ .

Уравнение сечения рассмотрим в виде ρ2 =aρsinθ, что дает в координатах

Видим, что сечение это является окружностью радиуса a .

2

Пришли к тому, что исходная поверхность представляет собой тор, т.е. закрученную вокруг оси Oz окружность, закрепленную в начале координат (половина поверхности изображена на рисунке 53.2).

91