
10303
.pdfДействительно, в силу чётности функции f (x) площади фигур, выражаемые интегралами
0 |
π |
S1 = ∫ f (x) dx , |
S2 = ∫ f (x) dx , |
− π |
0 |
π |
|
равны, поэтому S = ∫ f (x) dx = S1 + S2 . Также и коэффициентыan вычис-
−π
ляются по формулам
a = |
1 |
π |
f (x)cos nx dx = |
2 |
π |
f (x)cos nx dx. |
p |
|
|||||
n |
−∫π |
|
p ∫0 |
|
||
|
|
|
|
|
|
|
Последнее равенство следует из предыдущих рассуждений, т.к. подынтегральная функция – чётная. Коэффициенты при синусах обращаются в нули, как интегралы от нечетных функций по промежутку, симметричному относительно начала координат.
Итак, если функция четная, то её ряд Фурье имеет вид
|
a0 |
|
|
∞ |
|
|
|
|
|
2 |
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f (x) = |
+ |
∑an cos nx , an = |
|
|
f (x)cos nx dx , n = 0,1,... , bn |
= 0 |
||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
2 |
|
n=1 |
|
|
|
|
|
p ∫0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример. Разложим в ряд Фурье функцию |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
f (x) = x2 , - p £ x £ p, T = 2p. |
|
||||||||||||||||||||||
Вычисляем коэффициенты ряда: |
π x2 dx = |
|
|
|
|
|
π = |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
a0 = |
2 |
|
2 |
× |
x3 |
|
2p2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
p |
p |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
∫0 |
|
|
|
3 |
0 |
|
|
|
|
3 |
|
|
|
|
||||||||
|
|
|
|
|
2 |
π |
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
π |
|
|
2 |
π |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
= |
|
∫ |
x2 cos nx dx = |
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
∫ |
|
|
||||||
|
|
a |
n |
|
|
|
|
x2 |
|
|
sin nx |
|
|
|
|
|
|
x sin nx dx |
||||||||||||
|
|
|
|
p 0 |
|
|
|
|
|
|
p |
n |
|
|
|
|
|
|
|
|
|
n 0 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Интегрируя ещё раз «по частям», получаем:
|
|
|
|
2 |
|
|
2 |
|
|
|
|
1 |
|
|
|
π |
|
1 |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
a |
|
= |
- |
× |
-x |
|
× cos nx |
+ |
∫ |
cos nx dx |
= |
|||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
n |
|
|
|
|
|
n |
|
|
|
n |
|
|
n |
|
|
|
|
||||||
|
|
|
|
p |
|
|
|
|
|
0 |
|
0 |
|
|
|
|
||||||||
|
4 |
|
- p cos pn + |
|
1 |
|
|
π |
= (-1)n |
4 |
|
|
||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
= - |
|
|
sin nx |
|
|
, n =1, 2, K |
||||||||||||||||||
|
|
|
|
n2 |
||||||||||||||||||||
|
pn |
|
n |
|
|
|
n2 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
162 |
|
0 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким образом, x2 = p |
2 |
∞ |
|
|
cos nx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
- 4∑(-1)n+1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
3 |
n=1 |
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Полагая в этом равенстве |
x=0 , |
получаем числовой ряд: |
|
||||||||||||||||||||||||
p |
2 |
|
|
∞ |
|
|
1 |
|
|
1 |
|
|
|
1 |
|
1 |
|
1 |
|
1 |
|
1 |
|
|
|||
= |
∑(-1)n+1 |
=1 - |
|
+ |
- |
+ |
- |
+ |
- ... |
(60.5) |
|||||||||||||||||
|
n2 |
|
|
|
|
|
|
|
|||||||||||||||||||
12 |
|
|
n=1 |
|
|
4 |
|
|
9 16 |
25 |
36 49 |
|
|
||||||||||||||
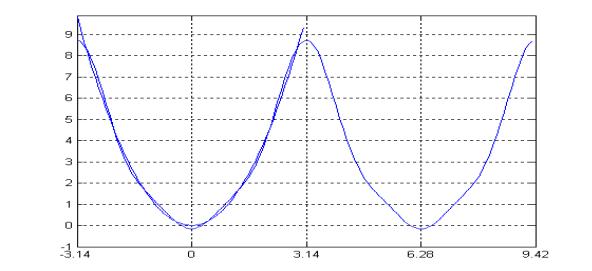
На следующем рисунке представлено приближение функции x2 |
тремя |
||||||||||||||||||||||||||
гармониками |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
p2 |
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
||||||||
|
x |
|
» y3 |
= |
- 4 × cos x - |
|
|
|
cos 2x + |
|
cos3x |
|
|||||||||||||||
|
|
4 |
|
9 |
|
||||||||||||||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Рис.60.7
Скажем несколько слов о влиянии свойств функции на характер сходимости её ряда Фурье. Мы уже отмечали, что около точек разрыва функции ряд Фурье сходится медленнее, чем в точках непрерывности. Гладкость функции, т.е. её дифференциальные свойства также улучшают сходимость ряда. Когда мы разложили в ряд «клюшку» (см. рис. 60.3), то в точке её «излома» при x=0 получили
p2 |
=1 + |
1 |
+ |
1 |
+ |
1 |
+ ... + |
1 |
+ ... |
(60.6) |
8 |
|
|
|
(2k -1)2 |
||||||
9 |
25 |
49 |
|
|
|
|||||
В этой точке функция непрерывна, но не имеет производной. Подсчитаем число π , взяв одинаковое число членов разложения в рядах (60.5) и (60.6) (пусть п = 7). Во-первых, ряд (60.5) дает возможность оценить ошибку, т.к. он знакочередующийся и ошибка при отбрасывании остатка
163
меньше 1/64 ≈ 0,016. Из ряда (60.6) получаем π ≈ 3,06, а ряд (60.5) дает π ≈ 3,16.
Лекция 61. Ряды Фурье (продолжение)
61.1. Разложение в ряд Фурье нечетных функций. Для нечётных функций ряд Фурье имеет вид:
|
|
|
|
|
|
∞ |
|
|
|
|
|
f (x) = ∑bn sin nx , |
|
|
|
|
|
π |
|
n=1 |
где |
b |
= |
2 |
f (x) sin nx dx , a = 0, n = 0,1,... |
||
|
||||||
|
n |
|
p ∫0 |
n |
|
|
|
|
|
|
|
||
Коэффициенты при косинусах обращаются в нули, как интегралы от нечетных функций по промежутку, симметричному относительно начала координат.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1, − π < x < 0, |
||||
Пример. Разложим в ряд Фурье функцию f (x) = |
|
|
|
|
x = 0 |
|||||||||||||||||||||||||
0, |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, |
0 < x < π |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 – |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
׀ |
|
|
|
|
• |
|
|
|
׀ |
|
|
|
׀ |
׀ |
|
|
|
|
x |
||
|
|
|
|
|
|
-π |
|
|
|
|
|
|
|
|
π |
|
|
2π |
3π |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.61. 1 |
|
|
|
|
|
|
|
||||
|
|
π sin nx dx = - |
|
|
|
|
|
|
|
π = |
|
|
|
|
|
|
|
0, |
|
n - четное |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
b = |
2 |
2 |
× |
1 |
cos nx |
2 |
× |
1 |
(1 - cos pn) |
= |
4 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||
n |
p |
∫0 |
|
|
|
|
|
|
p n |
|
|
|
0 p |
|
n |
|
|
|
|
|
, n - нечетное |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
4 |
|
∞ |
sin (2k + 1)x |
|
|
|
|
|
|
pn |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Итак, |
|
f (x) = |
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
||||||||
|
|
|
2k + 1 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
π k =0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
− π 4, |
− π < x < 0, |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
sin x + |
|
|
sin 3x + |
|
|
sin 5x + |
|
sin 7x + ... = |
0, |
x = 0 |
|
|
|
|
||||||||||||||||
|
|
5 |
7 |
|
|
|
|
|||||||||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π 4, |
0 < x < π |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
164 |
|
|
|
|
|
|
|
|
|
|
||||
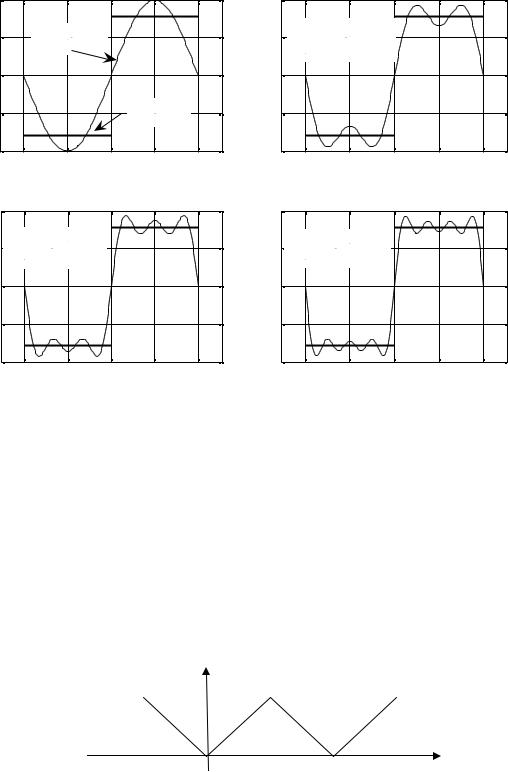
Следующие рисунки показывают, как происходит «приближение» суммы гармоник по мере увеличения их числа к этой кусочно-постоянной функции.
1 |
|
|
|
|
|
1 |
|
|
|
|
|
0.5 |
|
y =sinx |
|
|
|
0.5 |
y2=y1+(1/3)sin3x |
|
|
||
|
|
1 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
−0.5 |
|
|
|
y=-pi/4 |
|
−0.5 |
|
|
|
|
|
−1 |
−π |
−π/2 |
0 |
π/2 |
π |
−1 |
−π |
−π/2 |
0 |
π/2 |
π |
|
|
||||||||||
1 |
|
|
1 |
|
|
|
0.5 |
y3=y2+(1/5)sin5x |
|
0.5 |
y4=y3+(1/7)sin7x |
|
|
0 |
|
|
0 |
|
|
|
−0.5 |
|
|
−0.5 |
|
|
|
−1 |
−π −π/2 0 |
π/2 π |
−1 |
−π −π/2 0 |
π/2 |
π |
|
|
|||||
|
|
|
Рис. 61.2 |
|
|
|
|
61.2. Разложение произвольной функции только по косинусам или |
|||||
только по синусам. |
Если в промежутке [-π, π] функция |
f (x) |
не обладает |
|||
симметрией, т.е. не является ни чётной, ни нечётной, а нужно получить разложение её в ряд Фурье только по косинусам или только по синусам, то
такое разложение можно получить в промежутке |
[0, π ], а на промежуток |
[-π, 0] продолжить её чётным или нечётным образом. |
|
Пример. Разложим в ряд Фурье функцию |
f (x) = x, 0 ≤ x ≤ π . Про- |
должим её чётным образом в промежуток [-π;0], а затем с промежутка [- π;π ]на всю ось с периодомÒ = 2π (см. рис.61.3).
π−
׀׀
−π O |
π |
2π |
x |
Рис.61.3
165
|
|
|
|
|
|
|
|
|
|
2 |
|
π |
|
|
|
2 |
|
x2 |
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Вычисляем коэффициенты: a = |
|
|
∫ |
x dx = |
|
× |
|
|
|
= p |
|
|
|
|||||||||||||
p |
p |
2 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
n |
|
2 |
π |
|
2 x |
|
π |
|
|
1 |
π |
|
|
|
|
|
|
2 |
2 |
|
|
π |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= |
|
∫ |
x cos nx dx = |
|
|
×sin nx |
|
- |
|
|
|
∫ |
|
|
|
|
= |
|
|
|
= |
|||||
a |
|
|
|
|
|
|
|
|
|
|
sin nx dx |
|
|
cos nx |
|
|||||||||||
|
|
p 0 |
|
p n |
|
0 |
|
|
|
n 0 |
|
|
|
|
|
|
pn |
|
|
|
0 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
= |
2 |
(cos pn -1) = |
|
|
|
0, n - четное |
|
|
|
||||||||||||
pn2 |
|
|
pn2 , n - нечетное |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
-4 |
|
|
|
|||||||||||
|
|
|
π |
|
4 |
|
∞ cos |
( |
2k −1 x |
|
|
|
|
|
|
||||||
Таким образом, x = |
− |
|
∑ |
|
|
|
|
|
) |
0 ≤ x ≤ π. |
|
|
|
||||||||
2 |
|
|
|
|
(2k −1) |
2 |
|
|
|
||||||||||||
|
|
|
|
π k=1 |
|
|
|
|
|
|
|
||||||||||
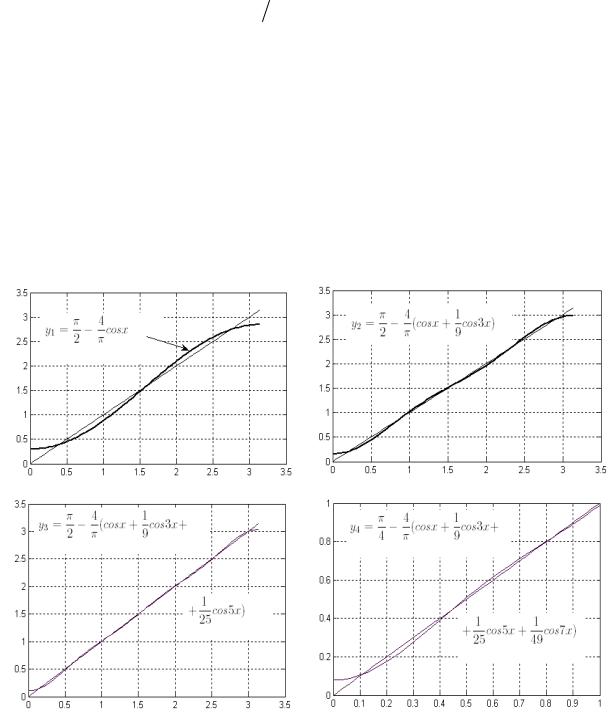
На следующем рисунке |
приведены графики первых членов ряда Фу- |
||||||||||||||||||||
рье (п=5) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x » p - |
4 |
cos x + |
1 |
cos 3x + |
1 |
cos 5x + |
1 |
cos 7x , |
|||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
2 |
|
|
p |
|
|
9 |
|
|
25 |
|
49 |
|
||||||
последовательно приближающих функцию f (x) = x |
в промежутке[0,π]. |
||||||||||||||||||||
Рис. 61.4
166
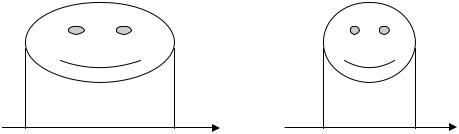
Обратите внимание, что на четвёртом рисунке изображён только фрагмент графика, так как в прежнем масштабе графики были бы неразличимы.
Также ещё раз обращаем внимание на тот факт, что там где «раскладываемая» функция недостаточно «хороша» её аппроксимация отрезками ряда в этих точках «хуже». В нашем случае такая «плохая» точка – начало координат, где функция не имеет производной (см. рис. 61.4)
61.3. Разложение в ряд Фурье функции по произвольному проме-
жутку. Предположим, что некоторую функцию f (x) , определенную в промежутке [a, b], мы хотим представить рядом Фурье. Положение и длина промежутка несущественны, т.к. «сдвигом» и «растяжением» с помощью линейного преобразования
x = |
a + b |
+ |
b − a |
|
|
2π |
|
a + b |
|
|
|
t ; |
t = |
|
× x - |
|
|
||
2 |
2π |
|
|
||||||
|
|
|
|
b - a |
2 |
||||
Промежутокa≤ x ≤ bприводится к стандартному промежутку – π ≤ t ≤ π(см.
рис. 61.5).
|
|
|
|
|
|
t |
|
|
|
|
|
|
x |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−π |
|
|
π |
|
|
|
|
|
|
|
a |
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
Рис. 61.5 |
|
|
|
|
|||||
Пусть функция задана в промежутке [- l, l] и имеет период 2l, т.е. |
|||||||||||||||
|
|
|
f (x + 2l) = f (x) . |
|
|
|
|
|
|
|
|||||
Несложная замена переменной |
x = |
l |
t, |
|
t = π x |
«возвращает» нас к |
|||||||||
|
|||||||||||||||
|
|
|
|
|
|
|
π |
|
|
|
l |
|
|
||
стандартному случаю. |
Функция f ( x) = f |
l |
t |
как функция переменной t |
|||||||||||
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
||
будет иметь периодT = 2π . Действительно, |
|
|
|
|
|||||
f |
l |
(t + 2π) |
= f |
l |
t + 2l = f |
( x + 2l ) = f ( x) = f |
l |
t |
, |
|
|
|
|||||||
π |
|
π |
|
π |
|
|
|||
|
|
|
|
|
167 |
|
|
|
|
т.е., прибавив к аргументу функции число 2π, мы получили то же самое значение функции.
Для функции f ( x) = f |
l |
|
t |
имеем ряд Фурье |
||||
|
||||||||
|
π |
|
∞ |
|||||
f |
l |
t |
|
a0 |
||||
= |
+ ∑an cos nt + bn sin nt , |
|||||||
|
|
|||||||
π |
|
|
2 |
n=1 |
||||
где коэффициенты ряда вычисляются по формулам:
|
1 π |
|
l |
|
|
1 π |
|
l |
|
|
|
|
||||||
an = |
|
−∫π f |
|
|
t |
cos nt dt , bn |
= |
|
−∫π f |
|
|
t |
sin nt dt , |
n = 0,1, 2,K |
||||
π |
π |
π |
π |
|||||||||||||||
«Возвратимся» к старой переменной |
|
x = |
l |
t t = π x , тогда ряд примет |
||||||||||||||
|
π |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
вид |
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
f ( õ ) = |
+ ∑a n cosn πx +b n sinn πx , |
|||||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
2 |
|
n=1 |
|
|
|
l |
|
|
l |
|||
а коэффициенты после этой несложной замены будут вычисляться по формулам:
a = |
1 |
l |
f ( x)cos n π x dx , |
b = |
1 |
l |
f ( x)sin n π x dx, n = 0,1,K |
|
|
||||||
n |
l −∫l |
l |
n |
l −∫l |
l |
||
|
|
||||||
168
Раздел 12. Элементы теории множеств, математической логики и теории графов
Лекция 62. Элементы теории множеств
62.1 Общие представления о множествах. Обычно, когда вводится какое-либо новое понятие, то оно опирается на известное понятие или известные понятия, частным случаем которого или которых оно является. Например, параллелограмм есть четырехугольник, у которого противоположные стороны равны и параллельны. Окружность есть линия на плоскости, все точки которой удалены от некоторой фиксированной точки на некоторое фиксированное расстояние и т.д.
Понятие множества является первичным и не имеет формального определения. Один из создателей теории множеств Георг Кантор(1845-1918) сказал: «Множество есть многое, мыслимое нами как единое». Интуитивно под множеством понимается совокупность различных объектов, объединенных по какому-то одному или нескольким признакам.
Нет никаких ограничений на природу объектов, составляющих множество. Так, про окружность можно сказать, что это множество точек, равноудаленных от фиксированной точки на расстояние радиуса. Можно говорить о множестве студентов в данной аудитории, о множестве букв некоторого алфавита, о множестве целых числа от 1 до 1000, о множестве атомов серебра в данной монете или о множестве всевозможных идей, которые имело человечество, и т.д.
Множества часто обозначают прописными латинскими буквами A, B,C, X ,Y . Объекты, составляющие множество, называются элементами
множества и |
обычно обозначаются строчными латинскими |
буквами |
a, b, c, , x, y . |
Тот факт, что объект x принадлежит множеству A, |
передает- |
ся записью x A(читается – « элемент x принадлежит множеству A»). Если x не является элементом A, то пишут x A.
Два множества A и B считаются равными (записывается A = B), если они состоят из одних и тех же элементов. Т.е. A = B тогда и только тогда, когда из того, что x A следует, что x B , а из того, что x B следует, что x A.
Существует два основных способа задания множеств: перечисление и описание. При первом способе просто перечисляются все элементы задаваемого множества. Например, множество букв алфавита некоторого языка определяется списком всех его букв, множество студентов в группе определяется студентами, фамилия и имена которых совпадают со списком в журнале посещаемости, множество простых чисел меньших тысячи может быть задано перечислением всех таких чисел и т.д. В дальнейшем будем пользоваться общепринятыми обозначениями множеств:
169

N – множество натуральных чисел, Z – множество целых чисел,
Q – множество рациональных чисел,
R – множество действительных чисел,
C – множество комплексных чисел.
Конечно, нельзя ни одно из этих множеств (хотя бы в силу их бесконечности) задать перечислением их элементов. Но опыт работы с элементами этих множеств позволяет предполагать, что в каждой конкретной задаче понятно, об элементах каких из перечисленных множеств идет речь.
При втором способе элементы множества задаются при помощи характеристического свойства, устанавливающего, какие элементы (принадлежащие, как правило, некоторому объемлющему множеству) принадлежат задаваемому множеству. В этом случае в фигурных скобках записывается произвольный элемент множества, а за вертикальной чертой записываются свойства, которыми этот элемент должен обладать:
A = {x P ( x ) }.
Эта запись означает, что Aесть множество таких элементов x , которые обладают свойствами P(x) .
Свойства P(x) могут быть заданы или в виде словесного описания, или в виде неравенств, или в виде уравнений. Например, множество натуральных чисел от 1 до 1000 может быть записано таким образом:
N 1000 = {x x N и x ≤ 1000}.
Множество, записанное следующим образом:
|
|
n N и уравнение xn + yn = zn |
|
Ф= n |
|
имеетрешениевцелыхчислах |
|
|
|
|
|
|
связано с великой теоремой Ферма.
Однако состав множества, определенного описанием, не всегда очевиден, и причина этого кроется гораздо глубже, чем просто недостаточная выразительность языка. Так, только недавно было доказано (доказана теорема), что приведенное выше множество Ф состоит всего из двух эле-
ментов: Ф={1,2}.
Если множество A содержит конечное число элементов, то говорят, что оно конечно, в противном случае множество Aназывается бесконечным. Если множество Aконечное, то A будет означать число элементов в
A. Приведенные множества N1000 и Ф конечные, причем N 1000 = 1000 и
Ф = 2 , а описанные множества пар чисел
170
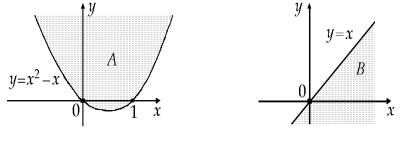
A = {( x, y) |
|
y ³ x 2 - x и |
B = {(x, y) |
|
y ≤ x}, |
|
|
||||
|
|
||||
|
|
|
|
|
|
геометрические инте рпретации которых приведены на рис. 62.1, являются бесконечными.
Рис. 62.1
Само слово «множество» наводит на мысль, что в множестве содержится много элементов. Но это не так. Можно рассматривать множества, состоящие всего из одного элемента, и даже множество, не имеющее ни одного элемента. Последнее множество называется пустым множеством и для него существует о бозначение: . Например, множество
A = {x |
|
x N и для любого натурального числа |
y N, |
что xy = y} |
||
|
||||||
состоит всего из одн ого элемента, которым является 1, |
а множество |
|||||
|
|
B = x |
|
x N и x2 +1= 0 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
не содержит элементо в и, следовательно, B= .
Все пустые множества равны между собой, иначе говоря, существует только одно пустое множество.
62.2. Подмножества. Универсальное множество. Множество всех подмножеств данного множества. Понятие подмножесства возникает тогда, когда необходим о рассматривать некоторое множество не самостоятельно, а как часть дрругого, более широкого множества. Множество B называется подмножеством множества A (записывается
элемент множества B является элементом множества A . Запись B A не исключает, что
Пустое множество является подмножеством любого множества. Из определения следует, что любое множество является подмножеством самого себя: A A . Таким образом, у каждого множества (кроме пустого) есть, по крайней мерее, два подмножества – само множество и пустое множество. Нетрудно проверить следующее свойство: из того, что A B, а B C следует, что A C . В самом деле, будем рассуждать от противного. Пусть A B и B C , но A Ë Cи A ¹ C . Тогда существует такой элемент,
171
