
10298
.pdf

Таким образом, правая часть в (29.1) является первообразной подынтегрального выражения слева.
Применение этой формулы позволяет находить интегралы сложных функций, используя таблицу основных интегралов. Например, найдем
cos(3x 2)dx .
Зная, что
cosudu sin u C
иделая в этойформулеподстановкуu 3x 2 , получим
cos(3x 2)d (3x 2) sin(3x 2) C ,
откуда найдем
cos(3x 2)dx 13 sin(3x 2) C .
Этот прием, основанный на подстановке некоторой функции в готовую формулу табличного интеграла, называют методом подстановки.
Рассмотрим теперь приём интегрирования с помощью замены переменной. Предположим, что нужно найти интеграл f (x)dx . Заменяем переменную интегрирования некоторой дифференцируемой функцией x (t) , имеющей обратную функцию t (x) . Предположим также, что (t) не-
прерывна.Тогда справедлива формула замены переменной в неопреде-
ленном интеграле
|
(29.2) |
f (x)dx f ( (t)) (t)dt , t (x) . |
|
Действительно, пусть F (x) первообразная |
f (x) . Тогда по формуле |
подстановки правая часть этого выражения равна |
|
f ( (t)) (t)dt F( (t)) C F(x) C
при x (t) , что подтверждает справедливость формулы (29.2).
Прием замены переменной состоит в том, чтобы после её проведения сделать такую замену, при которой для подынтегральной функции в полученном интеграле справа в (29.2) легко может быть найдена первообразная.
Например, для нахождения интеграла 
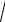 a2 x2 dx сделаем замену переменной x a sin t так, что
a2 x2 dx сделаем замену переменной x a sin t так, что
211
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
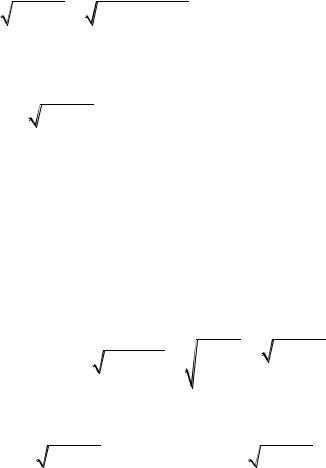
a2 x2 |
|
|
|
|
a2 a2 sin2 t a cost |
, dx a cost dt . |
||||||||||||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 cos 2t |
|
|
a |
2 |
x |
2 |
dx |
a |
2 |
cos |
2 |
tdt |
a |
2 |
|
dt |
|||||||
|
|
|
|
|
|
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
1 |
|
|
|
|
|
|
a2 |
t sin t cost C . |
||||||||
|
|
|
|
|
t |
|
|
|
sin 2t |
|
C |
|
|||||||||
|
2 |
|
2 |
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Перейдём от переменной t к переменной x . В промежутке a x a
существует обратная функция t arcsin |
x |
|
, поэтому |
|
|
||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
1 |
x2 |
|
|
|
|
a2 x2 |
. |
|||||||
cost 1 sin2 t |
|
||||||||||||||||||||
a2 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|||||
Окончательно получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
dx |
a2 |
arcsin |
x |
|
x |
|
|
|
|||||||||||
a2 x2 |
|
a2 x2 |
C . |
||||||||||||||||||
|
|
|
|
||||||||||||||||||
2 |
|
|
|
|
|
a |
2 |
|
|
|
|
|
|||||||||
Заметим в заключение этой темы, что в некоторых случаях замену переменной непосредственно не осуществляют, а применяют так называемую операцию «внесения под дифференциал». Заменяя выражение (x)dx диф-
ференциалом d (x) , получают
f ( (x))d (x) f ( )d .
Например, |
|
|
|
||||
|
1 |
|
1 |
|
3x 7 |
11 |
|
3x 7 10dx |
3x 7 10 d 3x 7 |
|
|
|
C . |
||
3 |
3 |
11 |
|
||||
212

Лекция 30. Методы интегрирования (продолжение)
30.1.Интегрирование простейших иррациональностей.Рассмотрим только простейшие случаи иррациональных подынтегральных функций.
Если интеграл содержит иррациональность вида n ax b a 0 , то приме-
ax b a 0 , то приме-
няют подстановку |
ax b tn . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
Пример.Найти интеграл |
|
|
1 |
|
dx . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Сделаем замену или x t2 . Тогда |
dx 2tdt и |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
dx |
2t dt |
2 |
t 1 1 |
dt |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x 1 |
|
|
|
|
t 1 |
|
|
|
t 1 |
|
|
||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
2 t |
|
|
|
dt 2 t |
ln |
t 1 |
C = 2( x ln |
|
|
x 1) C . |
||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
t 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Если |
подынтегральное |
выражение |
содержит иррациональностивида |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ax b t p с p , |
||||||||||||||||||||
n ax b и |
m ax b , |
где |
|
|
|
m n , то применяют подстановку |
|||||||||||||||||||||||||||||
равным наименьшему общему кратному чисел m и n . |
|
|
|||||||||||||||||||||||||||||||||
|
Рассмотрим интегралы вида |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
Mx N dx |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
. |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
Ax2 Bx C |
|
|
Ax2 Bx C |
|
|
||||||||||||||||||||
Первый из них сводится к табличному интегралу выделением полного квадрата в подкоренном выражении. Для нахождения второго интеграла следует в числителе выделить дифференциал квадратного трехчлена d ( Ax2 Bx C) (2Ax B)dx .
213
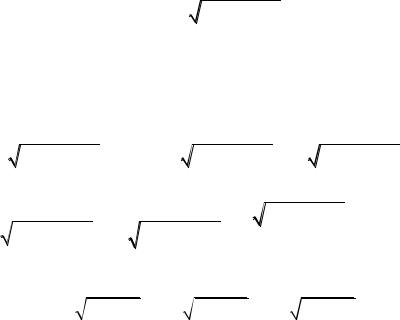
Пример. Найтиинтеграл I |
|
x 2 dx |
|
|
|
. |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
3 2x x |
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
В числителе |
|
дроби получим |
дифференциал подкоренного |
выражения |
|||||||||||||||||||||||||||||
d (3 2x x2 ) (2 2x)dx и разобьём интеграл на два интеграла |
|
|
|
||||||||||||||||||||||||||||||
I |
1 |
|
|
(2 2x) 2 |
|
dx |
1 |
|
|
(2 2x)dx |
|
|
|
dx |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
3 2x x2 |
3 2x x2 |
3 2x x2 |
|
||||||||||||||||||||||||||||||
1 |
|
|
d (3 2x x2 ) |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
3 2x x2 arcsin |
C |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||||||||||||||
|
|
|
3 2x x2 |
|
4 (x 1)2 |
|
|||||||||||||||||||||||||||
Винтегралах вида

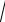 a2 x2 dx ,
a2 x2 dx , 
 a2 x2 dx ,
a2 x2 dx , 
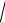 x2 a2 dx
x2 a2 dx
освобождаются от иррациональности применением тригонометрических подстановок. Для первого интеграла применяется замена x a sin t (можно
x acost ) и используется тождество |
sin2 t cos2 t |
1; для второго – за- |
||||||
мена x a tgt |
и применяется соотношение 1 tg2 t |
1 |
; для третьего – |
|||||
|
cos2 t |
|||||||
|
|
|
|
|
|
|
|
|
замена x |
a |
или x |
a |
. |
|
|
|
|
cos t |
sin t |
|
|
|
|
|||
|
|
|
|
|
|
|
||
30.2. Интегрирование по частям.Рассмотрим метод интегрирования, который позволит нахождение одного интеграла заменить отысканием другого, «более простого». В основу этого метода положено следующее рассуждение. Пусть u (x) и v(x) – две функции, имеющие непрерывные произ-
водные на некотором интервале. Найдем дифференциал d (u v) от произведения этих функций
d (u v) u dv v du ,
где dv v (x) dx, du u (x) dx . Перепишем это выражение в виде u(x) dv(x) d (u(x) v(x)) v(x)du(x)
и проинтегрируем обе его части. Учитывая, что d (u v) u v , получим
формулу интегрирования по частям
u(x) dv(x) u(x) v(x) v(x) du(x) .
214

Метод интегрирования по частям состоит в представлении интеграла
f (x)dx
ввиде u(x) dv(x) так, чтобы интеграл v(x) du(x) в правой части формулы
интегрирования по частям оказался «более простым». При нахождении функции v(x) можно произвольную постоянную C , возникающую при этом
интегрировании, положить равной нулю.
Найдем интеграл x e xdx . Введем обозначения: u(x) x , dv(x) e xdx . Тогда du(x) dx и v(x) e xd ( x) e x .
Применяя формулу интегрирования по частям, получим
x e xdx x e x e xdx x e x e x C .
Формула интегрирования по частям предполагает разбиение подынтегрального выражения на два множителя u(x) и dv(x) , причем при переходе
к правой части первый дифференцируется, а второй интегрируется. Нужно стараться, во-первых, чтобы интегрирование дифференциала dv не пред-
ставляло трудностей и, во-вторых, чтобы интеграл v(x) du(x) имел более
простое подынтегральное выражение. Так, в предыдущем примере было бы «неразумно» положить u e x , а dv xdx . Действительно, в этом случае
x e xdx x2 e x 1 x2 e xdx ,
2 2
мы получили более сложный интеграл, чем первоначально данный. Заметим, что если мы имеем интегралы вида
Pn (x)sin kxdx , Pn (x)cos kxdx , Pn (x)ekxdx ,
( Pn x – многочлен n -ой степени), то следует выбрать u(x) Pn (x) . При
этом интегрирование по частям проводится столько раз, какова степень многочлена Pn (x) . Если же имеем интегралы вида
Pn (x)arcsin kx dx , Pn (x)arccos kx dx , Pn (x)arctg kx dx ,
215

Pn (x)arcctg kx dx , Pn (x)loga kx dx ,
то выбираем в качестве функции u(x) либо обратную тригонометрическую функцию, либо логарифм.
30.3. Интегрирование выражений, содержащих тригонометриче-
ские функции.Разнообразие тригонометрических функций и особенно формул, их связывающих, приводит к большому выбору методов вычисления интегралов, содержащих тригонометрические функции. Рассмотрим некоторые из этих методов интегрирования.
Для нахождения интегралов вида sin x cos x dx , sin xsin x dx ,
cos x cos x dx , где , – действительные числа, следует преобразовать произведения тригонометрических функций в суммы по формулам
sin x cos x 12 sin x sin x , sin x sin x 12 cos x cos x , cos x cos x 12 cos x cos x .
Пример.Найти интеграл |
I sin 3x cos7x dx . |
||||||
I |
1 |
sin 4xdx sin10xdx |
1 |
cos 4x |
1 |
cos10x C . |
|
|
|
|
|||||
2 |
8 |
20 |
|||||
Рассмотрим несколько случаев нахождения интегралов вида
sin x cos x dx
взависимости от различных значений чисел и .Если хотя бы одно из чисел или –положительное целоенечетноечисло, то поступают следу-
ющим образом: отделяют от тригонометрической функции в нечетной степенифункцию в первой степени и вносят ее под знак дифференциала. Оставшуюся четную степень тригонометрической функции преобразуют с использованием формулы sin2 x cos2 x 1.
Пример. Найти интеграл |
|
sin3 |
x |
|
dx . |
||
|
|
|
|
|
|||
3 cos2 x |
|||||||
|
|
|
|||||
|
216 |
|
|
||||


|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 t |
|
|
dt |
1 |
|
d 2t |
|
1 |
1 2t |
|
|
1 |
1 2 tg x |
|
|||||||||
I |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
С |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |
|
|
|
|
ln |
|
|
|
||||
|
5 |
t2 |
|
1 4t2 |
2 |
1 2t 2 |
4 |
1 2t |
4 |
1 2 tg x |
|||||||||||||||
1 |
1 t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Интеграл вида R sin x,cos x dx , |
где R(sin x,cos x) – рациональная |
||||||||||||||||||||||||
функция синуса и косинуса, можно привести к интегралу рациональной дроби (правильной или неправильной)с помощью универсальной тригоно-
метрической подстановки
t tg 2x , x .
В этом случае sin x и cos x выражаются по известным тригонометрическим формулам через новую переменную t следующим образом:
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
|
2t |
|
, cos x |
1 t2 |
, |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t2 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 t2 |
|
|
|
|
|
|
|
||||||||||
а из соотношения |
t tg |
x |
|
следует, |
что |
|
x |
arctg t |
и |
dx |
|
2dt |
. |
|
||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 t2 |
|
|
|||||||
Пример.Найти интеграл I |
|
|
|
|
|
|
|
dx |
|
. |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
4cos x 3sin x 5 |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Применяя универсальную подстановку |
t tg |
x |
, |
|
получаем |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
2dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
2 |
|
|
|
|
|
2 |
|
|
|||||||||||
I |
|
|
|
1 t2 |
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
= |
|
|
C |
|
|
|
|
C . |
||||||||||||||||||
|
|
1 t2 |
|
|
2t |
|
t 3 2 |
t 3 |
|
x |
|
|||||||||||||||||||||||
4 |
|
|
3 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg |
|
|
3 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
1 t2 |
1 t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||||
Заметим, что применение универсальной подстановки часто приводит к достаточно громоздким выражениям, поэтому использовать ее нужно только после того, как исчерпаны другие возможности.
218
Лекция 31. Комплексные числа
31.1. Введение.Вспомним, как развивалось понятие числа, начиная от чисел натуральных до чисел действительных. Если операция сложения во множестве натуральных чисел выполнима без ограничений, то операция обратная сложению, т.е. решение уравнения a x b , выполнима только при b a . Если отказаться от этого ограничения, то получатся «новые» числа – отрицательные. Так «родились» целые числа, во множестве которых сохранены все свойства суммы и обратная операция – разность, результатом которой является число x b a .
Во множестве натуральных чисел также не всегда разрешима задача,
обратная операции умножения, т.е. решение уравнения |
a x b . Для её ре- |
шения необходимо и достаточно, чтобы b было кратно |
a . Возникла необ- |
ходимость расширения множества целых чисел до чисел рациональных. В этом множестве обратная операция – деление, результатом которой является число x b : a , разрешима с ограничением a 0 . Для рациональных чисел сохраняются свойства операций сложения и умножения.
Оказалось, что во множестве рациональных чисел не всегда разрешима задача извлечения квадратного корня из положительного числа,
например, неразрешимо уравнение x2 2 0 . Число 
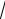 2 , которым мы привычно обозначаем один из корней этого уравнения, число – иррациональное. Это число «должно» бы выражать длину диагонали квадрата со стороной равной единице. Но среди известных чисел, с помощью которых можно выразить длину диагонали, такого числа не нашлось. Такие числа назвали иррациональными, т.е. невыразимыми. Это открытие было сделано во времена Пифагора (580–500 г. до н.э.). Позднее, примерно через 1000 лет, латинские слова рациональный и иррациональный стали связывать со словом рацио – разум. В средневековой математической культуре возник новый термин вместо «иррациональный» – surdus (глухой или немой), т.е. такое число, когда немой его не может высказать другому, а второй (глухой) не может выслушать первого. Сопротивление «разума» исчезло, когда стали интерпретировать иррациональные числа бесконечными десятичными непериодическими дробями.
2 , которым мы привычно обозначаем один из корней этого уравнения, число – иррациональное. Это число «должно» бы выражать длину диагонали квадрата со стороной равной единице. Но среди известных чисел, с помощью которых можно выразить длину диагонали, такого числа не нашлось. Такие числа назвали иррациональными, т.е. невыразимыми. Это открытие было сделано во времена Пифагора (580–500 г. до н.э.). Позднее, примерно через 1000 лет, латинские слова рациональный и иррациональный стали связывать со словом рацио – разум. В средневековой математической культуре возник новый термин вместо «иррациональный» – surdus (глухой или немой), т.е. такое число, когда немой его не может высказать другому, а второй (глухой) не может выслушать первого. Сопротивление «разума» исчезло, когда стали интерпретировать иррациональные числа бесконечными десятичными непериодическими дробями.
Комплексные числа, о которых пойдет речь, возникли из необходимости извлечения квадратного корня из отрицательного числа.Определим «но-
вое» число –«мнимую единицу» i , квадрат которого равен 1, т.е. i 2 1. Расширим множество действительных чисел, вводя числа вида z x iy ,
219
