
9744
.pdfТаким образом, формула (3.8) позволяет находить угол между двумя прямыми на плоскости.
Пример. Найти угол между прямыми l1 : x − 2 y + 1 = 0 и l2 : 3x + y − 3 = 0 .
Решение. Запишем общее уравнение заданных прямых l1 и l2 в виде уравнений с угловыми коэффициентами k1 и k2 ,
соответственно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
l : 2 y = x + 1 или l : y = |
1 |
x + |
1 |
, значит k = |
1 |
; |
|||||||||||||||
|
|
|
|||||||||||||||||||
1 |
|
|
|
|
|
|
1 |
|
|
2 |
2 |
|
1 |
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
l2 : y = −3x + 3 , значит k2 |
= −3. |
|
|
|
|
|
|
||||||||||||||
Подставляя найденные значения k |
= |
1 |
и k |
|
= −3 в формулу |
||||||||||||||||
|
2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(3.8), находим угол ϕ между прямыми l1 |
и l2 : |
|
|
|
|||||||||||||||||
|
- 3 - |
1 |
|
- |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
tgϕ = |
|
2 |
|
= |
2 |
|
= 7 , откуда ϕ = arctg 7 . |
||||||||||||||
|
|
|
|
||||||||||||||||||
|
1 + |
1 |
× (- 3) |
- |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответ: ϕ = arctg 7 .
Заметим, что если требуется вычислить острый угол между прямыми, то правая часть формулы (3.8) берется по модулю, то
есть
|
tgϕ = |
|
k2 - k1 |
|
|
. |
|
|
|
1 + k × k |
2 |
|
|||
|
|
|
|
1 |
|
|
|
Если прямые l1 : y = k1 x + b1 ; |
l2 : y = k2 x + b2 параллельны, то |
||||||
ϕ = 0 и tgϕ = 0 , следовательно, |
из формулы (3.8) получаем, что |
||||||
k2 − k1 |
= 0, то есть k2 = k1 . И обратно, если прямые l1 и l2 таковы, |
||||||
что k1 |
= k2 , значит tgϕ = 0 , то есть прямые параллельны. |
||||||
|
30 |
|
|
|
|||

Если |
прямые |
l и |
l |
2 |
перпендикулярны (ϕ = π ), то |
|||
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
ctgϕ = |
1 + k1 × k2 |
= 0 , |
откуда |
k × k |
|
= -1. Справедливо и обратное |
||
|
2 |
|||||||
|
k2 |
− k1 |
|
1 |
|
|||
|
|
|
|
|
|
|||
утверждение.
Пример. Составить уравнение прямой l , проходящей через точку M (1; 2) и перпендикулярной прямой L : 3x + 2 y − 5 = 0 .
Решение. Перепишем общее уравнение прямой L в виде
уравнения прямой с угловым коэффициентом kL :
L : 3x + 2 y − 5 = 0 ,
L : 2 y = −3x + 5 ,
L : y = − 3 x + 5 , значит k |
|
= − |
3 |
. |
|
|
|
|
|
|
|||||
L |
|
|
|
|
|
|
|
||||||||
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||
Прямые l и L перпендикулярны по условию, значит |
|||||||||||||||
kl × kL = -1, следовательно, kl = − |
1 |
= |
2 |
. |
|
|
|
|
|||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
kL |
|
3 |
|
|
|
|
|
|
|||
Подставляя в уравнение (3.5) k |
|
= |
|
2 |
, x = 1, |
y |
|
= 2 находим |
|||||||
l |
|
|
0 |
||||||||||||
|
|
|
|
|
|
|
|
|
3 |
0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
искомое уравнение прямой l :
l : y − 2 = 2 (x −1) 3
l : 3y − 6 = 2x − 2 l : 2x − 3y + 4 = 0
Ответ: 2x − 3y + 4 = 0.
31
§ 4. Плоскость
Переходим далее к аналитической геометрии в пространстве. Объектом изучения теперь будет плоскость. Если в трехмерном пространстве задана прямоугольная декартова система координат, то положение любой точки однозначно определяется тремя числами - её координатами. Найдем уравнение, связывающее координаты любой точки,
принадлежащей плоскости. Способ получения уравнения плоскости аналогичен выводу общего уравнения прямой на плоскости.
|
Общее уравнение плоскости |
|
|||
Пусть в |
прямоугольной |
декартовой системе |
координат |
||
|
M 0 ( x0 ; y0; z0 ) и |
вектор |
|
{A; B;C} . |
|
задана точка |
N |
Требуется |
|||
составить уравнение плоскости, |
проходящей через точку M 0 и |
||||
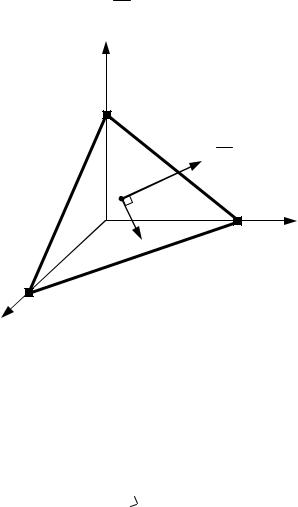
перпендикулярной вектору N (рис. 4.1).
z
N = (A; B;C )
M 0
0 |
M |
y |
|
||
|
|
x
Рис. 4.1
32
Выберем произвольную точку M ( x; y; z) на плоскости.
Тогда вектор M 0M = {x - x0; y - y0 ; z - z0} лежит на плоскости. Так
как плоскость перпендикулярна вектору |
N по условию, то и |
||||||||
|
|
|
|
|
|
|
|
, а значит скалярное |
|
вектор M 0 M перпендикулярен вектору |
N |
||||||||
произведение |
|
× |
|
= 0 , или в координатах |
|
||||
M 0 M |
N |
|
|||||||
|
A ×(x - x0 ) + B ×( y - y0 ) + C ×(z - z0 ) = 0 . |
(4.1) |
|||||||
Уравнение (4.1) является уравнением |
плоскости, |
||||||||
проходящей через точку M 0 (x0 ; y0; z0 ) и перпендикулярной вектору N {A; B;C} .
Вектор N { A; B;C} называется вектором нормали плоскости.
Пример. Составить уравнение плоскости, проходящей через точку M 0 (1;2;3) и перпендикулярной вектору PQ , если P( 0;1;7)
и Q(-1;2;5).
Решение. Находим координаты вектора PQ , являющегося вектором нормали плоскости: N = PQ = {−1;1;−2} .
Подставляя в уравнение (4.1) координаты точки M 0 (1;2;3) и
найденные координаты вектора N , находим искомое уравнение плоскости:
-1×( x -1) +1×( y - 2) - 2 ×( z - 3) = 0 или
−x + y − 2z + 5 = 0
Ответ: −x + y − 2z + 5 = 0 .
Далее преобразуем уравнение (4.1):
Ax − Ax0 + By − By0 + Cz − Cz0 = 0 или
Ax + By + Cz + (− Ax0 − By0 − Cz0 ) = 0 .
33
Обозначив D = −Ax0 − By0 − Cz0 , получаем общее уравнение
плоскости вида |
|
Ax + By + Cz + D = 0. |
(4.2) |
Исследуем уравнение (4.2)
1. При A ¹ 0 , B ¹ 0 , C ¹ 0 , D ¹ 0 уравнение (4.2) примет
вид
Ax + By + Cz = −D .
Разделив обе части последнего уравнения на (−D)
|
|
|
x |
+ |
|
y |
|
+ |
y |
|
= 1, |
||||||
|
|
− D |
− D |
|
− D |
|
|||||||||||
|
|
|
|
A |
|
|
|
|
B |
|
C |
|
|||||
и обозначив |
a = − D |
, b = − D |
B |
, c = − D |
C |
, получаем уравнение |
|||||||||||
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
||||
плоскости «в отрезках»: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
x |
+ |
y |
+ |
z |
= 1, |
|
|
(4.3) |
|||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
a |
|
b |
c |
|
|
|
|
|
|
||||
где a , b и c - величины отрезков, которые плоскость отсекает от осей координат (рис. 4.2).
z
 − CD
− CD
N = (A; B;C )
|
− D |
|
0 |
B |
|
y |
||
|
− D |
A |
x |
Рис. 4.2
34

Пример. Составить уравнение плоскости, проходящей через точку M 0 ( 1;2;3) и отсекающей от осей координат равные
отрезки.
Решение. Используем уравнение (4.3). Так как a = b = c по условию, то его можно переписать в виде x + y + z = a .
Поскольку точка M 0 ( 1;2;3) лежит на плоскости, то,
подставляя ее координаты в последнее уравнение, находим a = 6 .
Следовательно, |
x + y + z = 6 – уравнение искомой плоскости. |
|||||||||||||||
Ответ: x + y + z = 6 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример. Построить плоскость |
6x − 2y + 3z −12 = 0 . |
|||||||||||||||
Решение. Приведем заданное уравнение к уравнению вида |
||||||||||||||||
(4.3): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6x |
− |
2 y |
+ |
3z |
=1; |
|
x |
|
+ |
|
y |
+ |
z |
=1. |
|
|
|
|
|
2 |
|
|
|
|||||||||
|
12 12 |
|
12 |
|
|
|
|
−6 |
4 |
|
||||||
Отметим на оси Ox точку x = 2 , |
на оси Oy точку y = −6, на |
|||||||||||||||
оси Oz точку |
z = 4 , и |
|
через |
эти |
точки |
|
проведем искомую |
|||||||||
плоскость (рис. 4.3).
z
4
− 6 |
0 |
y |

 2
2
x
Рис. 4.3
35
2. Рассмотрим случай, когда в уравнении (4.2) коэффициент
A = 0 . |
|
|
|
|
|
|
|
|
|
|
uur |
|
|
||
Тогда |
вектор |
нормали |
N = 0; B;C оказывается |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{ |
} |
перпендикулярен |
оси |
Ox , |
а плоскость By + Cz + D = 0 , тем |
||||||||||||
самым, - |
параллельна |
|
этой оси. Аналогично – |
при нулевых |
|||||||||||
коэффициентах B или |
C (рис.4.4). |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.4
36
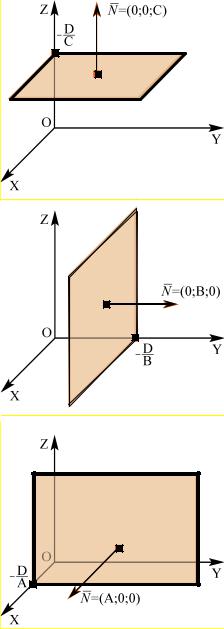
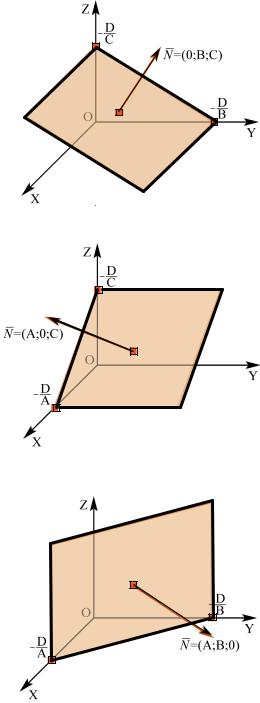
3. Если равны нулю два |
коэффициента перед переменными |
уравнения (4.2), например, |
A = B = 0 , то вектор нормали |
uuur
N = {0;0;C}перпендикулярен координатной плоскости xOy , а
сама плоскость Cz + D = 0 – параллельна ей. Аналогично – при двух других нулевых коэффициентах перед переменными (рис. 4.5).
Рис. 4.5
37

4. Если в уравнении (4.2) D = 0 , то оно задаёт плоскость,
проходящую через начало координат. Для её построения достаточно рассмотреть прямые, которые получаются при пересечении плоскости с координатными плоскостями (рис. 4.6).
Рис. 4.6
5. Допустим, что нулевыми оказываются коэффициент при
одной из |
переменных и свободный коэффициент. Например, |
A = D = 0. |
В этом случае уравнение (4.2) приобретает вид |
By + Cz = 0 и задаёт плоскость, проходящую через ось Ox . Для её построения достаточно добавить ещё одну прямую – например, линию пересечения плоскости с координатной плоскостью yOz (рис. 4.7). При B = D = 0 или C = D = 0
ситуации аналогичны (рис. 4.8).
Рис. 4.7
38

Рис. 4.8
Итак, мы рассмотрели все возможные случаи общего
уравнения (4.2) плоскости.
Уравнение плоскости,
проходящей через три заданные точки
Выведем теперь уравнение плоскости, проходящей через три заданные точки M1 ( x1; y1; z1 ) , M2 (x2; y2; z2 ) и M3 (x3; y3; z3 )
в прямоугольной декартовой системе координат. Для этого рассмотрим произвольную точку плоскости M ( x; y; z) . Три
вектора M1M , M1M 2 и M1M3 компланарны (рис. 4.9),
поэтому их смешанное произведение равно нулю.
39
