
9480
.pdf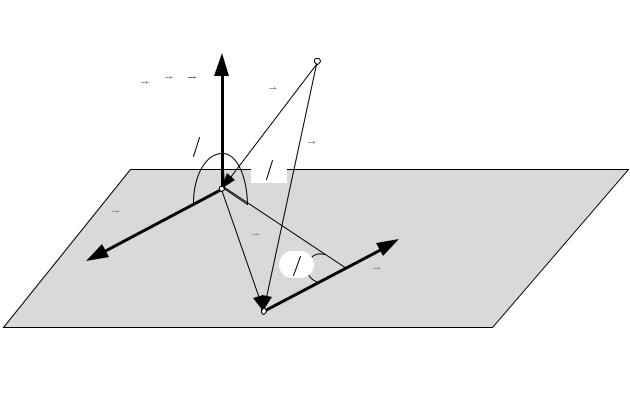
49
произвольной точки пространства О (рис. 6.4). |
|
|
|
|
||||||||||
Преобразуем ее, введя обозначения |
|
|
|
|
|
|
||||||||
= , |
= , |
= ,, и |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
используя определение момента силы и условие = − ′. |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
( ) + |
|
( ′) = |
× + |
× |
|
= × − × = |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− ) × = × |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полученный вектор действительно не зависит от выбора точки О. Видно, что этот вектор направлен так же, как и момент пары, а по
величине равен модулю момента пары :
|
|
|
′ |
) |
| × | = = = (, |
||||
|
|
|
O |
|
m F1, F2 |
r |
|
|
|
|
B |
|
|
|
2 |
|
rA |
|
|
|
2 |
|
|
|
F |
B |
h |
|
|
|
r |
|
|
|
|
|
|
|
|
|
2 |
|
F |
|
|
|
|
|
|
|
A |
|
|
|
|
|
Рис. 6.4 |
||
Таким образом |
|
|
|
|
|
|
|
′ |
) |
|
( ) + |
( ′) = ( , |
||
|
|
|
|
|
СЛЕДСТВИЕ
Если в качестве центра О последовательно выбрать можно получить, что
′ |
|
|
|
|
|
|
( , |
) = |
( ) + |
( ′) = |
( ′), |
||
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
( , |
) = |
( ) + |
( ′) = |
( ). |
||
|
|
|
|
|
|
|
то есть
(6.2)
точку А или В, то
50
момент пары сил равен моменту одной из сил пары относительно точки, в которой приложена другая сила пары.
6.4. ТЕОРЕМА ОБ ЭКВИВАЛЕНТНОСТИ ПАР
ТЕОРЕМА
Две пары, имеющие векторно-равные моменты, эквивалентны друг другу.
Справедливость этой теоремы равносильна справедливости следующих трех утверждений (трех более простых теорем), которые приводим без доказательств.
1.Можно сделать любыми величины сил и плеча пары, сохраняя их произведение, то есть модуль момента пары.
2.Пару можно переносить в любое другое положение в плоскости ее действия и поворачивать ее на произвольный угол.
3.Пару можно переносить на параллельную плоскость действия.
ВЫВОДЫ:
Ни величина силы, ни размер плеча, ни направление сил пары значения не имеют. Существенной характеристикой пары является только ее момент.
Момент пары — вектор свободный. Он не связан с какой-либо точкой пространства или линией действия и может быть перенесен в любую точку тела.
6.5. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИСТЕМЫ ПАР
Рассмотри систему n пар ( , ′ ), где i=1,2,…n произвольно расположенных в пространстве (рис. 6.5).
Момент i-ой пары ( , ′ ) для краткости будем обозначать .
То есть = ( , ′ ).
ОПРЕДЕЛИМ ГЛАВНЫЙ ВЕКТОР СИСТЕМЫ ПАР, для чего просуммируем все силы,
входящие в систему:
= ∑=1( + ′ ).
Поскольку силы пары равны и противоположно направлены, то

51
векторная сумма сил пары будет равна нулю, поскольку = −′ . По этой причине результатом суммирования сил всех пар будет ноль:
= 0.
ОПРЕДЕЛИМ ГЛАВНЫЙ МОМЕНТ СИСТЕМЫ ПАР относительно некоторого центра О,
для чего просуммируем моменты всех сил, входящих в систему:
|
= ∑ |
|
|
|
|
|
|
|
=1 |
( ( ) + |
(′ )) |
||||
|
|
|
|
|
|
|
|
В соответствии с теоремой из §6.3, сумма моментов сил пары относительно любой точки пространства равна моменту пары. Отсюда следует, что
|
= ∑ |
|
|
|
|
) = ∑ |
|
. |
(6.3) |
|
=1 |
( |
, ′ |
=1 |
|||||
|
|
|
|
|
|
|
|
||
m1 |
mi m Fi , Fi |
Fi
i я пара
Fi
mn
Рис. 6.5
Таким образом, мы убедились, что справедлива
ТЕОРЕМА О СЛОЖЕНИИ ПАР
Система пар сил эквивалентна одной результирующей паре, момент которой равен векторной сумме моментов этих пар.
СЛЕДСТВИЯ ИЗ ТЕОРЕМЫ
Моменты двух пар складываются аналогично тому, как складываются силы: по правилу параллелограмма или с помощью треугольника моментов.
52
Для нескольких пар сложение выполняется по правилу многоугольника моментов, которое аналогично правилу силового многоугольника. Результирующая пара будет замыкающей стороной многоугольника моментов. Выполнить построение многоугольника моментов обычно невозможно, поскольку он практически всегда не лежит в одной плоскости. По этой причине его нельзя использовать для графического решения задач.
Поскольку моменты пар не зависят от выбора точки приведения, то и главный момент, как их сумма, в данном случае от выбора центра не зависит.
6.6. УСЛОВИЕ УРАВНОВЕШЕННОСТИ СИСТЕМЫ ПАР
Пара сил не является уравновешенной системой сил. Поэтому для уравновешенности системы пар требуется, чтобы момент результирующей пары был равен нулю. То есть,
для того чтобы система пар была уравновешенной, необходимо и достаточно, чтобы выполнялись следующие условия:
1. В векторной форме:
векторная сумма моментов всех пар должна быть равна нулю:
∑ |
= 0. |
(6.4) |
=1 |
|
|
2.В геометрической форме:
многоугольник моментов пар должен быть замкнут.
3.В аналитической форме:
сумма проекций моментов пар на каждую из координатных осей должна быть равна нулю:
mix 0, |
|
|
|
|
|
miy |
0, |
(6.5) |
|
|
|
miz |
0. |
|
6.7. МОМЕНТЫ ПАР, РАСПОЛОЖЕННЫХ В ОДНОЙ ПЛОСКОСТИ
Если пары расположены в одной плоскости (рис.6.6), то их вектормоменты направлены перпендикулярно к этой плоскости.
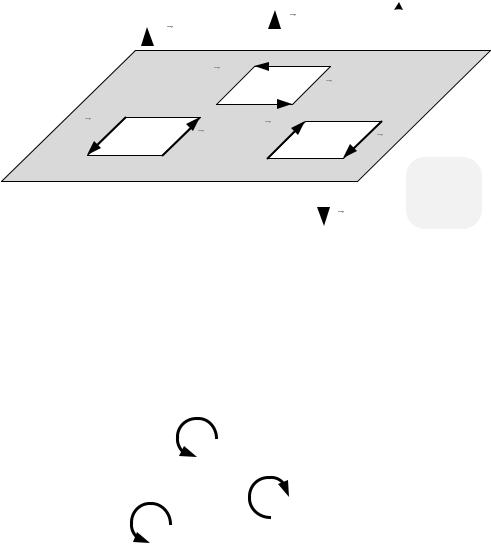
53
В этом случае моменты пар отличаются только модулем и знаком проекции на ось z, перпендикулярную к плоскости действия пар, и могут рассматриваться как скалярные величины.
Проекции эти положительны, если при взгляде на плоскость со стороны положительного направления оси, мы видим пары действующими против часовой стрелки (рис. 6.6).
Для плоской системы сил введем понятие алгебраического момента пары: алгебраическим моментом пары называется взятое со знаком
«плюс» или «минус» произведение одной из сил пары на плечо пары:
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
= ( |
, ′ ) = ± |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
m1 |
|
|
|
|
|
|
m2 |
|
|
|
|
ось z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
F2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
h |
F |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||
|
|
|
|
h1 |
|
|
|
|
|
|
|
2 |
h |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
F1 |
|
|
|
F |
|
F |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
3 |
|
|
|
|
F |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m1 F1h1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m2 F2h2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m3 |
|
|
m3 F3h3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рис. 6.6
При решении плоских задач пара изображается скобкой, стрелка которой указывает направление вращения пары, поскольку направление сил пары, ее плечо и место расположения не существенны, − они могут меняться произвольно, если при этом не меняется момент пары.
|
m2 |
m1 F1h1 |
|
|
|
|
|
m2 F2h2 |
|
m3 |
|
m1 |
|
m3 F3h3 |
|
|
|
Рис. 6.7
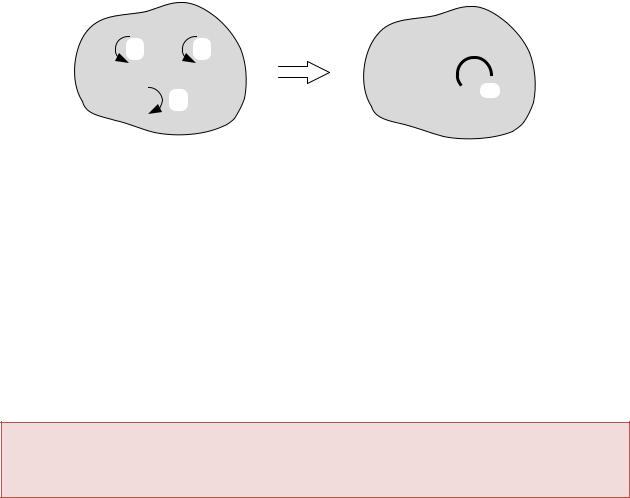
54
Сложение пар сил, лежащих в одной плоскости или в параллельных плоскостях, является частным случаем сложения пар: в этом случае векторное сложение можно заменить алгебраическим сложением:
M m1 m2 m3 F1h1 F2h2 F3h3
Если пары лежат в одной плоскости, то путем суммирования их можно заменить одной эквивалентной парой, момент которой назовем
результирующим алгебраическим моментом системы пар.
Результирующий алгебраический момент системы пар, расположенных в одной плоскости, равен сумме алгебраических моментов составляющих пар:
|
= ∑ |
. |
(6.6) |
|
=1 |
|
|
m1 m3
m2  M
M
Рис.6.8
Система пар находится в равновесии только в том случае, когда результирующий момент равен нулю. Таким образом,
для равновесия пар сил, действующих на твердое тело в одной плоскости, необходимо и достаточно, чтобы сумма алгебраических моментов этих пар была равна нулю, то есть
n |
|
mi 0. |
(6.7) |
i 1
Тема 7.
ПРОИЗВОЛЬНАЯ ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
7.1. ЛЕММА ПУАНСО О ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ СИЛЫ
Рассмотрим теперь самый общий случай — систему, состоящую из любого количества сил, как угодно расположенных в пространстве.

55
Для краткости будем называть такую систему произвольной пространственной системой сил.
Прежде чем перейти к ее преобразованию, приведем вспомогательную теорему (лемму Пуансо) о параллельном переносе силы.
Луи Пуансо (Louis Poinsot, 1777-1859) — французский математик и механик, автор геометрической статики (1803). Ввел в механику понятия момента силы, пары сил, разработал теорию пар и метод приведения системы сил. Многое сделал в кинематике и динамике.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть дана сила , приложенная в точке A (рис. 7.1а). |
|
|
|
|
|
|||||||||||||||||||||
Приложим к точке |
|
B две силы: |
|
|
′ |
и |
|
′′ |
, |
равные по величине и |
||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
′ |
′′ |
), что допускается в соответствии с |
|||||||||||||||
противоположно направленные ( |
= − |
|
||||||||||||||||||||||||
|
|
|
′ |
|
′′ |
) |
|
≡ 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
аксиомой 2, поскольку ( |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Параллельный перенос силы в пространстве |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
MO F |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
||
|
B |
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
F |
|
|
|
|
|
|
|
F |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
r |
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
||||||||
A |
F |
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Рис. 7.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и параллельны ей (рис. 7.1). |
|
|
|||||||||||||
Пусть по модулю они будут равны силе |
|
|
||||||||||||||||||||||||
Полученная система сил |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
, геометрически |
||||||||||
|
|
представляет собой силу |
||||||||||||||||||||||||
равную силе |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′′ |
), |
, приложенную в центре приведения |
B и пару сил (, |
|
||||||||||||||||||||||||
|
|
|
|
|
′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
момент которой равен (, |
|
) = × . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Поскольку выполненные преобразования эквивалентны, то |
|
|
||||||||||||||||||||||||
|
|
|
|
′ |
|
|
′′ |
)) |
′ |
|
|
|
|
|
′′ |
)). |
|
|
|
|
|
|
|
|||
|
≡ |
(, ( |
, |
|
|
≡ ( |
, (, |
|
|
|
|
|
|
|
|
|||||||||||
Добавляемая пара сил называется присоединенной парой.
Момент присоединенной пары, добавляемой при приведении силы F к центру B , равен моменту силы F относительно выбранного центра B :
(, ′′) = ().

56
ДОКАЗАНА ЛЕММА ПУАНСО:
силу можно переносить на параллельную линию действия,
добавляя при этом присоединенную пару, момент которой равен моменту силы относительно новой точки приложения силы.
Операция переноса силы в заданную точку называется приведением силы к заданному центру.
7.2. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ МЕТОДОМ ПУАНСО
Если рассматривается система сил, то все силы (пользуясь леммой Пуансо) можно привести к некоторому центру. В результате этого исходная система сил упростится.
F1
а
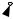 A1
A1
Fn 
An  rn
rn
r1 |
A2 |
|
r2
O |
F2  б
б
 F2
F2
F1 Fn
O 
m1
mn |
m |
|
2 |
Рис. 7.2
ОСНОВНАЯ ТЕОРЕМА СТАТИКИ (ТЕОРЕМА ПУАНСО)
Любая система сил при приведении к произвольному центру заменяется одной силой и одной парой. При этом сила равна главному вектору системы сил и приложена в центре приведения, а пара имеет момент, равный главному моменту системы сил относительно центра приведения.
ДОКАЗАТЕЛЬСТВО
Рассмотрим произвольную систему сил (1, 2, … , ) (рис. 7.2., а).

57
Следуя методу Пуансо, каждую силу системы приведем к центру О, добавляя (рис. 7.2, б) при каждом переносе присоединенную пару с моментом = ( × ), который равен моменту данной силы относительно точки О:
= ( )
Образовавшуюся в точке О систему сходящихся сил (рис. 7.3) заменим одной силой, которая равна главному вектору системы:
|
= ∑ |
|
|
(7.1) |
|
=1 |
|
||
|
|
|
|
 R*
R*
O 
M O*
Рис. 7.3
Систему присоединенных пар заменим одной парой (рис. 7.3), момент которой равен сумме моментов присоединенных пар mi и следовательно, равен главному моменту системы сил:
∑ |
|
= ∑ |
|
|
|
|
. |
(7.2) |
=1 |
=1 |
|
( ) = |
|||||
|
|
|
|
|
|
|
||
Теорема доказана.
СЛЕДСТВИЕ:
две системы сил, имеющие одинаковые главные векторы и одинаковые главные моменты относительно одного и того же центра, эквивалентны друг другу.
7.3.УСЛОВИЯ УРАВНОВЕШЕННОСТИ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ
Сформулируем теперь условия, при которых произвольная пространственная система сил будет уравновешенной.
58
Система сил в общем случае заменяется одной силой и одной парой, но сила и пара не могут уравновесить друг друга.
Следовательно, для уравновешенности системы сил требуется, чтобы и сила, и момент пары были нулевыми.
Отсюда получаются приведенные ниже в трех формах условия уравновешенности произвольной пространственной системы сил.
Для того чтобы произвольная пространственная система сил была уравновешенной, необходимо и достаточно, чтобы выполнялись следующие условия:
1.В векторной форме:
главный вектор системы сил и главный момент системы сил относительно некоторой точки должны быть равны нулю:
|
|
|
|
|
|
|
∑ |
|
|
|
|
{ |
|
= 0 |
или |
{ |
|
|
= 0 |
(7.3) |
|||
|
|
|
|
=1 |
|
|
|||||
|
|
= 0, |
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
( ) = 0, |
|
||
|
|
|
|
|
|
|
|
|
|||
2.В геометрической форме:
многоугольники сил и моментов должны быть замкнуты.
3.В аналитической форме:
суммы проекций сил на каждую из координатных осей и суммы моментов сил относительно каждой из координатных осей должны быть равны нулю:
|
|
|
|
|
|
|
|
∑ |
|
= 0 |
|
|||
|
|
= 0 |
|
|
|
|
|
=1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
∑ |
|
= 0 |
|
||||
|
|
= 0 |
|
|
|
|
|
|||||||
|
{ |
|
|
|
|
=1 |
|
|
|
|
||||
|
|
= 0 |
|
|
|
|
∑ |
|
|
= 0 |
|
|||
|
|
|
или |
{ |
=1 |
(7.4) |
||||||||
|
|
= 0 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
∑ |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
( ) = 0 |
|
||||
|
{ = 0 |
|
|
|
=1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
{∑ |
|
|
|
|
|
||||
|
|
= 0, |
|
=1 |
|
( ) = 0 |
|
|||||||
{ |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
∑ |
|
|
|
|
|||||
|
|
|
|
{ |
=1 |
|
( ) = 0, |
|
||||||
|
|
|
|
|
|
|
|
|
||||||
Таким образом, в статике для произвольной пространственной системы сил в общем случае можно составить шесть уравнений равновесия.
