9480

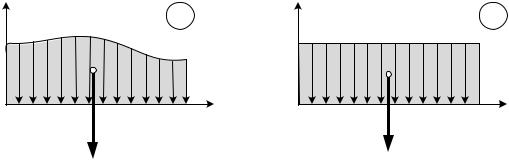
29

3.6. РАСПРЕДЕЛЕННЫЕ СИЛЫ

Понятие о силе, приложенной в точке, является идеализацией реальности. На самом деле взаимодействие тел всегда происходит по некоторой площадке или даже по объему (как у гравитационных сил).

Говоря о сосредоточенной силе, которая приложена в точке, мы на самом деле имеем в виду равнодействующую некоторой силы, распределенной на участке поверхности, размер которого очень мал и в расчёте может не учитываться.

Вмеханике рассматриваются три вида моделей распределенных сил:

1)силы, распределенные вдоль линии;

2)силы, распределенные по поверхности, и

3)силы, распределенные по объему.

Рассмотрим первые два случая.

СИЛЫ, РАСПРЕДЕЛЕННЫЕ ВДОЛЬ ЛИНИИ

Сила, распределенная вдоль линии, характеризуется ее интенсивностью q , которая определяется величиной силы, приходящейся на единицу длины (на 1м) и измеряется в Н/м.

Величина интенсивности может быть переменной q q x (рис. 3.7, а) или постоянной q const (рис. 3.7, б).

Рис. 3.7

В общем случае, когда сила на участке (О, l ) распределена по произвольному закону q q x , ее равнодействующая Q должна быть

вычислена как интеграл. Линия действия равнодействующий Q проходит через центр тяжести подграфика интенсивности, положение которого неизвестно.

Рассмотрим частные случаи.

30

РАВНОМЕРНО РАСПРЕДЕЛЕННАЯ СИЛА

Если интенсивность постоянна q = const (см. рис. 3.7, б), то ее равнодействующая равна Q ql и приложена посередине участка распределения.

СИЛА, ИНТЕНСИВНОСТЬ КОТОРОЙ МЕНЯЕТСЯ ПО ЛИНЕЙНОМУ ЗАКОНУ

Рис. 3.8

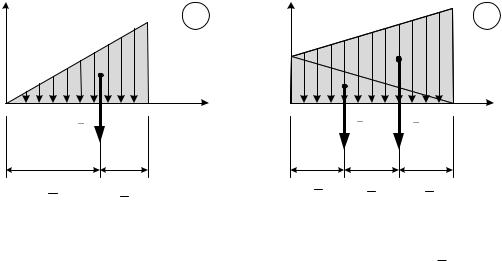
В этом случае (рис. 3.8, а) соответствующий интеграл дает Q 12 ql,

и равнодействующая будет проходить на расстоянии 2l/3 от вершины треугольника интенсивности и на расстоянии l/3 от его основания.

Аналогично определяется равнодействующая, если с ростом координаты х интенсивность убывает от qmax до нуля.

СИЛА, ИНТЕНСИВНОСТЬ КОТОРОЙ МЕНЯЕТСЯ ПО

ЛИНЕЙНОМУ ЗАКОНУ ОТ Q1 ДО Q2

В этом случае (рис. 3.8, б) силу удобно разбить на две распределенные силы, рассмотренные в пункте 2 (на рисунке разбиение показано штрихом).

Тогда исходная распределенная сила заменится двумя силами, линии действия которых делят участок (О, l ) на три равные части.

СИЛЫ, РАСПРЕДЕЛЕННЫЕ ПО ПОВЕРХНОСТИ

Интенсивность такой силы называется давлением р и измеряется в паскалях: 1 Па = 1 Н/м2.

В простейшем случае равномерно распределенной силы (рис. 3.9) на

31

некотором участке поверхности ее равнодействующая будет равна, как известно, произведению давления на площадь этого участка А: F pA и будет проходить через центр тяжести этого участка поверхности.

Рис. 3.9

В более сложном случае для определения равнодействующей требуется вычисление интеграла по площади.

Тема 4.

СХОДЯЩИЕСЯ СИСТЕМЫ СИЛ

4.1. ПРИВЕДЕНИЕ СХОДЯЩЕЙСЯ СИСТЕМЫ СИЛ К РАВНОДЕЙСТВУЮЩЕЙ

Сходящейся системой сил называются совокупность сил, линии действия которых пересекаются в одной точке, которую бедем называть

точкой схода системы.

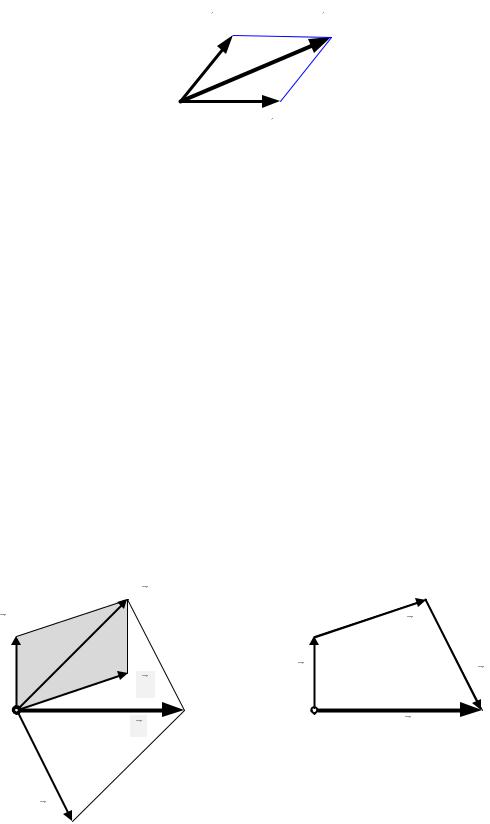
Простейшая система сходящихся сил (две силы) была рассмотрена в аксиоме параллелограмма сил (см. рис. 4.1), где говорилось, что их равнодействующая изображается диагональю параллелограмма, построенного на этих силах, и что она проходит через точку пересечения линий действия исходных сил.

32

Применение аксиомы параллелограмма можно обобщить на случай действия нескольких сходящихся сил.

Так, на рисунке 4.2 показано, что при наличии трех сил мы можем сначала определить равнодействующую первых двух сил:

≡ (1, 2),

а затем, снова применяя аксиому параллелограмма, найти равнодействующую сил и 3, линия действия которой также пройдет через точку О:

≡ (, 3) ≡ (1, 2, 3).

По мере добавления новых сил можно каждый раз вновь использовать аксиому параллелограмма, предварительно перенося силы в точку схода системы. Каждый раз мы будем получать силу эквивалентную всей системе и, следовательно, являющуюся ее равнодействующей.

F3

Рис. 4.2.

Линия действия полученной таким образом равнодействующей будет проходить через точку схода системы, а сама она будет равна геометрической

33

сумме сил системы, то есть главному вектору:

Главный вектор, как известно, можно найти либо аналитически, либо путем построения силового многоугольника (рис. 4.2, б)

Итак, как показано на рис. 4.3,

система сходящихся сил всегда имеет равнодействующую, которая геометрически равна главному вектору этой системы и приложена в точке схода системы.

F1

F1

O

F4 F2

F3

Рис. 4.3

Это справедливо только для сходящихся систем сил.

Для других систем сил равнодействующая может определяться иначе. Существуют системы сил, которые вообще не имеют

равнодействующей, что означает, что такие системы сил невозможно заменить одной силой.

Но нужно помнить, что

если для какой-то системы сил равнодействующая существует, то она геометрически всегда равна главному вектору.

Отсюда следует, что проекции равнодействующей сходящейся системы сил определяются так же, как и проекции главного вектора:

Модуль равнодействующей равен:

34

а ее направляющие косинусы определяются по формулам:

4.2. УСЛОВИЯ УРАВНОВЕШЕННОСТИ СХОДЯЩЕЙСЯ СИСТЕМЫ СИЛ

Система сходящихся сил эквивалентна одной силе, которая по определению является равнодействующей:

≡ (1, 2, … , ).

В общем случае сходящаяся система не является уравновешенной. Исключение составляет случай, когда равнодействующая, а

следовательно и главный вектор этой системы сил равны нулю.

Равнодействующая сходящейся системы геометрически равна ее главному вектору = = ∑=1 , который приложен в точке схода системы.

Отсюда следует

ВЫВОД:

Для равновесия системы сходящихся сил, необходимо и достаточно, чтобы выполнялись следующие условия:

1.В векторной форме:

главный вектор системы сил должен быть равен нулю

2. В геометрической форме:

силовой многоугольник должен быть замкнут.

3. В аналитической форме:

сумма проекций сил на каждую из координатных осей должна быть равна нулю.

Для системы сходящихся сил в пространстве получаем три уравнения равновесия:

36

F 2

Рис. 4.2

ПРИМЕЧАНИЕ

Теорема о трех силах дает только необходимое условие равновесия, без которого равновесие в принципе невозможно. Достаточным условием является замкнутость силового треугольника.

Тема 5.

МОМЕНТЫ СИЛЫ

5.1. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ

Величина и направление силы характеризуют действие силы в том случае, если она придает какому-либо телу поступательное движение.

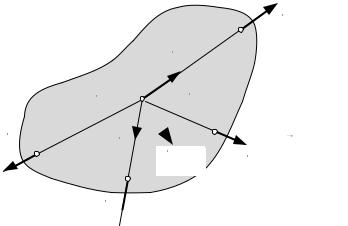
Вращательный эффект силы по отношению к некоторой точке или оси учитывает другая характеристика — момент силы.

Моментом силы относительно некоторой точки О называется величина (), равная векторному произведению радиус-вектора, проведенного из данной точки в точку приложения силы, на саму эту силу :

37

MO F OAB

Рис. 5.1

Направление и модуль момента силы определяются по обычному правилу векторного произведения.

НАПРАВЛЕНИЕ МОМЕНТА СИЛЫ

Вектор-момент силы () перпендикулярен плоскости, проведенной через линию действия силы и точку О (рис. 5.1), и направлен так, чтобы, глядя навстречу ему, видеть силу, стремящейся повернуть эту плоскость против часовой стрелки (правило «правого винта»).

МОДУЛЬ МОМЕНТА СИЛЫ

Модуль векторного произведения:

Модуль момента силы относительно точки равен произведению модуля силы на ее плечо. Плечом силы называется кратчайшее (длина перпендикуляра) расстояние от точки до линии действия силы.

Единица измерения модуля момента силы - [M]= Нм. Из формулы (5.2) следует, что

1.момент силы относительно точки равен нулю только в том случае, когда ее плечо равно нулю, т. е. когда линия действия силы проходит через эту точку;

2.момент силы не зависит от того, где взята точка приложения силы на линии ее действия;

38

3.модуль момента силы равен удвоенной площади треугольника, для которого сила является основанием, а плечо высотой (рис. 5.1).

АНАЛИТИЧЕСКОЕ ВЫРАЖЕНИЕ МОМЕНТА СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ

Это есть аналитическое выражение момента силы относительно точки О.

5.2. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ

Моментом силы относительно некоторой оси z называется скалярная величина (), равная проекции (рис. 5.2) на эту ось

момента силы, вычисленного относительно какой-либо точки О этой оси: