9017

20

Радиус-вектором произвольной точки M называют вектор OM , а его коорди-

наты называют координатами этой точки.

Свойства координат вектора

Пусть векторы a и b в прямоугольной декартовой системе координат заданы своими координатами, то есть a a1 , a2 , a3 , b b1 ,b2 ,b3 , тогда:

b1

1)a b a2 b2 ;a3 b3

2)a a1 , a2 , a3 ;

3)a b a1 b1; a2 b2 ; a3 b3 ;

4)a b a1 b1; a2 b2 ; a3 b3 ;a1

Пример. Найти координаты вектора c 2a b, его длину и направляю-

щие косинусы, если a 1; 2;3 , b 1;0;1 .

Решение:

1) 2a 2 1; 2 2; 2 3 2; 4;6 .

c2a b 2; 4;6 1;0;1 2 1 ; 4 0;6 1 1; 4;7 .

2)c 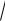12 42 72 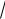66 .

21

Пример. Лежат ли три точки А(2;0;-3), В(-5;4;2) и С(16;-8;-13) на одной прямой?

Решение. Точки А, В и С лежат на одной прямой тогда и только тогда,

когда и векторы AB и AC лежат на одной прямой, то есть коллинеарны.

Найдем координаты этих векторов и проверим векторы на коллинеар-

ность.

AB { 5 2; 4 0; 2 ( 3)} { 7;4;5} ,

AC {16 2; 8 0; 13 ( 3)} {14; 8; 10}.

Согласно свойству 6 координат векторов

Значит, и точки А, В и С лежат на одной прямой.

Ответ: точки А, В и С лежат на одной прямой.

Пример. Даны три последовательные вершины параллелограмма А(2;0;- 3), В(-5;4;2) и С(16;-8;-13). Найти координаты четвертой вершины.

Решение. Пусть D(x; y; z) - четвертая вершина параллелограмма ABCD.

Очевидно, что AB DC . Найдем координаты этих векторов:

AB { 5 2; 4 0; 2 ( 3)} { 7;4;5} ,

DC {16 x; 8 y; 13 z}.

Тогда в силу 1 свойства координат вектора, получаем:

Ответ: D(23; 12; 18) .

Пример. Доказать, что векторы a 2;3;1 , b 5;7;0 , c 3; 2;4 не-

компланарны. Разложить вектор d 4;12; 3 по векторам a , b , c .

22

Решение.

1)Докажем методом от противного. Пусть векторы a , b , c - компланарны.

Рассмотрим векторы a 2;3;1 и b 5;7;0 . Они неколлинеарны, так как их координаты не пропорциональны

52 73 10 .

Тогда в силу предположения о компланарности векторов a , b , c ,

вектор c можно выразить через a , b , то есть c x a y b .

y 1

лучаем y 2 - противоречие. Значит, наше предположение о компланарно-

x 4

сти векторов a , b , c - неверно. Следовательно, они некомпланарны.

2) Найдем разложение вектора d x a y b z c : xa x 2;3;1 {2x; 3x; x},

yb y 5;7;0 {5y; 7 y; 0} , zc z 3; 2;4 {3z; 2z; 4z},

тогда x a y b z c {2x 5y 3z; 3x 7 y 2z; x 4z} .

С другой стороны, d 4;12; 3 . Тогда получаем систему:

25

Пользуясь этими формулами, легко получить формулы для нахождения

§ 5. Скалярное произведение векторов

Скалярным произведением двух ненулевых векторов a и b называется число, равное произведению длин векторов на косинус угла между ними и обо-

значается: a b , то есть

Алгебраические свойства скалярного произведения:

1)a b b a .

2)a b a b , R.

3)a b c a b a c.

Докажем это свойство. Рассмотрим a b c np a( b c) a

Если два вектора a и b заданы своими координатами: a a1; a2 ; a3 и b b1;b2 ;b3 , то их скалярное произведение находим по формуле:

26

a b a1 b1 a2b2 a3b3 .

Пример. Найти скалярное произведение векторов 2a и 3b , если

a 1; 2;3 и b 0; 1;1 .

Решение. Координаты векторов 2a и 3b :

2a 2 1; 2;3 2 1; 2 2; 2 3 2; 4;6 ;

3b 3 0; 1;1 3 0; 3 1 ; 3 1 0;3; 3 .

Тогда искомое скалярное произведение равно:

2a 3b 2 0 4 3 6 3 0 12 18 6.

Ответ: 6.

Некоторые приложения скалярного произведения:

1. Длина вектора из определения скалярного произведения вычисляется по формуле:

a b 60 .

Решение. По свойству 4, находим

c c c a 2b a 2b a 2 4a b 4 b 2

22 4 a b cos a b 4 12 4 4 2 1 cos60 4

8 8 12 12 23 .

Ответ: c 23 .

27

2. Угол между двумя ненулевыми векторами a a1; a2 ; a3 и b b1;b2 ;b3 из определения скалярного произведения вычисляется по фор-

муле:

Пример. Найти угол между векторами a i 2 j 2k и b j k .

следовательно, (a b) 90 , то есть a b.

Ответ: 90 .

3. Проекция вектора a на вектор b вычисляется по формуле:

Ответ: np a b 2 .

28

3)Найти длину вектора а 2b 3с , если b {1,2, 5}, c { 1,1,1} .

4)Доказать, что диагонали четырехугольника, координаты вершин которого

А(-4,-4,4), В(-3,2,2), С(2,5,1), Д(3,-2,2), взаимно перпендикулярны.

пендикулярны?

6) Определить угол между векторами a i j и b i 2j 2k.

7)Даны вершины треугольника А(-1,-2,4), В(-4,-2,0), С(3,-2,1). Найти вели-

чину угла ВАС, проекцию вектора АС на вектор АВ .

8)Найти координаты вектора х , если а х 1, в х 2 , с х 3 где а {5, 6,-2}, в {7, 8,-1}, с ={-2,3,0}.

9)Найти угол между диагоналями параллелограмма, построенного на век-

29

13) Найти вектор х , зная, что а х , а {1,0,1}, b х , b {0,2, 1}, проекция

вектора х на вектор c {1,2,2} равна 1.

14) Найти работу равнодействующих сил F1 1, 1,1 и F 2 2,1,3 при перемеще-

ния её точки приложения из начала координат в точку М(2,-1,-1).

Элементы аналитической геометрии на плоскости

Геометрия одна из самых древних наук. В переводе с греческого слово «гео-

метрия» означает «землемерие» («гео» – по-гречески земля, а «метрео» – ме-

рить). Такое название объясняется тем, геометрия возникла на основе практи-

ческой деятельности людей (разметке земельных участков, проведении дорог,

строительстве зданий и других сооружений и т.д.) и в начале своего развития служила преимущественно практическим целям.

§ 1. Прямая на плоскости

Введение на плоскости прямоугольной декартовой системы координат позволя-

ет определять положение точки на плоскости заданием двух чисел – ее коорди-

нат, а положение прямой на плоскости определять с помощью уравнения (то есть равенства, связывающего координаты точек прямой).

Каждая прямая на плоскости Oxy определяется линейным уравнением первой степени с двумя неизвестными. Обратно: каждое линейное уравнение первого порядка с двумя неизвестными определяет некоторую прямую на плоскости.

Уравнение прямой позволяет изучение геометрических свойств прямой заме-

нить исследованием ее уравнения. Так, для того, чтобы установить лежит ли точка M 0 (x0, y0 ) на прямой F(x, y) 0 , достаточно проверить (не прибегая к гео-

метрическим построениям) удовлетворяют ли координаты точки M 0 уравнению

F(x, y) 0 этой прямой.

Пример 1. Лежит ли точка M 0 1; 2 на прямой l : 3x y 1 0.