
книги / Численные методы решения задач строительства. Ч. 2
.pdf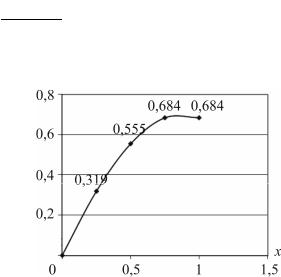
После приведения подобных систему (7.42) можно записать в матричном виде:
1 |
0 |
0 |
0 |
0 |
|
y |
|
|
0 |
|
|
||
|
|
30,94 |
16 |
0 |
0 |
|
|
0 |
|
|
|
|
|
16 |
|
|
y1 |
|
|
1 |
|
||||||
|
0 |
16 |
30,75 |
16 |
0 |
|
|
|
|
|
|
|
(7.43) |
|
|
y2 |
|
1 |
|||||||||
|
0 |
0 |
16 |
30,43 |
16 |
|
y3 |
|
|
1 |
|
||
|
0 |
0 |
0 |
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
y4 |
|
|
0 |
|
|
|||||
Результат решения этой системы уравнений, соответствующий приближенному решению краевой задачи, можно записать в виде таблицы
xi |
0 |
0,25 |
0,5 |
0,75 |
1 |
уi |
0 |
0,319 |
0,555 |
0,684 |
0,684 |
или представить в виде графика (рис. 7.13).
Рис. 7.13. График изменения изгибающего момента по длине балки
В подразд. 7.3.3 приведено решение этой задачи с использованием электронных таблиц Excel.
31
Сходимость метода конечных разностей
При использовании приближенных разностных методов очень важным является вопрос о сходимости. Понятие сходимости может быть сформулировано по-разному. На практике эффективная оценка погрешности затруднительна. Поэтому при решении инженерных задач, для правильного выбора шага h, используют уже известный метод половинного шага. Находят численное решение задачи на сетке n с шагом h и на сетке 2n с шагом h/2. Если значения полученных решений (двух сеточных функций) в одинаковых узлах отличаются друг от друга не более чем на
5 %, то полученную сеточную функцию на сетке 2n принимают за приближенное решение задачи. В противном случае шаг уменьшают в два раза и повторяют решение.
7.3.3. Решение краевой задачи методом конечных разностей с использованием
электронных таблиц Microsoft Excel
Алгоритм реализации метода конечных разностей рассмотрим на примере краевой задачи (7.41):
y" + (1 + x2) y = –1, y(0) = 0, y'(1) = 0
на отрезке x [1, 2] с шагом h = 0,25 и с шагом h = 0,125. Сравнив полученные результаты, необходимо сделать
вывод о необходимости поиска следующего приближения или о прекращении счета.
Построение первой итерации
1. Подготовим таблицу, как это показано на рис. 7.14. Введем значения исходных данных: a, b, 0 , 1, A, 0 , 1, B ,
n. Первоначальное количество разбивок возьмем n = 4.
32
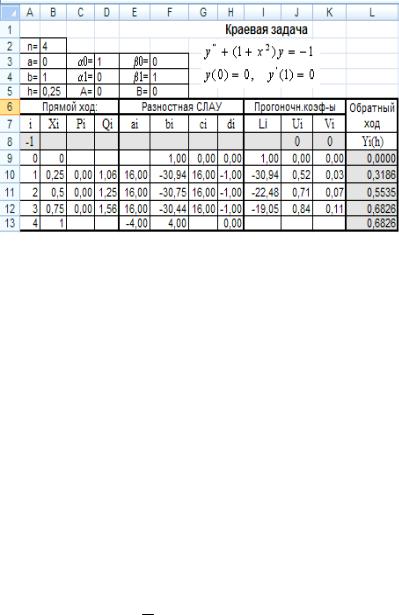
Рис. 7.14. Схема решения краевой задачи (первая итерация h = 0,25)
2. Вычислим шаг разностной сетки h = (b – a)/n
вячейке В5 = (В4 – В3)/В2.
3.Строка 8 остается пока пустой, опишем ее позже.
4.Номер узла i введем с помощью автозаполнения
встолбце А таблицы.
5.Значения узлов разностной сетки определим по
формуле xi = a + h*i, i = 0, 1, …, n. Для этого в ячейку В9 введем формулу В9=$B$3+$B$5*A9 и скопируем ее вниз до конца таблицы (до х = 1).
6.В столбцах C, D таблицы вычислим значения функций p(x) = 0, q(x) = (1 + x2) в узлах сетки xi, для i = 1, 2, .., n – 1 (i = 1, 2, 3).
7.После этого приступим к формированию разностной СЛАУ (7.37). Для этого в столбцах Е, F, G таблицы
вычислим значения коэффициентов аi вi, сi по формулам
(7.38), (7.39), как это показано на рис. 7.14.
8.В столбце Н таблицы сформируем вектор правой
части СЛАУ, вектор D (7.40).
33
Таким образом, разностная система (7.37) сформирована и имеет вид
3y0 |
0 |
|
16y0 30,94y1 16y2 |
1 |
|
16y1 30,75y2 16y3 |
1 |
(7.44) |
16y2 30,75y3 16y4 |
1 |
|
4y4 4y5 |
0 |
|
Теперь можно приступать к ее решению любым известным методом. Поскольку матрица системы является трехдиагональной, то рационально использовать метод прогонки (см. подразд. 3.2.2, ч. I).
Прямой ход метода прогонки. Вычислим прогоночные коэффициенты.
1. Обнулим ячейки J8 K8, т.е. зададим прогоночные
коэффициенты U–1 = 0, V–1 = 0.
2. Вычислим Li и прогоночные коэффициенты Ui, Vi по формулам (i = 0,1, n – 1):
U |
|
|
c |
V |
|
d |
i |
aV |
|
|
i |
i , |
|
|
i i 1 |
, |
|
||||
|
|
|
|
|
||||||
|
|
Li |
i |
|
|
|
Li |
|
(7.45) |
|
|
|
|
|
|
|
|
|
|||
|
|
|
L aU |
b . |
|
|
||||
|
|
|
i |
i i 1 |
|
|
|
i |
|
|
Для этого введем формулы I9=E9*J8+F9; J9=–G9/I9; K9=(H9–E9*K8)/I9 и скопируем их вниз до предпоследнего узла.
3. Обратный ход метода прогонки. Значение неизвестногоyn (n = 4) вычислим вячейке L13 поформуле
yn |
dn an Vn 1 |
. |
(7.46) |
|
|||
|
an Un 1 bn |
|
|
34

Для этого введем формулу
L13=(H13–E13*K12)/(E13*J12+F13).
4. Остальные значения yi, (i = 0,1,2,3) вычислим по формуле
yi Ui yi 1 |
Vi , |
i 1, 2, ..., n 1. |
(7.47) |
5. Для этого в |
ячейку L12 введем |
формулу |
|
L12=J12*L13+K12 и скопируем ее вверх. Полученное решение
Xi |
0 |
0,25 |
0,5 |
0,75 |
1 |
Yi(h) |
0 |
0,319 |
0,553 |
0,683 |
0,683 |
можно принять за первую итерацию, первое приближенное решение исходной краевой задачи (7.41).
Построение второй итерации
Для выполнения второй итерации сделаем сетку вдвое гуще (n = 8, шаг h = 0,125) и повторим приведенный выше алгоритм.
Это можно проделать на этом же листе книги Excel или на другом листе книги Excel (рис. 7.15).
Вторая итерация, вторая сеточная |
функция с |
шагом |
||||||||
h = 0,125 имеет вид |
|
|
|
|
|
|
|
|||
|
|
0,125 |
|
|
|
|
|
|
|
|
Xi |
0 |
0,25 |
0,375 |
0,5 |
0,625 |
0,75 |
0,875 |
|
1 |
|
Yi(h/2) |
0 |
0,209 |
0,4 |
0,568 |
0,71 |
0,823 |
0,902 |
0,9436 |
|
0,944 |
Таким образом, получены два приближенных решения (две итерации) краевой задачи (7.41). Сравнение двух сеточ-
ных функций для двух разностных сеток 10 и 5 (h = 0,125
35
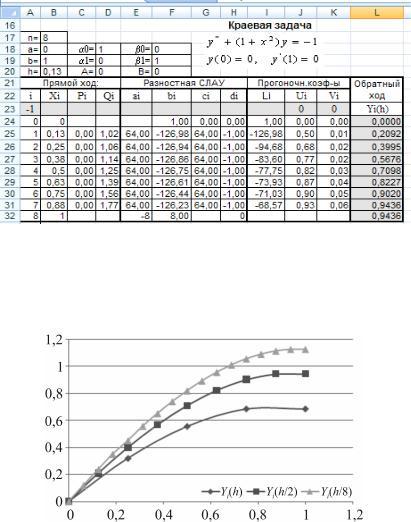
и h = 0,25) показывает, что их расхождение в одинаковых узлах составляет более 5 %. Поэтому необходимо продолжить итерационный процесс для n = 16, т.е. дляh/4 = 0,0625.
Рис. 7.15. Схема решения краевой задачи (вторая итерация h = 0,125)
На рис. 7.16 приведены три приближенных решения нашей краевой задачи (три сеточные функции).
Рис. 7.16. Сравнение результатов трех итераций
36
Как видно из приведенных графиков, итерационный процесс является сходящимся, но решение следует продолжить и построить следующее приближенное решение для n = 32.
Контрольные вопросы
1.Типы дифференциальных уравнений (обыкновенные и в частных производных).
2.Обыкновенные дифференциальные уравнения. Что является решением уравнения? Общее и частное решения.
3.Постановка и методы численного решения задачи Коши. Методы Эйлера и Рунге–Кутта.
4.Постановка краевой задачи. Что является решением краевой задачи? Методы решения.
5.Метод конечных разностей. Конечно-разностная аппроксимация.
6.Сходимость метода конечных разностей.
37

ГЛАВА 8
Вариационный подход к решению краевых задач
Вариационный подход – это применение вариационных методов к решению краевых задач. Он получил широкое распространение после того, как немецкий математик Ритц в 1908 году предложил удобный прием построения приближенного решения вариационной задачи.
Как уже отмечалось, появление ЭВМ обусловило интенсивную разработку численных методов, которые поначалу основывались на дискретизации дифференциальных уравнений (метод конечных разностей). Хорошо разработанные методы строительной механики стержневых систем и удачные реализации их на ЭВМ заинтересовали многих исследователей возможностью расчета пластинчатых и трехмерных (пространственных) систем на основе стержневых аппроксимаций. Настоящую революцию в строительной механике и теории упругости произвело появление метода конечных элементов, открывшего неограниченные возможности компьютерного моделирования и расчета систем практически любой сложности и размерности, в основе которого лежит вариационный подход к решению краевых задач, описываемых как обыкновенными дифференциальными уравнениями, так иуравнениями вчастных производных.
Прежде чем рассматривать вариационные методы решения краевых задач, введем некоторые основные понятия теории вариационного исчисления.
8.1. Основные понятия вариационного исчисления
Основным объектом изучения вариационного исчисления является функционал [3].
38

Функционал – это функция, зависящая от функции,
т.е. аргументом функционала является функция. Примером функционала может служить определенный интеграл
J b f (x)dx , который принимает некоторое числовое зна-
a
чение при подстановке каждой конкретной функции в подынтегральное выражение. Функционал может зависеть от нескольких функций или от функций нескольких независимых переменных.
В вариационном исчислении изучаются методы на-
хождения экстремальных значений функционалов. Задачи,
в которых требуется исследовать функционал на максимум или минимум, называются вариационными задачами.
Методы решения вариационных задач весьма сходны с методами исследования функций на максимум или минимум.
В дифференциальном исчислении [3, 5] рассматривает-
ся доказательство теоремы:
Если дифференцируемая функция f(x) достигает максимума или минимума во внутренней точке x = x0, области определе-
ния функции, то в этой точке
Следовательно, для нахождения экстремума функции вычисляется 1-я производная этой функции и приравнивается к нулю. В результате определяется значение аргумента х0, при котором функция f максимальна или минимальна.
При исследовании функционалов вариация функционала J играет такую же роль, как и дифференциал df при исследовании функций.
В вариационном исчислении [3] также доказывается теорема:
39

Если функционал J[ y(x)] , имеющий вариацию, достигает
максимума или минимума при y = y0(x), где y(x) – внутренняя точка областиопределенияфункционала, то при y = y0(x) J 0 .
Значит, необходимым условием экстремума функционала является обращение в нуль вариации функционала. Процесс варьирования функционалов производится аналогично дифференцированию сложных функций.
Поскольку аргументом функционала является функция, то именно функция y = y0(x), которая называется эстремалью, доставляет экстремум функционалу.
Отметим, что если y(x) доставляет функционалу J минимум, то 2 J 0 , а если максимум, то 2 J 0 .
8.1.1.Связь решения краевой задачи
снахождением минимума функционала
Многие законы механики и физики сводятся к утверждению, что некоторый функционал, связанный с физическим процессом, должен достигать минимального или максимального значения. В такой формулировке эти законы называются вариационнымипринципамимеханики или физики.
Например, вариационный принцип возможных перемещений Лагранжа формулируется так:
Из всех возможных перемещений упругой системы только действительные перемещения сообщают полной потенциальной энергии минимальное значение
или
упругая система находится в равновесии, если сумма работ всех внешних и внутренних сил на любых возможных перемещениях равна нулю.
Аналитическиэтоможнозаписатькак П (U Т) 0 .
Здесь П – полная потенциальная энергия системы
(функционал); U – потенциальная энергия упругой деформации; Т – работа внешних сил.
40
