
книги / Физика для бакалавра. Ч. 1-1
.pdfЧем ближе к единице дробь, выражающая отношение частот колебаний, тем сложнее оказывается фигура Лиссажу. На рис. 7.11 для примера показана кривая для отношения частот 3:4 и разности фаз, равной /2.
121

8. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ГАРМОНИЧЕСКОГО КОЛЕБАНИЯ
Рассматриваемые вопросы. Идеальный гармонический осциллятор. Квазиупругая сила. Уравнение идеального осциллятора и его решение. Маятники. Превращения энергии при колебаниях. Свободные затухающие колебания осциллятора с потерями. Вынужденные колебания. Резонанс.
К динамическим характеристикам гармонического колебания относятся: F – сила; а – ускорение; Ек – кинетическая энергия; Еп – потенциальная энергия.
8.1. Идеальный гармонический осциллятор. Квазиупругая сила. Уравнение идеального осциллятора и его решение
Рассмотрим систему, представляющую собой шарик массой m, подвешенный на нити (данную систему можно рассматривать в качестве идеального гармонического осциллятора). Выведем дифференциальное уравнение данного осциллятора. Сообщим шарику смещение x = A, после чего предоставим систему самой себе. Под действием квазиупругой силы (силы, зависящие от смещения по закону Fx = kx, независимо от их природы называются квазиупругими) шарик будет двигаться к положению равновесия с возрастающей скоростью
v ddxt x.
При этом потенциальная энергия системы будет убывать, но зато появится всевозрастающая кинетическая энергия
Eк mv22 .
122
Достигнув положения равновесия, шарик продолжит движение по инерции. Это движение будет замедленным и прекратится тогда, когда кинетическая энергия полностью перейдет в потенциальную, т.е. когда смещение шарика станет равным ( А). Затем аналогичный процесс будет протекать при движении шарика в обратном направлении. Если трение в системе отсутствует, то полная энергия должна сохраняться и шарик будет двигаться в пределах от х = А до х = А неограниченно долго.
Уравнение второго закона Ньютона для шарика имеет вид
m |
d2 x |
kx. |
(8.1) |
|||||
dt |
2 |
|||||||
|
|
|
|
|
||||
Введя обозначение |
|
|
|
|
|
|
|
|
|
ω02 |
k |
, |
(8.2) |
||||
|
|
|||||||
|
|
|
|
|
m |
|
||
преобразуем уравнение (8.1) следующим образом: |
|
|||||||
d2 x |
|
|
2 |
|
(8.3) |
|||
dt2 |
ω0x 0. |
|||||||
|
|
|
|
|
|
|||
Итак, при отсутствии сил трения движение под действием квазиупругой силы описывается уравнением (8.3). Это уравнение представляет собой дифференциальное уравнение собственных незатухающих колебаний гармонического осциллятора.
Общим решением уравнения (8.3) является
x = A cos (ω0t + α). |
(8.4) |
Следовательно, движение системы (гармонического осциллятора), находящейся под действием силы вида F = kx (квазиупругой силы), представляет собой гармоническое колебание.
Сила прямо пропорциональна смещению и направлена к положению равновесия, т.е. F = kx. Подставив в это выражение значения k и x из (8.2) и (8.4), получим
F = A ω02 cos ( 0 t + ) = ma.
123
Как видно из этого выражения, период и фаза силы совпадают с периодом и фазой ускорения.
Квазиупругая сила является консервативной, поэтому полная энергия гармонического колебания должна оставаться постоянной. В процессе колебаний происходит превращение кинетической энергии в потенциальную и обратно, причем в моменты наибольшего отклонения от положения равновесия полная энергия Е состоит только из потенциальной энергии, которая достигает своего наибольшего значения Еп max :
E Е |
п max |
|
kA2 |
. |
(8.5) |
|
2 |
||||||
|
|
|
|
При прохождении же системы через положение равновесия полная энергия состоит лишь из кинетической энергии, которая в эти моменты достигает своего наибольшего значения Ек max:
|
mv2 |
mA2ω2 |
|
||
E = Eк max= |
max |
|
0 . |
(8.6) |
|
2 |
|||||
|
|
2 |
|
||
Выясним, как изменяются со временем кинетическая и потенциальная энергии гармонического колебания. Кинетическая энергия, с учетом выражения (7.6),
Eк = |
mv2 |
|
mA2ω2 |
sin2 ( 0 t + ). |
(8.7) |
2 |
0 |
||||
|
|
2 |
|
|
Потенциальная энергия
|
kx2 |
kA2 |
|
|
Еп = |
2 |
2 |
cos2 ( 0 t + ). |
(8.8) |
Складывая (8.7) с (8.8) и принимая во внимание, что mω02 k, получим формулу для полной энергии:
E E |
|
E |
|
|
kA2 |
|
mA2ω2 |
(8.9) |
к |
п |
2 |
0 . |
|||||
|
|
|
|
2 |
|
124

8.2.Маятник
Вфизике под маятником понимают твердое тело, совершающее под действием квазиупругой силы колебания вокруг неподвижной точки или оси. Наиболее часто рассматривают математический и физический маятники.
8.2.1.Математический маятник
Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешено тело, масса которого сосредоточена в одной точке и которое совершает колебательное движение под действием силы тяжести. Достаточно хорошим приближением к математическому маятнику служит небольшой тяжелый шарик, подвешенный на длинной тонкой нити.
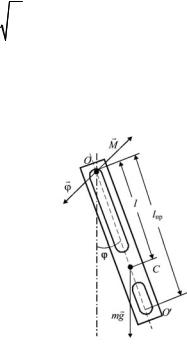
Выведем уравнение движения математического маятника. Отклонение его от положения равновесия будем характеризовать углом , образованным нитью с вертикалью (рис. 8.1).
Рис. 8.1
125

При отклонении маятника от положения равновесия возникает вращательный момент М, равный по величине mglsin (m – масса, l – длина маятника). Этот момент направлен так, что стремится вернуть маятник в положение равновесия, и его действие аналогично действию квазиупругой силы. Поэтому так же, как смещению и квазиупругой силе, проекциям момента М и углового смещения на ось z нужно приписывать противоположные знаки. Следовательно, выражение для вращательного момента имеет вид
M = mgl sin . |
(8.10) |
Запишем для маятника уравнение динамики вращательного движения. Обозначим угловое ускорение через ε d2 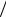 dt2.
dt2.
Учитывая, что момент инерции маятника I = ml2 (момент инерции для материальной точки), получим
ml2 |
d2 |
|
dt2 = mgl sin . |
(8.11) |
Разделив обе части уравнения на (ml) и введя обозначение
g l ω02, |
(8.12) |
выражение (8.11) можно переписать в виде
d2 ω02 |
sin 0. |
(8.13) |
dt2 |
|
|
Ограничимся рассмотрением малых колебаний, тогда можно положить
sin . |
(8.14) |
|
С учетом (8.14) выражение (8.13) примет вид |
|
|
d2 |
2 |
(8.15) |
dt2 |
ω0 0. |
|
|
|
|
126
Уравнение (8.15) представляет собой дифференциальное уравнение колебаний математического маятника. Его решение имеет вид
= A cos( 0 t + ). |
(8.16) |
Следовательно, при малых колебаниях угловое смещение математического маятника изменяется со временем по гармоническому закону.
Как следует из (8.12), частота колебаний математического маятника зависит только от ускорения свободного падения и от длины маятника и не зависит от его массы. Формула (7.2) с учетом (8.12) дает выражение для периода колебаний математического маятника:
T 2π |
l |
. |
(8.17) |
|
|||
|
g |
|
|
8.2.2. Физический маятник
Физическим маятником называется любое твердое тело, способное под действием силы тяжести совершать колебания вокруг неподвижной оси, не совпадающей с его центром инерции (рис. 8.2). По аналогии с уравнением для математического маятника запишем уравнение для физического маятника:
I |
d2 |
|
= mgl sin , (8.18) |
|
dt2 |
||||
|
|
|||
где m – масса маятника; l – расстояние |
|
между точкой подвеса О и центром |
|
инерции С маятника (см. рис. 8.2). Знак |
|
минус в выражении (8.18) имеет то |
|
же значение, что и в формуле (8.10). |
Рис. 8.2 |
|
127
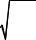
Вслучае малых колебаний выражение (8.18) переходит
вуже известное нам уравнение
d2 ω02 0. |
(8.19) |
dt2 |
|
В данном случае |
|
ω02 mgl . |
(8.20) |
IO |
|
Момент инерции физического маятника относительно оси, проходящей через точку подвеса, можно представить в виде
I |
O |
mgl . |
(8.21) |
|
ω02 |
|
Выражение (8.19) представляет собой дифференциальное уравнение колебаний физического маятника. Решение уравнения (8.19) имеет вид
= 0 cos ( 0 t + ). |
(8.22) |
Из уравнения (8.22) следует, что при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания, частота которых зависит от массы маятника, момента инерции маятника относительно оси вращения и расстояния между осью вращения и центром инерции маятника. В соответствии с (8.20) период колебания физического маятника определяется выражением
T 2π |
IO |
. |
(8.23) |
|
|||
|
mgl |
|
|
Приведенной длиной физического маятника называется длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника. Из сопоставления формул (8.17) и (8.23) следует, что приведенной длиной физического маятника будет выражение
128
lпр = |
IO |
. |
(8.24) |
|
|||
|
ml |
|
|
Точка на прямой, соединяющей точку подвеса с центром инерции, лежащая на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника (см. точку О на рис. 8.2).
Точка подвеса и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания.
8.3. Свободные затухающие колебания осциллятора с потерями
Основными характеристиками затухающего колебания являются: – коэффициент затухания; – декремент затухания;
– логарифмический декремент затухания.
Во всякой реальной колебательной системе имеются силы сопротивления, действие которых приводит к уменьшению энергии системы. Если убыль энергии не восполняется за счет работы внешних сил, то колебания будут затухать. В простей-
шем случае сила сопротивления Fx пропорциональна величине скорости:
F r dx , |
(8.25) |
x dt
здесь r постоянная величина, называемая коэффициентом сопротивления среды; знак минус обусловлен тем, что сила Fx и
скорость v имеют противоположные направления, поэтому их проекции на ось х имеют разные знаки.
Уравнение второго закона Ньютона при наличии сил со-
противления имеет вид |
|
|
|
|
|
|
|
m |
d2x |
kx r |
dx |
. |
(8.26) |
||
dt |
2 |
dt |
|||||
|
|
|
|
||||
|
|
|
|
|
|
129 |
|
Применив обозначение
2 mr , ω02 mk
(r коэффициент сопротивления среды, т.е. коэффициент пропорциональности между скоростью dx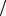 dt и силой сопротивле-
dt и силой сопротивле-
ния; k – коэффициент квазиупругой силы; 0 – собственная частота колебания системы), перепишем уравнение (8.26) следующим образом:
d2x |
2β |
dx |
2 |
(8.27) |
dt2 |
dt |
ω0x 0. |
||
|
|
|
Это дифференциальное уравнение описывает затухающие колебания системы.
При не слишком сильном трении общее решение уравнения (8.27) имеет вид
x = A0 e t cos ( t + ), |
(8.28) |
здесь А0 и произвольные постоянные; частота, с которой система совершает затухающие колебания,
ω |
ω02 β2 . |
|
|
(8.29) |
|
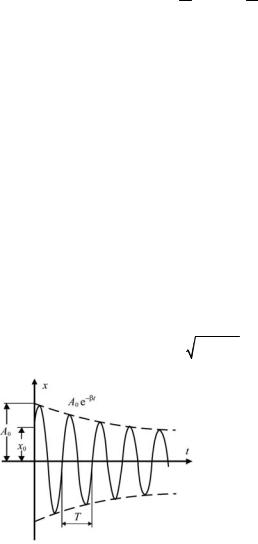
На рис. 8.3 представлен |
|||
|
график функции (8.28). Пунк- |
|||
|
тирными |
линиями |
показаны |
|
|
пределы, в которых находится |
|||
|
смещение колеблющейся точ- |
|||
|
ки х. |
|
|
|
|
В |
соответствии с видом |
||
|
функции (8.28) движение си- |
|||
|
стемы |
можно рассматривать |
||
Рис. 8.3 |
как гармоническое |
колебание |
||
частоты |
с амплитудой, из- |
|||
|
меняющейся по закону |
|||
130
