книги / Оптимальное проектирование конструкций.-1

группы. К первой группе относят задачи оптимизации, для которых критерий качества и ограничения выражаются через интегралы от искомых функций. При этом ограничения имеют вид «изопериметрических» равенств и неравенств. К интегральным характеристикам относятся вес, податливость, сила потери устойчивость, частота и т.д. Ко второй группе относят задачи, для которых критерий качества и рассматриваемые ограничения имеют локальный характер. К этой же группе относят и смешанные задачи, когда в рассмотрение принимаются как интегральные, так и локальные характеристики конструкции, например, максимальное смещение и максимальное значение интенсивности напряжений.

Большая часть полученных в теории оптимального проектирования результатов относится к задачам первой группы. Это объясняется прежде всего тем, что для решения задач с интегральными характеристиками используются известные методы классического вариационного исчисления.

При решении же задач второй группы основная трудность заключается в следующем. Например, если решается задача минимизации максимального прогиба пластинки и отыскания оптимального распределения ее толщины, то определение необходимых условий оптимальности и их численная реализация осложнены тем, что заранее неизвестна точка максимального прогиба. Положение же этой точки существенно зависит не только от вида нагрузки, но и от искомого распределения толщины.

Рассмотрим статические задачи только первой группы. Обозначим через u = [u1(x), …, um(x)] вектор-функцию, определяющую состояние кон-

струкции, а через h = [h1(x), …, hn(x)] – вектор-функцию параметров проектирования. Критерий качества конструкции представим в виде

где φk = const.

Напряженно-деформированное состояние конструкции определяется системой дифференциальных уравнений

L u = q

c краевыми условиями на границе N u Г = 0.

Такая постановка соответствует изопериметрической задаче вариационного исчисления, решение которой, как известно, можно получить c учетом необходимых условий оптимальности (уравнений Эйлера) для функционала

131

где числа λ k – множители Лагранжа.

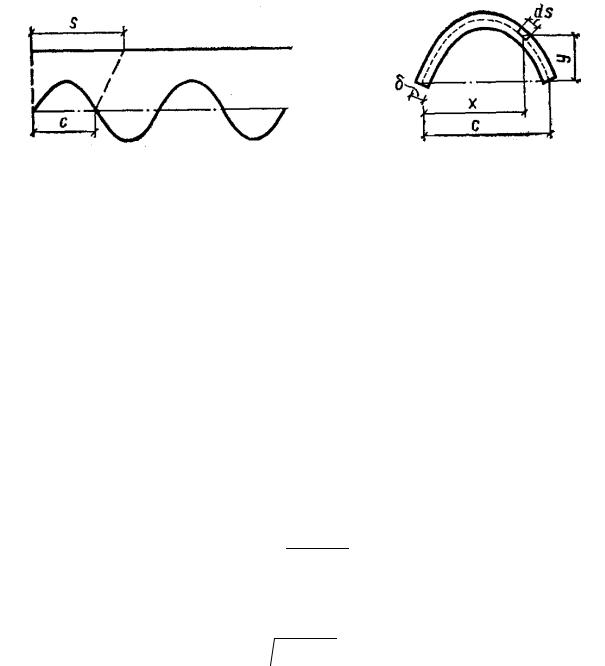
Пример 5.1. Требуется запроектировать волнистый настил [13] наибольшей несущей способности (рис. 5.1).

Рис. 5.1

Для изготовления волнистого настила шириной nc имеется лист материала толщиной δ и шириной ns (n – заданное число полуволн). Предполагая очертания нижней и верхней частей сечения и пределы текучести материала на сжатие и растяжение одинаковыми, найти наиболее выгодную форму профиля настила при расчете его по предельной несущей способности.

Р е ш е н и е . Наиболее выгодной будет та форма профиля, при которой пластический момент сопротивления сечения настила (одной волны) будет максимальным, т.е.

где y(x) – вертикальная координата дуги сечения; s – длина дуги полови-

ны волны настила.

Перейдем к декартовой системе координат, тогда

ds = 1 + ( y′)2 dx

и критерий (5.4) с точностью до множителя 2δ примет вид

c

∫ y 1 + ( y′)2 dx max .

0

Кроме того, должно выполняться дополнительное условие

132

где A = 1/ C, а В – новая произвольная постоянная интегрирования. Общее решение поставленной задачи имеет вид

y = A ch x + B − λ . A

133

Таким образом, дуга сечения волнистого настила наибольшей несущей способности должна иметь вид гиперболической косинусоиды, т.е. цепной линии (5.8), где постоянную А можно найти из условия (5.9).

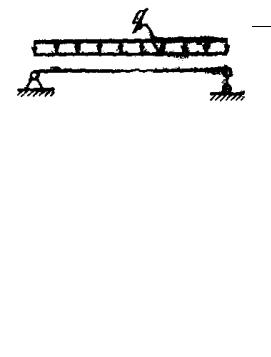
Пример 5.2. Минимизация веса шарнирно закрепленной балки прямоугольного профиля [17]. Пусть балка прямоугольного профиля шарнирно оперта в точках х = 0 и х = l и изгибается под действием поперечной распределенной нагрузки (рис. 5.2). Ширина сечения b. Опре-

делить, при каком законе изменения высоты сечения h(x) вес балки минимален, если максимальный прогиб не превышает заданной величины f.

Ре ш е н и е . Обозначим момент от единичной силы, приложенной

вместе максимального прогиба, через М1(х). Если Mq – момент от внешней нагрузки, то согласно формуле Мора прогиб

При этом объем балки должен быть минимальным, т.е.

l

∫bh(x)dx min .

−l

134

Моменты М1(х) и Mq можно выразить через безразмерную координату ξ :

Получили изопериметрическую вариационную задачу

Сведем ее к задаче на безусловный минимум с помощью множителя Лагранжа λ :

Подставив полученное соотношение во второе уравнение (5.10), найдем

В результате получим формулу для оптимальной высоты сечения

h = 0,503a−1/ 3[ξ 2 (1 − ξ )1/ 4 ].

Если ставятся ограничения как по прочности, так и по деформациям, то вариационное исчисление становится малоэффективным и для решения задачи можно использовать принцип максимума.

Задачи для самостоятельного решения

Решить задачи минимизации веса балки при заданных максимальных прогибах при заданных видах нагружения (рис. 5.3, а, б, в).

Рис. 5.3

135

5.2. Теория оптимального управления

Исследования по оптимизации конструкций проводятся главным образом по двум различным направлениям. Первое из них, называемое иногда структурным синтезом, относится к оптимизации дискретных или дискретизируемых систем. При этом возникает задача математического программирования по определению экстремума функции цели при ограничениях в форме равенств или неравенств.

Вэтих задачах хотя и можно рассматривать относительно сложные конструкции, но все же число параметров проектирования остается ограниченным по сравнению с требованием практики.

Другое направление исследований посвящено оптимальному проектированию элементов с распределенными параметрами, свойства которых описываются обыкновенными (одномерные конструкции) дифференциальными уравнениями или уравнениями в частных производных.

Вжизни любая система – это система с распределенными параметрами, а потому такая модель (описание) по природе своей ближе к реальной конструкции. Теоретические основы второго направления заложены в вариационном исчислении и теории оптимального управления.

Аппарат классического вариационного исчисления при всей своей фундаментальности не позволяет найти решения целого ряда вариационных задач. Такие задачи еще называются вариационными задачами неклассического типа. Основной класс таких задач и составляют задачи оптимального управления. Например, в области космической механики это задачи возможности попадания в заданную точку или в космическое пространство за минимальное время, в заданный момент – в заданную область пространства с заданной скоростью и с максимальным весом аппарата или

сминимальной затратой энергии; о возможности достижения определенной скорости за минимальное время и т.п.

Выдающуюся роль в развитии теории оптимального проектирования сыграл академик Л.С. Понтрягин, который сформулировал необходимые условия оптимальности (принцип максимума), являющиеся математической основой теории оптимального управления. Это послужило мощным толчком как в развитии современной теории экстремальных задач, так и в создании численных методов решения таких задач.

5.2.1. Постановка задач оптимального управления

Обычно постановку задач оптимального управления начинают с простейшего примера движения автомобиля. Рассмотрим прямолинейное движение автомобиля. В каждый момент времени положение автомобиля можно охарактеризовать двумя величинами: пройденным расстоянием b и

136

скоростью движения v, которые меняются со временем, но не произвольно, а сообразно воле водителя, способного по своему желанию увеличивать или уменьшать развиваемую двигателем силу F. Таким образом, мы имеем связанные между собой параметры b, v, F (рис. 5.4). Величины b, v, характеризующие состояние автомобиля, называют фазовыми координатами, а

торые меняются со временем, причем этим изменением (движением объекта) можно управлять с помощью «рулей», положение которых характери-

зуется в каждый момент времени функциями u1, u2, …, um. «Рулями» можно манипулировать, т.е. по своему желанию их можно менять (конечно, в допустимых пределах). Если мы знаем начальное положение объекта, т.е.

xj (t0) = xj0 и выбираем ui (t) для всего рассматриваемого отрезка времени,

то по уравнениям движения однозначно можно определить xj (t), которое уже не зависит от нашего желания, но на движение объекта мы можем воздействовать выбором ui (t).

Одна из задач управления может быть сформулирована, например, следующим образом: в начальный момент t = t0 объект находится в со-

стоянии х0(х1(t0), x2(t0), …, xn(t0)). Требуется выбрать такое управление u(t), которое переведет объект в заранее заданное конечное состояние, не совпадающее с начальным, причем это перемещение должно быть в некотором смысле оптимальным, например, на это перемещение должно затрачиваться минимальное время (если спешим) или при этом мы должны расходовать минимум топлива (режим экономии) и т.д.

Существенным моментом, характеризующим управляемую систему, является описание множества допустимых управлений, т.е. совокупность таких функций u(t), которые, исходя из реальных обстоятельств рассматриваемой задачи, разрешается выбрать в качестве управлений и среди которых мы будем в дальнейшем искать оптимальное управление. Это множество задают, как правило, с помощью условий, накладываемых на возможные значения функции u(t), и требований к ее свойствам.

В любом реальном объекте «рули» не могут занимать произвольные положения либо из-за конструктивных особенностей объекта и ограниченности ресурса, либо из-за условий эксплуатации объекта, опасности нару-

137

шения его нормальной работы. Это означает, что в пространстве управляющих параметров выделено некоторое множество U, называемое областью управления. В любой момент времени u(t) должна принадлежать этому множеству, т.е. для любого времени t верно соотношение u(t) U, называемое ограничением на управление. Самым типичным является случай, когда область управления U – ограниченное замкнутое множество (например, для автомобиля, это мощность двигателя) и управление занимает свое «крайнее» положение (max или min).

Помимо ограничения на значение управляющего вектора в каждый момент времени необходимо также выяснить допустимый характер изменения этого вектора с течением времени. Обычно в качестве управлений рассматривают кусочно-непрерывные функции, т.е. вектор-функция u(t) имеет на любом конечном интервале конечное число точек разрыва.

Если ограничения на область значений выглядят достаточно естественно, то выбор в качестве управлений кусочно-непрерывных функций нуждается в пояснениях.

Наиболее реалистичное требование – управление u(t) непрерывная функция. Оно соответствует представлению о том, что управляющее воздействие, обладая определенной инертностью, не может изменяться скачком. Но такое требование оказывается весьма неудобным. Как свидетельствует анализ некоторых задач, решений в классе непрерывных функций может просто не существовать. Кроме того, анализ реальных управляемых объектов показывает, что почти всегда в качестве управляющих можно выбрать такие параметры, которые в пределах разумной точности можно считать безынерционными. Поэтому класс кусочно-непрерывных функций оказывается выгодным с теоретической точки зрения и приемлемым с точки зрения практических приложений.

Кусочно-непрерывные управления со значениями, попадающими в область управления U, будем называть допустимыми.

Чтобы указать, как именно фазовая траектория объекта определяется по выбранному управлению, нужно знать закон движения объекта, описывающий динамические свойства рассматриваемой системы. Будем предполагать, что закон движения можно записать в виде

где f(t, x, u) – известная вектор-функция, конкретный вид которой опреде-

ляется конструктивными особенностями объекта или условиями задачи, f(t, x, u) = (f1(t, x, u), f2(t, x, u), …, fn(t, x, u))т. Далее будем полагать, что

функции fi (t, x, u) для любых i = 1, ..., n непрерывны по всей совокупности переменных и непрерывно дифференцируемы по совокупности переменных х для любого t на отрезке t0 ≤ t ≤ Т . При этих условиях могут быть до-

138

казаны существование и единственность решения уравнений (1) с заданными начальными условиями х(t0) = x0.

Решение системы уравнений движения (5.10) при заданном управлении u(t) называют фазовой траекторией, соответствующей этому управле-

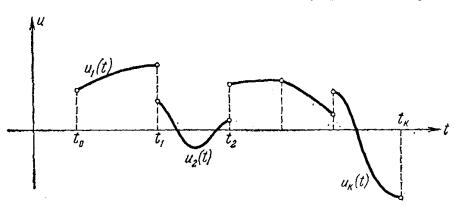
нию. Точку х(t0) = x0 будем называть левым концом траектории, а точку х(Т) – правым концом траектории. В точках разрыва какой-либо из функций управления надо производить стыковку решений системы (5.10), обеспечивающих непрерывность фазовой траектории. На рис. 5.5 показан пример, когда движение на плоскости сопровождается управлением, имею-

щим разрывы в моменты t1, t2, …, tk–1.

непрерывна на рассматриваемом отрезке времени.

Перейдем теперь к непосредственной формулировке задачи оптимального управления. Пусть в пространстве Rn заданы многообразия S0(t),

139

Такое управление u* (t) будем называть оптимальным управлением, x* (t) = x(t, u* ) , t0 ≤ t ≤ Т – оптимальной траекторией, а пару u* (t), x* (t) –

оптимальным решением рассматриваемой задачи.

Можно пользоваться более краткой формулировкой задачи оптимального управления: найти минимум функционала

с учетом того, что u(t) выбирается из класса кусочно-непрерывных или ог-

раниченных измеримых функций.

Множество G(t) называют ограничением на фазовые координаты x = (x1, x2 , ..., xn ) или просто фазовыми ограничениями. В случае

G(t) ≡ Rn при всех t [t0 ,Т] , задача (5.11)–(5.14) называется задачей оптимального управления без ограничений на фазовые координаты и условие x(t) G(t) в (5.13) не пишется. Если же G(t) ≠ Rn , то задачу (5.11)–(5.14)

называют задачей оптимального управления с ограничением на фазовые координаты.

Многообразие S0 (t) или S1(t) может не зависеть от времени и состо-

ять из одной точки, тогда говорят, что в задаче (5.11)–(5.14) левый (или соответственно правый) конец закреплен. Если же S0 (t) или S1(t) при

t0 ≤ t ≤ Т совпадает со всем пространством Rn, то говорят, что левый (или

соответственно правый) конец свободный и в этом случае условие x(t0 ) S0 (t0 ), ( x(Т) S1(Т) ) в (5.13) не пишется. Наконец, если S0 (t) или

140