книги / Теория автоматического управления. Дискретные системы

Переход от Wp′′(p) к преобразованной передаточной функции дискретной системы Wp′′( jλ) может быть выполнен путем разложе-

ния на простые дроби и использования таблиц типовых преобразований Лапласа. Эта задача значительно проще преобразования полной передаточной функции, так как выражение (4.38) проще исходного (4.36).

Если передаточная функция непрерывной части цифровой системы при D(z)=1, у которой коэффициенты преобразователей приведены к непрерывной части, и непрерывная часть не содержит колебательных звеньев, может быть использован приближенный

метод ограничений:

i=1

где Ti (T1 , T2 , …, Tq ) – большие постоянные времени, соответствуют сопрягающим частотам, меньшим 2/T, и малые постоянные времени Ti (Tq+1 , Tq+2 , …, Tn ), соответствующие сопрягающим

частотам, большим 2/T, а постоянным времени τ1, τ2 , …, τm соот-

ветствуют сопрягающие частоты, меньшие частоты 2/T. Если вертикальная прямая ω=2/T пересекается асимптотой ЛАПЧХ с наклоном –20 дБ/дек, комплексная псевдочастотная функция имеет вид

n

где TΣ = ∑Ti .

i=q+1

71

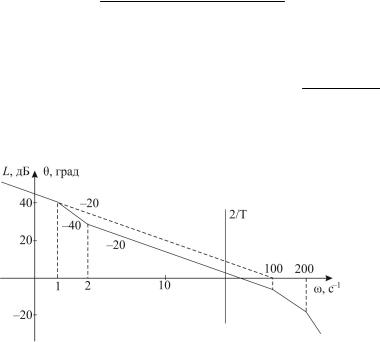
При пересечении вертикальной линии ω=2/T ЛАПЧХ непрерывной части системы с наклоном –40 дБ/дек комплексная псевдочастотная функция описывается

i=1

Пример 4.4. Построить логарифмические псевдочастотные характеристики (ЛПЧХ) дискретной системы с периодом квантования T=0,05 с и экстраполятором нулевого порядка, если передаточная функция непрерывной части имеет вид

100(0,5 p+1)

W ( p)= p( p+1)(0,01p+1)(0,005 p+1).

На рис. 4.12 приведена ЛАЧХ непрерывной части системы, на которой выделена область низких частот, разделенная частотой

ω=2/T =40 рад/c, с передаточной функцией Wн ( p)=100(0,5 p+1) p( p+1)

и суммарным значением малых постоянных времени

TΣ =0,01+0,005=0,015 c.

Рис. 4.12. ЛАЧХ непрерывной части системы

72

По (4.40) получим выражение комплексной псевдочастотной функции:

Рис. 4.13. ЛПЧХ дискретнойсистемы кпримеру4.4

На основании этого выражения на рис. 4.13 построены ЛПЧХ дискретной системы. Логарифмическая фазовая псевдочастотная характеристика имеет уравнение, составляющие которого отмечены на рис. 4.13 номерами 1–6.

Θ(λ)=−π/ 2−arctgλ+arctg0,5λ−2arctgλ0,025+arctgλ0,001.

Как видно по результатам, применение метода ограничений существенно упрощает построение ЛПЧХ дискретных систем со сложной структурой непрерывной части.

73

5. АНАЛИЗ ДИСКРЕТНЫХ СИСТЕМ УПРАВЛЕНИЯ

Исследование дискретных систем начинается с оценки их принципиальной работоспособности, т.е. устойчивости. В классе линейных дискретных систем исследование ведется так же, как и в теории линейных непрерывных САУ, но с учетом особенностей, связанных с квантованием сигналов, и соответственно специфики математического аппарата их описания. Известно, что устойчивость непрерывных линейных систем определяется по переходной составляющей решения однородного дифференциального уравнения системы. Аналогично решается задача и для дискретных систем.

Если линейное неоднородное разностное уравнение дискретной системы имеет вид

то общее решение однородного разностного уравнения (f[n]=0) при некратных корнях характеристического уравнения может быть записано как

а Сi – произвольные постоянные.

Из (5.2) вытекает, чтобы свободное движение дискретной системы, описываемой разностным уравнением (5.1), т.е. переходная составляющая была затухающей (lim y[n]n→∞=0), необходимо выполнение условия

Для разностного уравнения в векторной форме устойчивость общего решения однородного уравнения определяется по собственным числам zi матрицы А, вычисленным как корни уравнения det(zI–A)=0.

Аналогичное решение получаем при решении уравнения дискретной системы, заданной в виде дискретной передаточной функции.

74

Итак, на основании полученного условия (5.4) формулируется

корневой критерий устойчивости: «Для того чтобы дискретная САУ была устойчива, необходимо и достаточно, чтобы модули корней характеристического уравнения системы были меньше 1».

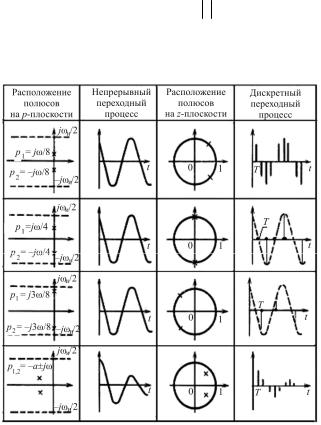
Если характеристическое уравнение системы получено из уравнения системы в форме D-преобразования Лапласа, его корни для устойчивой системы должны располагаться в левой полуполосе p-плос- кости или в левой полуплоскости псевдочастот w. Плоскости корней р

и z связаны преобразованием z =epT =e(σ+jω)T =eσT e jωT , и при комплексных корнях р на z-плоскости имеем z =eσT и arg z =ωT.

На рис. 5.1 приведено расположение корней характеристического уравнения дискретной системы второго порядка (полюсов передаточной функции) на p- и z-плоскостях.

Рис. 5.1. Расположение полюсов передаточной функции системы 2-го порядка на p- и z-плоскостях (см. также с. 76)

75

Рис. 5.1. Окончание

Так, например, если в характеристическом уравнении имеется пара комплексных сопряженных корней, расположенных на окружности единичного радиуса, то имеет место колебательная граница устойчивости. В этом случае с течением времени в системе устанавливаются незатухающие периодические колебания.

Если имеются полюсы на окружности единичного радиуса ( zi =1), а все остальные – внутри круга, то цифровая система на-

ходится на границе устойчивости. Если это полюс zi =+1, то цифровая система называется нейтральной.

76

Дискретная система будет находиться на апериодической границе устойчивости, если в ее характеристическом уравнении (5.3) имеется корень zi =1, а остальные корни располагаются внутри

круга единичного радиуса. В этом случае переходная составляющая решения разностного уравнения с течением времени стремится к значению Ci .

Наличию в характеристическом уравнении корня zi =−1 со-

ответствуют незатухающие колебания с периодом, равным 2Т. Таким образом, для определения устойчивости требуется оп-

ределить, все ли корни характеристического уравнения располагаются внутри единичной окружности, причем желательно это выполнить без вычисления их значений.

Дискретные системы второго и даже первого порядка, в отличие от непрерывных систем такого же порядка, могут быть неустойчивыми даже при положительных коэффициентах характеристического уравнения. Это может быть вызвано снижением частоты квантования непрерывного сигнала, что приводит к увеличению вносимого в систему экстраполятором запаздывания

(см. рис. 1.9).

Пример 5.1. Рассмотрим условие устойчивости дискретной системы, структурная схема которой приведена на рис. 3.1. Объект системы описывается передаточной функцией интегрирующего звена, фиксатор представлен экстраполятором нулевого порядка.

Передаточная функция разомкнутой системы в форме z-пре-

образования будет Wp (z)= zkT−и1.

Из передаточной функции замкнутой системы получим характеристическое уравнение системы вида z – 1+kTи=0, откуда условие устойчивости будет |z|=(1 – kTи)<1.

Таким образом, период квантования в заданной дискретной системе должен быть Tи<2/k.

77

В инженерной практике как для непрерывных, так и дискретных систем для оценки устойчивости используются алгебраические

ичастотные критерии.

5.1.Алгебраические критерии устойчивости

5.1.1. Критерий устойчивости Гурвица

Выполним в характеристическом уравнении дискретной сис-

темы замену z =11+−ww. В результате получим характеристический

полином D(w), по которому определим устойчивость системы.

Как уже было показано в главе 4, окружность единичного радиуса в плоскости z, как и отрезок мнимой оси на плоскости p, преобразуется в мнимую ось w-плоскости, и полюсы передаточной

плексная переменная w движется по оси мнимых чисел от –j∞ до +j∞. Внутренняя часть круга единичного радиуса z-плоскости отображается при этом на левую полуплоскость w-плоскости.

Исследование дискретных систем по преобразованным при помощи w-преобразования передаточным функциям проводится по критерию Гурвица в порядке, используемом для непрерывных систем.

Пусть замкнутая дискретная система имеет характеристическое уравнение

Выполнив замену переменной z на w, получим новое уравнение:

a0 (1+w)n +a1(1+w)n−1 (1−w)+...+an (1−w)n =0;

78

Согласно критерию Гурвица необходимым и достаточным условием устойчивости является положительность всех диагональных миноров определителя Гурвица, составленных из коэффициентов уравнения (5.6) при положительном коэффициенте при старшей степени w.

Критерий Гурвица оказывается, как и применительно к непрерывным системам, громоздким для исследования систем высоких порядков.

5.1.2. Критерий устойчивости Шура – Кона

Если характеристическое уравнение имеет высокий порядок, целесообразно использовать алгебраический критерий по оценке расположения корней zi характеристического уравнения внутри единичной окружности. Для применения данного критерия из коэффициентов характеристического уравнения (5.5) дискретной системы в замкнутом состоянии, заданного в форме Z-преобразования, составляется таблица:

Для устойчивости замкнутой дискретной системы необходимо и достаточно, чтобы все расчетные коэффициенты λi (i=1,2,…,n) первого столбца таблицы были по модулю меньше единицы.

Критерий Шура – Кона имеет большое преимущество перед другими критериями при использовании ЭВМ для анализа систем высоких порядков.

79

5.2. Частотные критерии устойчивости

5.2.1. Критерий устойчивости Михайлова

Доказательство критерия устойчивости Михайлова дискретных систем, как и для непрерывных систем, основано на применении принципа аргумента.

Пусть известно характеристическое уравнение замкнутой дискретной системы в форме(5.5). Представим его через сомножители:

где zi – корни уравнения (5.5).

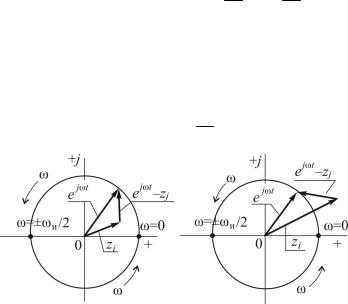
Полагая z = ejωT найдем изменение аргумента разностного вектора (ejωT – zi) одного из сомножителей, входящих в характеристи-

ческое уравнение, при изменении ω от −ω2и до +ω2и .

Если корень характеристического уравнения располагается внутри круга единичного радиуса, как показано на рис. 5.2, a, то ∆arg(e jωT −zi )=2π, при его расположении вне круга – ∆arg(e jωT −zi )=0 (рис. 5.2, б). Поворот вектора А(z)=0 для поло-

жительного диапазона частот 0<ω<ω2и вдвое меньше.

аб

Рис. 5.2. К оценке поворота векторов (ejωT – zi)

80