Дерево и лес

Граф G называется деревом если он является связным и не имеет циклов.

Граф G называется лесом если все его компоненты связности - деревья.

Вершина v графа называется концевой, если её степень p( v)=1.

Ребро, инцидентное концевой вершине, называется концевым ребром.

Пусть v – вершина дерева G с корнем v 0(V) – множество всех вершин, связанных с корнем цепями, проходящими через вершину v. Это множество порождает подграф G(v), называемый ветвью вершины.

Свойства деревьев:

Следующие утверждения эквивалентны:

1) Граф G есть дерево.

2) Граф G является связным и не имеет простых циклов.

3) Граф G является связным и число его ребер ровно на 1 меньше числа вершин.

4)  две различные вершины графа G можно соединить единственной (и при этом простой) цепью.

5) Граф G не содержит циклов, но, добавляя к нему любое новое ребро, получаем ровно один и притом простой цикл

Утверждение 4. Если у дерева G имеется, по крайней мере, 1 ребро, то у него найдется висячая вершина.

Утверждение 5.Пусть G связный граф, а − висячая вершина вG, граф получается изG в результате удаления вершины и инцидентного ей ребра. Тогдатоже является связным.

Утверждение 6.Пусть G - дерево с n(G) вершинами и m(G) ребрами. Тогда m(G)=n(G)-1.

Утверждение 7.Пусть G – дерево. Тогда любая цепь в G будет простой.

Остовным деревом связного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом.

Пусть G – связный граф. Тогда остовное дерево графа G должно содержать n(G)-1 ребер. Значит, для получения остовного дерева из графа G нужно удалить ребер.

Число −цикломатическое число графа G.

Пример решения типовой задачи

Пример 1. Пусть граф типа дерева – G7 на рис. 20. Сколько вершин максимального типа имеется в данном гра­фе? Каково цикломатическое число графа? Чему равно цикломатическое число графа G ', являющегося лесом и пред­ставленного двумя одинаковыми деревьями G7. Построить ориентированное дерево с корнем v0, являющимся верши­ной максимального типа.

Типы вершин графа G7 отмечены на рис.22, а, граф содержит две вершины максимального (4-го) типа.

Цикломатическое число любого дерева v(G) = vc+ve-vv= 0.

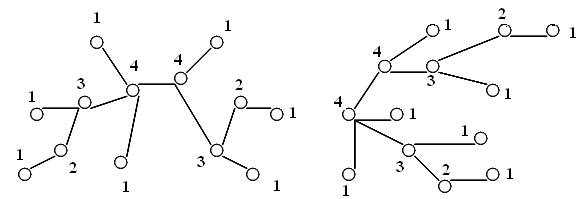
Рис. 22

Действительно, число вершин vv в дереве на едини­цу больше числа ребер ve, т.е. ve-vv= -1, а число связных компонент графа типа дерева vс= 1. Таким обра­зом, цикломатическое число любого дерева, в том числе гра­фа G7, v = 0.

Цикломатическое число леса равно сумме цикломатических чисел своих связных компонент - деревьев, т.е. также равно нулю; таким образом,

v(G ') = v(G) + v(G) = 0, где G ' -граф, представленный двумя одинаковыми дере­вьями G.

Упражнения

1. Выполнить задание примера 1 для графов, изображен­ных на рис. 23.

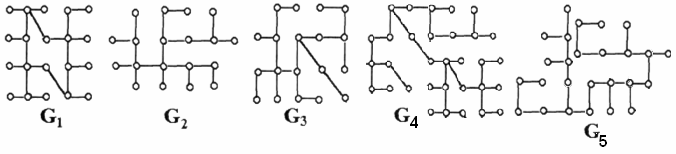
Рис. 2

2. Определить цикломатическое число и максимальный тип вершин.

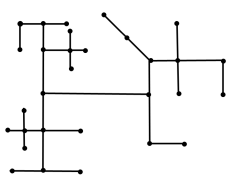
3. Найти остов минимального веса.

2 4 3 5 2 3 6 1

4. Найдите количество остовных подграфов, являющихся деревьями, в полных подграфах с 3-мя, 4-мя, 5-ю, 6-ю вершинами.

5. Нарисовать все попарно неизоморфные деревья восьмого порядка.

6. Доказать, что центр дерева состоит из 1 вершины в случае, когда диаметр этого дерева четное число, и из 2-х смежный вершин, если диаметр – нечетное число.

7. Нарисовать все попарно неизоморфные деревья седьмого порядка.

8. Докажите, что если из каждой вершины графа выходит более одного ребра, то граф не является деревом.

9. Докажите, что у дерева всегда найдется вершина, из которой выходит ровно одно ребро. (Такая вершина называется висячей)

10. Докажите, что если у графа-дерева удалить висячую вершину вместе с ребром, из нее выходящим, то полученный граф снова будет деревом.

11. На конференции присутствуют 50 ученых, каждый из которых знаком, по крайней мере, с 25 участниками конференции. Докажите, что найдутся четверо из них, которых можно усадить за круглый стол так, чтобы каждый сидел рядом со знакомыми ему людьми.

12. В некоторой стране любые два города соединены либо авиалинией, либо железной дорогой. Докажите, что а) можно выбрать вид транспорта так, чтобы от любого города можно было добраться до любого другого, пользуясь только этим видом транспорта;

б) из некоторого города, выбрав один из видов транспорта, можно добраться до любого другого города не более, чем с одной пересадкой (пользоваться можно только выбранным видом транспорта) в) можно выбрать вид транспорта так, чтобы пользуясь только им, можно было добраться из любого города до любого другого не более, чем с двумя пересадками.

13. Дима, приехав из Врунляндии, рассказал, что там есть несколько озер, соединенных между собой реками. Из каждого озера вытекают три реки, и в каждое озеро впадают четыре реки. Докажите, что он ошибается.

14. В некоторой стране есть столица и еще 100 городов. Некоторые города (в том числе и столица) соединены дорогами с односторонним движением. Из каждого нестоличного города выходит 20 дорог, и в каждый город входит 21 дорога. Докажите, что в столицу нельзя проехать ни из одного города.

15. В некотором городе каждый город соединен с каждым дорогой. Сумасшедший король хочет ввести на дорогах одностороннее движение так, чтобы выехав из любого города, в него нельзя было вернуться. Можно ли так сделать?

16. Докажите, что на ребрах связного графа можно расставить стрелки так, чтобы из некоторой вершины можно было добраться по стрелкам до любой другой.

17. В связном графе степени всех вершин четны. Докажите, что на ребрах этого графа можно расставить стрелки так, чтобы выполнялись следующие условия: а) двигаясь по стрелкам, можно добраться от любой вершины до любой другой; б) для каждой вершины числа входящих и исходящих ребер равны.

18. В одном государстве 100 городов и каждый соединен с каждым дорогой с односторонним движением. Докажите, что можно поменять направление движения на одной дороге так, чтобы от любого города можно было доехать до любого другого.