4. Метод сведения матричной игры к задаче линейного программирования.

Рассмотрим универсальный метод решения матричных игр, позволяющий в принципе исследовать игру любой размерности.

Пусть имеется игра mхn без седловой точки и без доминируемых стратегий, заданная матрицей

.

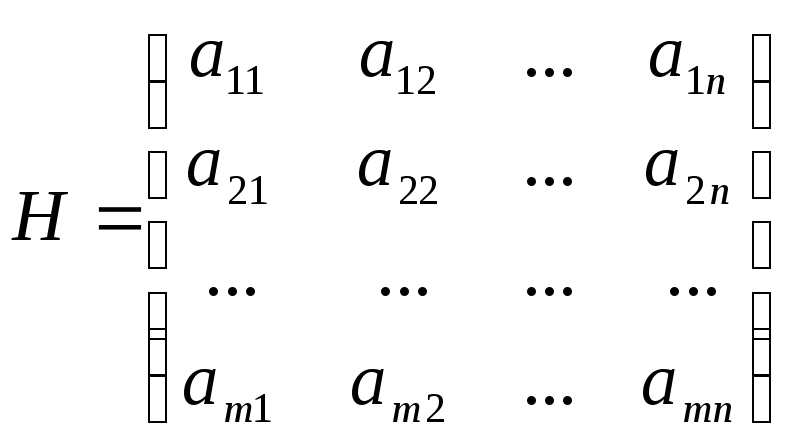Априорно допустим, что цена этой игры положительна. Это значение заранее неизвестно, но, согласно свойству 2 из п.2.2, v_S, где  - нижняя цена игры. Так что при 0 условие v_S0 выполнено. Если же 0, то выполнение такого условия можно гарантировать, прибавив, например, ко всем элементам матрицы Н число с и получив матрицу Н новой игры. Согласно свойству 1 из п. 2.2, новая игра имеет то же самое решение, что и исходная игра, а ее цена v_S'=v_S+c.

Итак, пусть v_S0. Мы хотим найти две оптимальные смешанные стратегии S_A*=(р₁,…,р_m) и S_B*=(р₁,…,р_n), дающие каждому игроку максимально возможные для него средние выигрыши. Найдем S_A*. Уже известно, что, если игрок А применяет свою оптимальную стратегию, то игрок В не может улучшить свое положение, отступая от своей оптимальной стратегии: H(S_A*,S_B)H(S_A*,S_B*)=v_S для всех S_B (проигрыш В будет не меньше, чем v_S). В частности, если игрок В пользуется какой-либо чистой стратегией В_j, то:

H(S_A*,B_j)=a_1jp₁+…+a_mjp_mv_S при всех j=1,…,n.

Получим следующую систему неравенств:

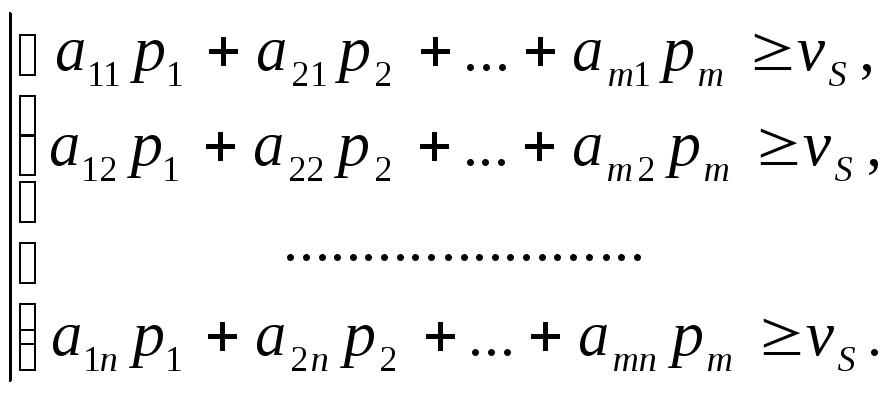(2.8)

Так как v_S0, то при почленном делении левых и правых частей неравенств (2.8) на v_S знаки неравенств не изменятся. Вводя, кроме того, обозначения x_j=p_j/v_S, перепишем систему (2.8) в виде:

(2.9)

Условие р₁+р₂+…+р_m=1 равносильно условию x₁+x₂+…+x_m=1/v_S.

Но v_S – гарантированный выигрыш игрока А. Целью игрока А в игре является максимизация этого значения и, следовательно, минимизация выражения 1/v_S. Получили следующую задачу линейного программирования:

Найти неотрицательные значения x₁, x₂,…, x_m, которые удовлетворяют линейным ограничениям – неравенствам (2.9) и обращают в минимум целевую функцию L=x₁+x₂+…+x_m.

Полученная задача может быть решена, например, симплекс-методом. Пусть (x₁*,x₂*,…,x_m*) - некоторое решение этой задачи, L* - минимальное значение целевой функции L . Тогда цена игры v_S=1/L*, а компоненты оптимальной стратегии игрока А равны: p_j*=x_j*/L* (j=1,…,m).

Оптимальная стратегия игрока В находится аналогично. В результате приходим к задаче линейного программирования, двойственной к первой:

y₁+y₂+…+y_n  max

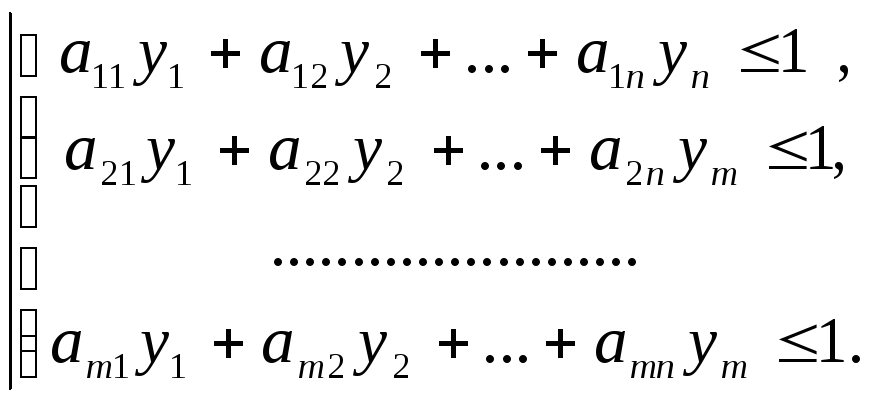(2.10)

Решение (y₁*,y₂*,…,y_n*) этой задачи и компоненты q₁*,q₂*,…,q_n* оптимальной стратегии игрока В связаны соотношениями: q_i*=y_i*/L*, где L* - максимальное значение целевой функции задачи (2.10), совпадающее с минимальным значением предыдущей задачи.

Пример 2.7. Найти решение игры, заданной матрицей

.

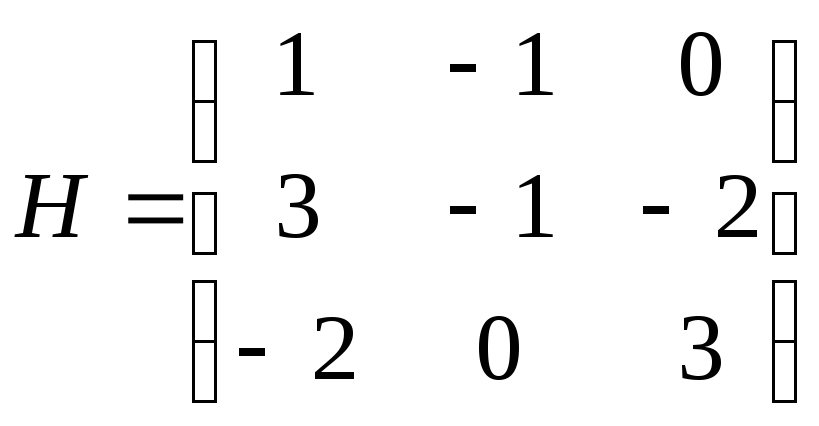Во-первых, заметим, что данная игра не имеет доминируемых стратегий, так что сокращение размерности матрицы невозможно. Далее проверим, не имеет ли матрица седловую точку. Найдем нижнюю и верхнюю цены игры:

, . Так как , то седловая точка отсутствует. Приступаем к поиску решения игры в смешанных стратегиях, используя метод сведения игры к задаче линейного программирования.

Прибавим ко всем элементам матрицы Н модуль ее наименьшего отрицательного элемента, т. е. 2. Получим матрицу

,

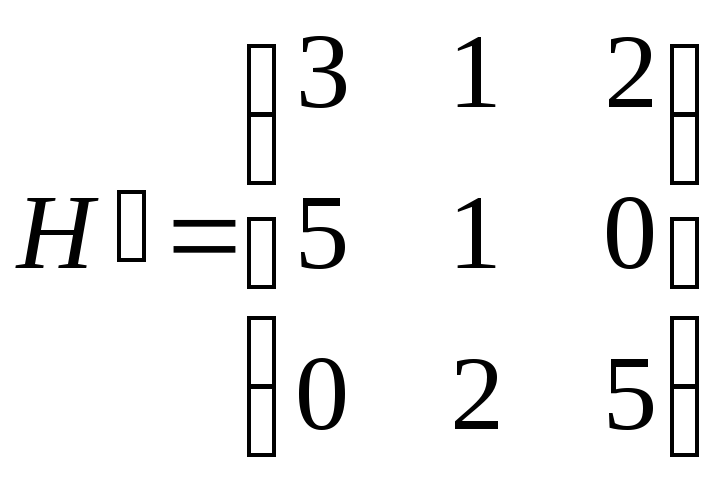которая задает игру с заведомо положительной ценой v_S. Для нахождения оптимальной смешанной стратегии игрока А составим следующую задачу линейного программирования:

L =x₁+x₂+x₃  min

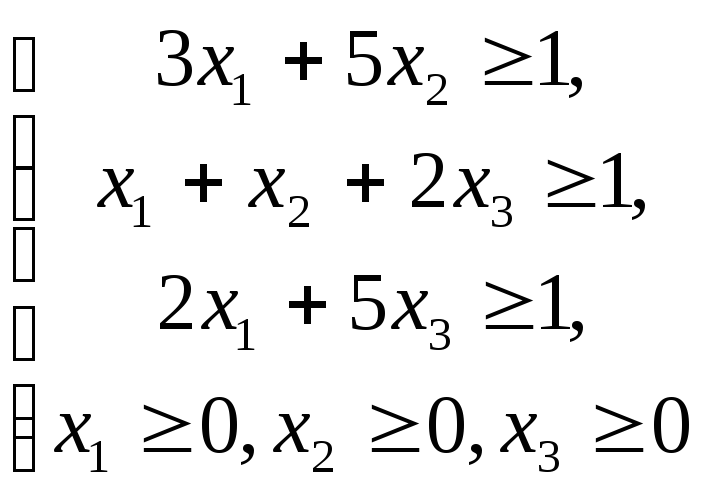(2.11)

Для нахождения оптимальной стратегии игрока В составим двойственную задачу:

L₁=y₁+y₂+y₃  max

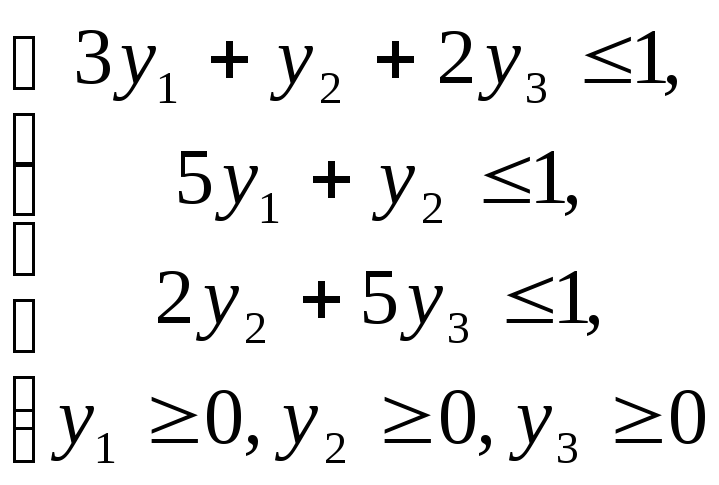(2.12)

Симплекс-методом удобнее решать задачу (2.12). Опуская процесс расчетов этим методом, запишем лишь результат: у₁*=1/4, у₂*=5/4, у₃*=0 – решение задачи (2.12), максимальное значение целевой функции L₁*=3/2. Отсюда находим компоненты оптимальной смешанной стратегии игрока В: q₁*=(1/4):(3/2)=1/6, q₂*=(5/4):(3/2)=5/6, q₃*=0; цена игры v_S=1/L₁*. При решении задачи линейного программирования симплекс-методом в итоговой симплекс-таблице содержится также и решение двойственной задачи, в нашем случае - задачи (2.11): х₁*=0, х₂*=1/2, х₃*=1. Учитывая, что L*=L₁*, отсюда получим: p₁*=0:(3/2)=0, p₂*=(1/2):(3/2)=1/3, p₃*=1:(3/2)=2/3. Согласно свойству 1 решения матричных игр (п.2.3), оптимальные смешанные стратегии исходной игры совпадают с найденными оптимальными стратегиями: S_A*=(0,1/3,2/3), S_B*=(1/6,5/6,0). Цена v_S исходной игры и найденная цена v_S вспомогательной игры связаны соотношением v_S=v_S+2. Поэтому v_S=2/32=4/3.